八校联合体第一次联考
高二年级 数学试卷
第Ⅰ卷 (选择题 共50分)
一、选择题:本大题共10小题,每小题5分,共50分,在下列各题给出的四个选项中,只有一项是符合要求的。
1、 下列不等式恒成立的是()
A.![]() B.
B. ![]() C.
C.
![]() D.若
D.若![]() ,则
,则![]()
2、椭圆![]() 的准线方程是()
的准线方程是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
|
|
|
|
|
|
|
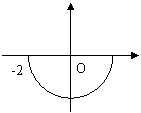 B.
B. 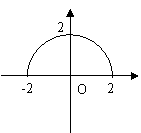
|
|
|
|
|
|
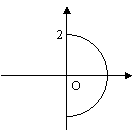 D.
D.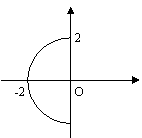
4、若![]() 是直线的倾斜角,则
是直线的倾斜角,则![]() 值属于()
值属于()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
5、直线![]() 与两坐标轴围成的面积是()
与两坐标轴围成的面积是()
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
6、两条直线![]() ,
,![]() 垂直的充要条件是()
垂直的充要条件是()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7、已知直线![]() 与
与![]() 的斜率是方程
的斜率是方程![]() 的两个根,则
的两个根,则![]() 与
与![]() 的夹角为()
的夹角为()
A. ![]() B.
B.![]() C.
C.
![]() D.
D.
![]()
8、过点![]() ,且圆心在直线
,且圆心在直线![]() 上的圆方程是()
上的圆方程是()
A. ![]() B.
B.![]()
C.![]() D.
D.![]()
9、已知平面上三点![]() ,目标函数
,目标函数![]() 的可行域是四边形
的可行域是四边形![]() (包括边界但不包括坐标原点
(包括边界但不包括坐标原点![]() )。若
)。若![]() 为该目标函数的唯一的最优解,则实数
为该目标函数的唯一的最优解,则实数![]() 的范围是()
的范围是()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10、已知△![]() 的三个顶点都在椭圆
的三个顶点都在椭圆![]() 上,且
上,且![]() 两点关于原点
两点关于原点![]() 对称,设直线
对称,设直线![]() 的斜率为
的斜率为![]() ,直线
,直线![]() 的斜率为
的斜率为![]() ,则
,则![]() 的值为()
的值为()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
第Ⅱ卷 (非选择卷 共100分)
二、填空题:本大题共6小题,每小题4分,共24分。
11、不等式![]() 的解集是_______________;
的解集是_______________;
12、点![]() 到直线
到直线![]() 的距离是_____________;
的距离是_____________;
13、若椭圆![]() 的离心率为
的离心率为![]() ,则
,则![]() ______________;
______________;
14、设满足![]() 的点
的点![]() 的集合为
的集合为![]() ,满足
,满足![]() 的点
的点![]() 的集合为
的集合为![]() ,其中
,其中![]() 是正数,且
是正数,且![]() ,则
,则![]() 满足的关系是_______________;
满足的关系是_______________;
15、![]() ,
,![]() ,
,![]() 为椭圆
为椭圆![]() 上三点,若
上三点,若![]() 与
与![]() 三点的距离成等差数列,则
三点的距离成等差数列,则![]() __________________;
__________________;
16、在下面等号右侧两分数线下的分母位置方块中各填上一个自然数,使等式成立且这两个自然数的和最小:![]() 。
。
三、解答题:(本大题满分76分)本大题共有6题,解答下列各题必须写出必要的步骤。
17、(本题满分12分)解下列不等式:
(1)![]() ;
(2)
;
(2)![]() 。
。
18、(本题满分12分)若![]() ,求证:
,求证:![]() 。
。
19、(本题满分12分)过![]() 作两互相垂直的直线
作两互相垂直的直线![]() 和
和![]() ,
,![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 与
与![]() 轴交于
轴交于![]() ,求线段
,求线段![]() 中点
中点![]() 的轨迹方程。
的轨迹方程。
20、(本题满分12分)过点![]() 作圆
作圆![]() 的两条切线,切点分别为
的两条切线,切点分别为![]() 。
。
求(1)经过圆心![]() ,切点
,切点![]() 这三点圆的方程;
这三点圆的方程;
(2)直线![]() 的方程;
的方程;
(3)线段![]() 的长。
的长。
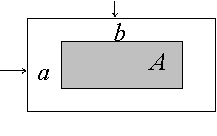
21、(本题满分14分)某种印刷品,单面印刷,其版面(如图阴影部分)排成矩形,版面面积为![]() ,它的左、右两边都要留宽为
,它的左、右两边都要留宽为![]() 的空白,上、下两边都要留宽为
的空白,上、下两边都要留宽为![]() 的空白,且印刷品左、右长度不超过定值
的空白,且印刷品左、右长度不超过定值![]() 。问如何选择纸张的尺寸(纸张也是矩形),才能使每一张印刷品所用纸张面积最小,从而使印刷品的总用纸量最少?
。问如何选择纸张的尺寸(纸张也是矩形),才能使每一张印刷品所用纸张面积最小,从而使印刷品的总用纸量最少?
22、(本题满分14分)如图,已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,一条经过点
轴上,一条经过点![]() ,且方向向量为
,且方向向量为![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,又
点,又![]() 。
。
(1)
求直线![]() 的方程;
的方程;
(2)
求椭圆![]() 长轴长的取值范围。
长轴长的取值范围。