高中学生学科素质训练
高二数学同步测试(3)—不等式综合
共150分,考试用时120分钟。
一、选择题(本大题共10小题,每小题5分,共50分)
1.已知a、b、c满足![]() ,且
,且![]() ,那么下列选项中不一定成立的 ( )
,那么下列选项中不一定成立的 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.不等式![]() 的解集是
( )
的解集是
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.若![]() 则下列结论中不正确的是 ( )
则下列结论中不正确的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.设![]() 则以下不等式中不恒成立的是 ( )
则以下不等式中不恒成立的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.对于![]() ,给出下列四个不等式
( )
,给出下列四个不等式
( )
①![]() ②
②![]()
③![]() ④
④![]()
其中成立的是 ( )
A.①与③ B.①与④ C.②与③ D.②与④
6.设![]() 的最值情况是 ( )
的最值情况是 ( )
A.有最大值2,最小值![]() B.有最大值2,最小值0
B.有最大值2,最小值0
C.有最大值10,最小值![]() D.最值不存在
D.最值不存在
7.![]() 的最小值 ( )
的最小值 ( )
A.![]() -
-![]() B.
B.![]() -
-![]() C.-
C.-![]() -
-![]() D.
D.![]() +
+![]()
8.已知0<a<b<1,则a b 、log b a 、![]() 的大小关系是 ( )
的大小关系是 ( )
A.![]() B.
B.![]()
C.log ba<![]() D.ab<
D.ab<![]()
9.下列命题中,(1)![]() 的最小值是2,(2)
的最小值是2,(2)![]() 的最小值是2,(3)
的最小值是2,(3)![]() 的最
的最
小值是2,(4)![]() 的最小值2,正确的有 ( )
的最小值2,正确的有 ( )
A.1个 B.2个 C.3个 D.4个
10.设![]() 若0<x·y<1 , 0<x+y<1+xy , 则x ,y满足条件 ( )
若0<x·y<1 , 0<x+y<1+xy , 则x ,y满足条件 ( )
A.x >1 , y>1 B.0<x<1 , 0<y<
二、填空题(本大题共5小题,每小题4分,共20分)
11.已知![]() 则不等式
则不等式![]() 的解集是
.
的解集是
.
12.若![]() ,则函数
,则函数![]() 的最小值是 ________.
的最小值是 ________.
13.某市用37辆汽车往灾区运送一批救灾物资,假设以![]() 公里/小时的速度匀速直达灾区,已知某市到灾区公路线长400公里,为了安全起见,两辆汽车的间距不得小于
公里/小时的速度匀速直达灾区,已知某市到灾区公路线长400公里,为了安全起见,两辆汽车的间距不得小于![]() 公里,那么这批物资全部到达灾区的最少时间是________________小时.(车身长不计)
公里,那么这批物资全部到达灾区的最少时间是________________小时.(车身长不计)
14.实数已知两个正数x,y满足x+y=4,则使不等式![]() ≥m,恒成立的实数m的取值范围是
≥m,恒成立的实数m的取值范围是
15.方程![]() 又一正根一负根,则实数
又一正根一负根,则实数![]() 的取值范围是
.
的取值范围是
.
三、解答题(本大题共7小题,共80分。解答应写出文字说明,证明过程或演算步骤)
16.(10分)解关于x的不等式![]() ,其中 a>0且
,其中 a>0且![]()
17.(10分)当 sin2x>0 时,求: 不等式 log 0.5(x2-2x-15)>log 0.5(x+13) 的解集。
18.(12分)已知![]() 且x2 + y2 ≤1, 求:
且x2 + y2 ≤1, 求:![]() 的范围。
的范围。
19.(12分)已知![]() 且-4
且-4![]() 的取值范围。
的取值范围。
20.(12分)已知a > 0, b < 0 ,且a2 + b2 <1,设P = ![]() 试比较
试比较
P,Q的大小并说明理由。
21.(10分)刹车距离是分析事故的一个重要因素。在一个限速40千米/小时以内的弯道上,甲、乙两辆汽车相向而行,发现情况不对,同时刹车,但还是碰了。事发后现场测得甲车的刹车距离略超过
s甲=0.1x+0.01x2
s乙=0.05x+0.005x2
问超速行驶应负主要责任的是谁.
22.(14分)已知条件![]() 和条件
和条件![]() ,请选取适当的实数
,请选取适当的实数![]() 的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题.则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
的值,分别利用所给的两个条件作为A、B构造命题:“若A则B”,并使得构造的原命题为真命题,而其逆命题为假命题.则这样的一个原命题可以是什么?并说明为什么这一命题是符合要求的命题.
参 考 答 案(3)
一、选择题(每小题5分,共50分):
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| C | A | D | B | D | A | B | A | A | B |
8.答:A
要点:∵ 0 < a <1 ∴![]() ∴
∴![]() ,∵0<a <b <1,
,∵0<a <b <1,
∴0< ab<
1 , log b a>log b b =1 , ∴log![]() ,
,
应选A
9.答:A
要点:当![]() 的最小值是2,
的最小值是2,
(2)正确,当![]() 所以
所以![]()
取不到最小值2,故(3)错误,当![]() 错误,所以选A
错误,所以选A
10.答案:B
分析:由0<xy<1可知x 、y同号,且有x+y>0可知x ,y同正。
又1+xy<x+y有(1-x)(1-y)>0 ,可知x>1 且y>1或x<1且y<1 ,
又0<xy<1 ,可知0<x<1 ,0<y<1.
二、填空题(每小题4分,共20分)
11.![]() 12.
12.![]() 13.12 14.
13.12 14.![]() 15.
15.![]()
三、解答题(共80分,按步骤得分)
16.(10分)答:原不等式解集为![]()
要点:原不等式可化为![]()
![]()
(1)若![]() 则
则![]() 于是由(1)得
于是由(1)得![]() ,即有
,即有![]()
(1)若![]() ,则
,则![]() 于是由(2)得
于是由(2)得![]() 即有
即有![]()
综全(1)、(2)得原不等式解集为![]()
17.(10分)答案:![]()
要点:由sin2x>0 得 ![]() ①
①
不等式![]()
等价于不等式组
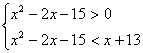
解为![]() ② 由 ①,② 可得:略
② 由 ①,② 可得:略
18.(12分)答:![]()
要点![]()
![]() ,
, ![]()
1)若x+y≥0 , 则
![]()
![]()
2)若x+y<0 ,则
![]() 。
。
综上得:![]()
19.(12分)答:![]()
要点:![]() 解得
解得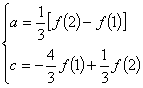
![]()
![]() 则
则![]() 又
又![]()
![]() ,
, ![]()
即![]()
20.(12分)答:![]()
要点:![]()
![]() ①
①
同理由0 < b2 < a2 + b2 < 1
得-lgb2>-lg![]() >0
②
>0
②
①×②得![]()
21.(10分)分析:要弄清主要责任者,就需分析行驶速度,要弄清速度问题,就要运用刹
车距离函数和实测数据,构建一元二次不等式。
略解:由题意列出不等式
s甲=0.1x+0.01x2>12
s乙=0.05x+0.005x2>10
这是常见的一元二次不等式,分别求解,得
x<-40或x>30
x<-50或x>40
由于x>0,从而可得,x甲>
经比较知乙车超过限速,应负主要责任。
注:解实际应用题首先要正确理解题意,恰当地进行数学化设计,化归为课本中的标准化模型加以解决。
22.(14分) [分析] 本题为一开放性命题,由于能得到的答案不唯一,使得本题的求解没有固定的模式,考生既能在一般性的推导中找到一个满足条件的![]() ,也能先猜后证,所找到的实数
,也能先猜后证,所找到的实数![]() 只需满足
只需满足![]() ,且
,且![]() 1即可.这种新颖的命题形式有较强的综合性,同时也是对于四个命题考查的一种新尝试,如此命题可以考查学生探究问题、解决问题的能力,符合当今倡导研究性学习的教学方向.
1即可.这种新颖的命题形式有较强的综合性,同时也是对于四个命题考查的一种新尝试,如此命题可以考查学生探究问题、解决问题的能力,符合当今倡导研究性学习的教学方向.
[解答] 已知条件![]() 即
即![]() ,或
,或![]() ,∴
,∴![]() ,或
,或![]() ,
,
已知条件![]() 即
即![]() ,∴
,∴![]() ,或
,或![]() ;
;
令![]() ,则
,则![]() 即
即![]() ,或
,或![]() ,此时必有
,此时必有![]() 成立,反之不然.
成立,反之不然.
故可以选取的一个实数是![]() ,A为
,A为![]() ,B为
,B为![]() ,对应的命题是若
,对应的命题是若![]() 则
则![]() ,
,
由以上过程可知这一命题的原命题为真命题,但它的逆命题为假命题.