高二数学测试题—直线和平面的位置关系（2）

高中学生学科素质训练

高二数学测试题—直线和平面的位置关系（2）

一、选择题：（本大题共10小题，每小题5分，共50分）

1．已知直线　　　　　（　　）

　　　 A．异面　　　　　　　　　 B．相交　　　　　　　　　 C．平行　　　　　　　　　 D．不确定

2．过空间一点作平面，使其同时与两条异面直线平行，这样的平面　　　　　　　　　　　 （　　）

　　　 A．只有一个　　　　　　　　　　　　　　　　　　　　　 B．至多有两个　　　　

　　　 C．不一定有　　　　　　　　　　　　　　　　　　　　　 D．有无数个

3．如果直角三角形的斜边与平面平行，两条直角边所在直线与平面所成的角分别为，则　　　　　　　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A．　　　　　　　　　　　　 B．

　　　 C．　　　　　　　　　　　　 D．

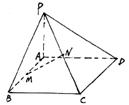
4．设E、F、G分别是四面体的棱BC、CD、DA的中点，则此四面体中与过E、F、G的截面平行的棱有　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．0条　　　　　　　　　　B．1条　　　　　　　　　　C．2条　　　　　　　　　　D．3条

5．用表示一个平面，l表示一条直线，则平面内至少有一条直线与l　　　　　　　 （　　）

　　　 A．平行　　　　　　　　　 B．相交　　　　　　　　　 C．异面　　　　　　　　　 D．垂直

6．如图Rt△ABC中，∠ACB=90°，直线l过点A且垂直于平面ABC，动点P∈l，当点P逐渐远离点A时，∠PCB的大小 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．变大　　　　　　　　　

　　　 B．变小　　　　　　　　　

　　　 C．不变　　　　　　　　　

　　　 D．有时变大有时变小

7．设a,b是平面外的任意两条线段，则“a，b的长相等”是a,b在平面内的射影长相等”的　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．充分条件　　　　　　　　　　　　　　　　　　　　　 B．必要条件　　　　　　

　　　 C．充要条件　　　　　　　　　　　　　　　　　　　　　 D．既非充分也非必要条件

8．设PA，PB，PC是从点P引出的三条射线，每两条的夹角都等于60°，则直线PC与平面APB所成角的余弦值是　　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）

　　　 A．　　　　　　　　　　　B．　　　　　　　　　 C．　　　　　　　　　 D．

9．已知△ABC中，AB=9，AC=15，∠BAC=120°，△ABC所在平面外一点P到此三角形三个顶点的距离都是14，则点P到平面ABC的距离是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（　　）

　　　 A．7　　　　　　　　　　　　B．9　　　　　　　　　　　　C．11　　　　　　　　　　　 D．13

10．已知a,b,c,d是四条不重合的直线，其中c为a在平面上的射影，d为b在平面上的射影，则　　　　　　　 　　　　　　　　　　　　　　　　（　　）

　　　 A．a∥da∥b　　　 B．a⊥bc⊥d　　　 C．a∥bc∥d　　　 D．c⊥da⊥b

二、填空题（本大题共4小题，每小题6分，共24分）

11．平面外的一侧有一个三角形，三个顶点到的距离分别是7，9，13。则这个三角形的重心到的距离为 　　　　　　　　　　  .

12．已知矩形ABCD中，AB=1，BC=a，PA⊥平面ABCD。若在BC上有且仅有一个点Q，满足PQ⊥QD，则a的值为 　　　　　　　　　　  .

13．空间一个角的两边分别垂直于另一角的两边是这两个角相等或互补的 　　　　  条件.

14．在正方体AC₁中，过顶点A及另两个顶点且与该正方体的12条棱所在直线成相等的角的平面是 　　　　　　　　　　  （将所有可能结果都填上）.

三、解答题（本大题共6题，共76分）

15．已知PA⊥矩形ABCD所在平面，M、N分别是AB、PC的中点.

（1）求证：MN⊥CD；

（2）若∠PDA=45°，求证MN⊥面PCD.(12分)

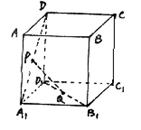
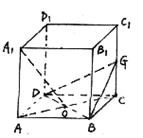
16．设P、Q是单位正方体AC₁的面AA₁D₁D、面A₁B₁C₁D₁的中心。

　　　 如图：（1）证明：PQ∥平面AA₁B₁B；

　　　 （2）求线段PQ的长。（12分）

17．如图，已知

　　　 求证a∥l（12分）

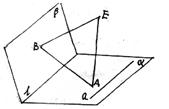
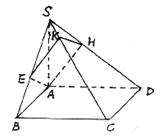
18．如图，ABCD为正方形，过A作线段SA⊥面ABCD，又过A作与SC垂直的平面交SB、SC、SD于E、K、H，求证：E、H分别是点A在直线SB和SD上的射影。（12分）

19．在正方体ABCD—A₁B₁C₁D₁，G为CC₁的中点，O为底面ABCD的中心。

　　　 求证：A₁O⊥平面GBD（14分）

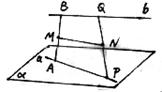
20．如图，已知a、b是两条相互垂直的异面直线，其公垂线段AB的长为定值m，定长为n（n>m）的线段PQ的两个端点分别在a、b上移动，M、N分别是AB、PQ的中点。

　　　 （1）求证：AB⊥MN；

　　　 （2）求证：MN的长是定值（14分）

高二数学参考答案

（二）直线和平面的位置关系

一、选择题

1．C　2．C　3．B　4．C　5．D　6．C　7．D　8．C　9．A　10．C

二、填空题

11．　　 12．2　　13．既非充分又非必要　　14．平面AD₁B₁或平面ACD₁。

三、解答题（本题考查证明线线垂直、线面垂直的基本方法）

15．证明：

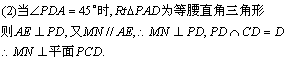
16．（本题考查证明线面平行的方法）

评注：本题提供了两种解法，方法一，通过平行四边形的对边平行得到“线线平行”，从而证得“线面平行”；方法二，通过三角形的中位线与底边平行得到“线线平行”，从而证得“线面平行”。本题证法较多。

17．证明：

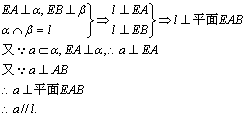
18．证明：

19．证明：

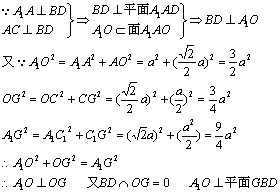
20．证明：