钱库第二高级中学数学期末考试试卷3
班级： 姓名：
一. 选择题(每小题3分,共30分)
1.不等式
的解集为( )
A.
B.
C.
D.
2.已知
,那么( )
A.
B. 
C. 
D. 
3. 直线
的倾斜角为
,则
的值是( )
A.
B. 
C.
D. 
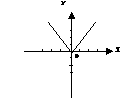
4. 方程
所表示的曲线为( )
 | |||||||
 |  |  | |||||
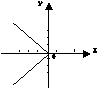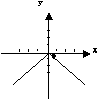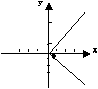A. B. C. D.
5. (文科学生做)已知
,则函数
有( )
A.最大值
B.最小值 C. 最大值 
D. 最小值
(理科学生做)
已知
,则函数有( )
A.最小值 B.最大值 C. 最小值 D. 最大值
6. 直线
的方向向量为
,直线
的方向向量为
,那么到的角是( )
A.
B.
C. 
D.
7. 若
,则下列不等式一定成立的是( )
A.
B. 
C. 
D. 
8. 直线
绕它与
轴的交点逆时针旋转
,所得到的直线方程是( )
A. 
B.
C. 
D.
9. 设
,
(
),则
的大小关系是( ) A.
B. 
C. 
D.不能确定
10. 方程
只有负数解,那么实数取值范围为( )
A. B.
C.
D.
二. 填空题(每小题4分,共24分)
11. 直线
和
互相垂直,则 
.
12. 动点
分别在直线
和
上移动,则线段
中点
的轨迹方程为 ．
13. (文科学生做)已知
且
,则
的最小值为_________.
(理科学生做) 已知
,且
,则
的最大值为_________.
14. (文科学生做)不等式
的解集为_______________.
(理科学生做)定义符号函数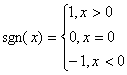
,则不等式
的解集为_______________.
15.直线
与
满足∥,且原点
到
距离相等,则
.
16. 若实数
同时满足下列四个条件:1)
;2)
;3)
;
4) 
.则下列判断中正确的是_______________.(将正确判断的序号都填上)
①
;②
;③
;④
;⑤
.
三. 解答题(五大题,共46分)
17.(本题8分)
解不等式
.
18. (本题8分)
求线性目标函数
的最大值,式中
满足约束条件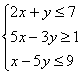
.
19. (本题10分)
直线
过点
,并且与两条直线:
围成一个锐角三角形,
求直线斜率的范围和倾斜角的范围.
20. (文科学生做,本题10分)
点
到直线
的距离为
,直线与轴,
轴正半轴分别交于点
.
(1) 求证:
;
(2) 求
面积的最小值(其中为坐标原点).
(理科学生做,本题12分)点到直线
的距离为,且原点与点
在的同侧,直线与轴,轴正半轴分别交于点.
(1)求证:,且
;
(3) 求面积的最小值.
21. (文科学生做本题10分)
已知
,且
,判断
与的大小关系并证明.
(理科学生做,本题8分)
已知,且
, 判断
与
的大小关系并证明.
参考答案
一.选择题
1.A, 2.D 3.A 4.B 5.A 6.B 7.D 8.C 9.Ｃ 10.B
二.填空题
11.
; 12.
; 13.文64；理1；
14.文
，理
； 15.
; 16.①④⑤
三.解答题
17.移项通分得:
,-------------------------------------4分
由序轴标根法知
.------------------4分
18. 画出可行域(图略)---------------------------------------3分
求出最优解(4,-1),---------------------------------------3分
得
.----------------------------------------------2分
19. 
直线的斜率
,
的角
满足
, 为钝角;-------------- 3分
又点在直线的上方,只需
的角
和
的角
都是锐角;
; 的斜率
满足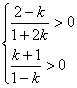
,----------------------- 3分
解得
,--------------------------------------------------------------2分
的倾斜角范围为
.---------------------------------2分
20. (1)(文) 直线的方程可化为
------------------------ 1分
由点到直线的距离为1知: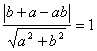 
---------------------1分;
整理(过程略)得:------------------------------------ 2分
(理)上述过程相同;
设
,原点与点在直线的同侧,
而
,
即
------------------------------ 1分;
由
知:
,------------------------------------ 1分
假设
,则必有
;
由知:
且
,矛盾,(答略)--2分
(2)由(1)得
,----------------------------(文3分理2分)
解得
,
---------------------(文3分理2分)
21. (文) 判断结果:
------------------------------------- 4分
设
,则
,
;--3分
又
,
;
即.-------------------------------3分
(理) 判断结果: 
-------------------------------2分
设
,则
;
---3分
又,
,
即.-------------------------3分