福田中学2004~2005学年第二学期期末考试
高二年级数学试卷
命题人：潘伟军 审查人：潘伟军
本试卷分为第Ⅰ、Ⅱ卷两部分，满分100分，考试时间100分钟。
第Ⅰ卷
一、选择题：本大题共10小题，每小题4分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．
1、1．已知直线a、b、c满足a//b，b^c，则a与c的关系是………………( )
(A) 垂直 (B) 平行 (C)相交 (D) 异面
2、．22004除以7的余数是………………( )
(A) 1 (B) 2 (C)5 (D) 6
3、已知
互相垂直，则k=…………( )
(A) 1
(B) -2
(C) 
(D)
4、边长为1的正方形ABCB，沿对角线AC折成直二面角后，B、D两点间的距离为( )
(A) 2 (B)
(C) 1
(D) 
5、若( x2-2x+3)n=a2nx2n+a2n-1x2n-1 +…+a1x+a0,则a2n+a2n-2 +…+a4+a2+a0= ( )
(A)2n
(B)3n
(C)
(6n+2n) (D)(6n-2n)
6、两个球的体积之比为8：27，则它们的表面积的比是 ( )
(A) 2：3 (B) 4：9 (C)
(D) 
7、给出下列两个问题与相应的抽样方法：（1）某小区有600个家庭，其中高收入家庭100户，中等收入家庭380户，低收入家庭120户，为了了解有关家用轿车购买力的某个指标，要从中抽取一个容量为100户的样本。
（2）从15名同学中抽取3个参加座谈会。Ⅰ 简单随机抽样方法；Ⅱ 系统抽样方法；Ⅲ 分层抽样方法。问题和方法配对正确的是（ ）
(A)（1）Ⅰ（2）Ⅱ (B)（1）Ⅲ（2）Ⅰ (C)（1）Ⅱ（2）Ⅲ (D)（1）Ⅲ（2）Ⅱ
8、已知的分布列如下：且设
，则
的期望值是（ ）
|
| --1 | 0 | 1 |
| P | |
| |
(A)
(B)4
(C) -1
(D)1
9、将一个各个面上均涂有颜色的正方体锯成27个同样大小的小正方体，从这些小正方体中任取1个，其中恰有2面涂有颜色的概率为
(A)
(B)
(C)
(D)
10、已知直线l ^平面a，直线mÌ平面b，有下列四个命题:
①a//bÞ l ^m；②a^bÞ l //m；③l //mÞa^b；④l ^mÞa//b.
其中正确的命题是………………………………………………………( )
(A) ①② (B) ②④ (C) ③④ (D) ①③
二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．
11、设随机变量
服从二项分布
则
______。
12、
，以为OA、OB一组邻边作平行四边形OACB，则四边形OACB是_________、且
。
13、某年全国足球甲级（A组）联赛共有14个队，每队都要与其余各队在主、客场分别比赛1次，则共进行的比赛场数为________________。
14、三棱锥的底面是两条直角边长分别为
三、解答题
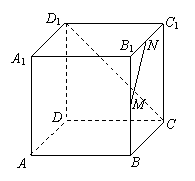15、(本题满分6分) 已知M、N分别是棱长为1的正方体ABCD－A1B
16、(本题满分7分)
（1）第6项； （2） 第3项的系数； （3）常数项。
17、(本题满分6分) 用0、1、2、3、4、5这六个数字，
组成没有重复数字的六位数。
（1）这样的六位奇数有多少个？
（2）数字5不在个位的六位数共有多少个？
（3）数字1和2不相邻，这样的六位数共有多少个？
18、(本题满分9分)
甲在与乙进行乒乓球单打比赛时获胜的概率都是
.甲与乙比赛3次，通过计算（要求写出计算过程）填写下表：
| 甲获胜次数ξ | 0 | 1 | 2 | 3 |
| 相应的概率P |
19、（本小题满分8分）
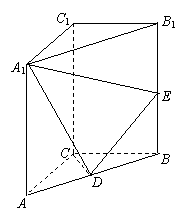如图，直三棱柱
中，
，
，
为
的中点，
点在
上，且
.
（Ⅰ）求证：
；
（Ⅱ）求二面角
的大小.
20、（本小题满分8分）
设{an
} 是正数组成的数列，其前n项和为Sn，，所有的正整数n ，满足
（1）求a1、 a2 、a3 ；
（2） 猜想数列{an }的通项公式，并用数学归纳法证明。
参考答案
一、选择题：A A D C C B B A D D
二、填空题：本大题共4小题，每小题4分，共16分．把答案填在题中横线上．
11、
12、菱形; 60º 13、182， 14、
15、解：（Ⅰ）以D为原点，DA、DC、DD1分别为x、y、z轴建立如图的空间直角坐标系.则
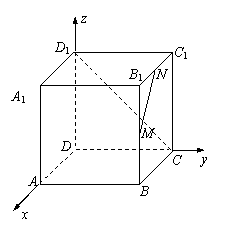A（1，0，0），B（1，1，0），C（0，1，0），D（0，0，0），
A1（1，0，1），B1（1，1，1），C1（0，1，1），D1（0，0，1），
由于M、N分别是BB1和B
M（1，1，
），N（，1，1）.
从而
=（－，0，），
＝（0，－1，1）， ………………………4分
由
＝
＝
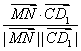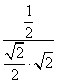＝. ……………………5分
故MN与CD1所成的角
； …………………………………6分
16、解：（1）
----2分
(2)
-----4分
（3）
-----5分
令18-3r=0 得r=6 ---6 分
即常数项为
----7分
17、解：（1）
-------2分
（2）
---------4分
（3）
--------6分
18、解：在甲与乙进行的乒乓球单打比赛中，甲获胜的概率为，则乙获胜的概率为
.
则ξ＝0，表示在3次比赛中，甲没有胜出，即P（ξ＝0）＝
＝
.………2分
ξ＝1，表示在3次比赛中，甲胜出1次，即P（ξ＝1）＝
＝
. ………4分
ξ＝2，表示在3次比赛中，甲胜出2次，即P（ξ＝2）＝
＝
.…………6分
ξ＝3，表示在3次比赛中，甲胜出3次，即P（ξ＝3）＝
＝
.…8分
所以甲获胜次数ξ的概率P为：
| 甲获胜次数ξ | 0 | 1 | 2 | 3 |
| 相应的概率P |
|
|
|
|
………………………………………………………………9分
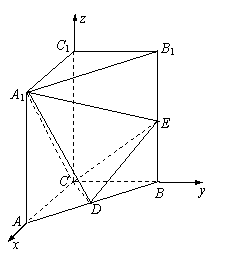
19、解法一：（Ⅰ）证明：以C为原点，CA、CB、CC1分别为x、y、z轴建立如图的空间直角坐标系.则
A（2，0，0），B（0，2，0），C（0，0，0），A1（2，0，2），B1（0，2，2），C1（0，0，2），……2分
由于
为
的中点，
点在上且.
则E（0，2，1），D（1，1，0），
从而
＝（1，1，0），
＝（－2，2，0），
＝（0，0，2）， ……………………………3分
∵ ·＝0，·＝0，且AB∩AA1＝A，
∴ 
. ……………………4分
（Ⅱ）解：由（Ⅰ）可知＝（1，1，0）是平面A1ED的法向量，
设n＝（x，y，z）是平面A1EC的法向量，
则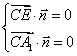
，
即
，取x＝2，则n＝（2，1，－2），………………………………6分
又
＝
＝
＝
.……………………………………7分
故二面角的大小为
.…………………………………………………8分
解法二：（Ⅰ）证：依题意知
，
且 为的中点，则 也为
中点，
∴ 
， ……………………………………………………………………1分
又∵三棱柱为直三棱柱
∴
又 
且 
、
故 . ………………………………………………………………4分
（Ⅱ）解：由1）知，在
中过作
交
于
，
连
，由三垂线定理有
为所求二面角得平面角 ………………………5分
易知
，在
中，
，
，
故
，
在
中 
故所求二面角的大小为. …………………………………………………………8分
20、解：（1）
------1分
再
--------2分
同样可得
----------3分
（2）猜想
----------4分
下面用数学归纳法证明。
10 当n=1时，结论成立；
20 假设n=k时，结论成立，即
。
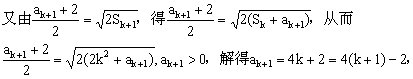
即当n=k+1时，结论也成立，--------------7分
根据10、20 对于一切正整数n都有成立。----------8分