福州市八县协作校2005—2006学年第一学期半期联考
高二年级数学试卷
【完卷时间：120分钟； 满分：150分】
命题人：黎华高（长乐七中） 校对人：黄玉惠（长乐七中）
一、单选题（本大题共12小题，每小题5分，共60分）
1. 若a<0，b>0，且a+b<0，则下列不等式中成立的是（ ）
A. －b<a<b<－a B. －b<a<－a<b
C. a<－b<b<－a D. a<－b<－a<b
2. 
（ ）
A. 150° B. 120° C. 60° D. －60°
3．如果a、b是满足不等式ab<0的实数，那么（ ）
A. a+b>a－b B. a+b<a－b
C. a－b<a－b D. a－b<a+b
4. 直线
: 
互相垂直，则
的值为（ ）
5．
（ ）
A．必要不充分条件 B．充分不必要条件
C．充要条件 D．既不充分也不必要条件
6．A点关于直线8x+6y=25的对称点恰为坐标原点，则A点的坐标为（ ）
A．(2, 
) B．
C．(3, 4) D．(4, 3)
7．下列各式中，最小值为2的是（ ）
A．
B．
C．tanx＋cotx D．
8．若
为圆
的弦AB的中点，则直线AB的方程是
（ ）
A.
B.
C.
D.
9．某杂志若每册定价
元可以发行12万份，当定价每提高
元，发行量减少4万册，每降价元，发行量增加4万册，要使总收入不低于20万元，则该杂志的最高定价应为（ ）
A.
B.
C.1元 D.2元
10．使x－4+x－5＜a有实数解的a为（ ）
A．a＞0 B．1＜a＜9 C．a＞1 D．a≥1
11．直线x – 2y +2 = 0与直线3x – y + 7 = 0的夹角等于 ( )
A．
B．
C．
. D．arctan7.
12．方程
和
（
）所确定曲线有两个交点，则的取值范围是（ ）
A．
B．
C．
D．且
二、填空题（本大题共4小题，每小题4分，共16分）
13．已知
，则
的取值范围是
14．不论
取何实数，直线
恒过定点
15.不等式
的解集为
16．已知
的两个顶点
，第三个顶点
在曲线
上移动，则的重心
的轨迹方程是
三、解答题（本大题共6小题，共74分）
17．（本小题满分12分）
解关于x的不等式
18．(本小题满分12分)
已知过点P（1，4）的直线
在两坐标轴上的截距均为正值，当两截距之和最小时，求直线的方程。
19．(本小题满分12分)
已知a，b，c都是正数，且a，b，c成等比数列，求证：
20．(本小题满分12分)
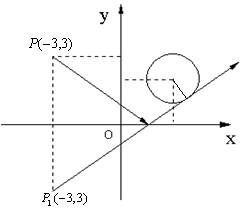
自点P（－3，3）发出的光线经过x轴反射，其反射光线所在直线正好与圆
相切，求入射光线所在直线的方程。
21．(本小题满分12分)
一玩具公司在每天工作10小时的机器上可制造两种玩具：卫兵和骑兵．如果造一个卫兵需8秒钟和8克金属，造一个骑兵需要6秒钟和16克金属，每天可供给的金属最多有64千克，若制造一个卫兵的利润为0.5元，造一个骑兵的利润为0.6元，问每种玩具造多少能使利润最大？每天最大利润是多少？
| |
 | |
| |
 |
22．(本小题满分14分)
已知n条直线：L1：x－y＋C1=0,C1
=
， L2：x－y＋C2=0，L3：x－y＋C3=0，……Ln：x－y＋Cn=0
.(其中C1< C2 <C3 <……<
Cn)这ｎ条平行线中，每相邻两条之间的距离顺次为2，3，4，……，n.
（1）求Cn ；
（2）求x－y＋Cn=0与x轴、y轴围成的图形的面积；
（3）求x－y＋Cn－1=0与x－y＋Cn=0及x轴、y轴围成的图形的面积．
福州市八县协作校2005—2006学年第一学期半期联考
高二年级数学试卷参考答案
一、单选题（本大题共12小题，每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | B | B | D | B | D | D | A | C | C | B | A |
二、填空题（本大题共4小题，每小题4分，共16分）
| 题号 | 13 | 14 | 15 | 16 |
| 答案 |
|
|
|
|
三、解答题（本大题共6小题，共74分）
17．（本小题满分12分）
解：原不等式
. 分情况讨论……………………（2分）
（i） 当a＜0或a＞1时，有a＜a2，此时不等式的解集为
…（5分）
（ii）当
时，有a2＜a，此时不等式组的解集为
…（8分）
（iii）当a=0或a=1时，原不等式无解．…………………………………（10分）
综上，当a＜0或a＞1时时，原不等式的解集为；
当
时，原不等式的解集为
当a=0或a=1时，原不等式的解集为.………………………………（12分）
18．(本小题满分12分)
…（2分）
……（6分）
………（11分）
（12分）
19．(本小题满分12分)
证明：左－右=2（ab+bc－ac）……………………（3分）
∵a，b，c成等比数列， 
……………（5分）
又∵a，b，c都是正数，所以
≤
∴
…（8分）
∴
………………………（11分）
∴
………………………………………………（12分）
20．(本小题满分12分)
解：设入射光线所在的直线方程为
，反射光线所在直线
的斜率为
，根据入射角等于反射角，得k1=－k……………………(3分)
又点P（－3，3）关于x轴的对称点
（－3，－3），根据对称性，点在反射光线所在直线上，故反射光线所在直线
的方程为：
，即
，………………………（6分）
又此直线与已知圆相切，所在圆心到直线的距离等于半径
，因为已知圆圆心为（2，2），半径为1，所以
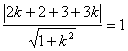解得：
………………………………………………………（10分）
故入射光线所在的直线方程为：
或
即
…………………………………（12分）
 |
21．(本小题满分12分)
解：设制造卫兵x 个，制造骑兵y个，每天总利润为z元………………（1分）
|
|
…………………………………………………（5分）
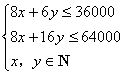
由图：
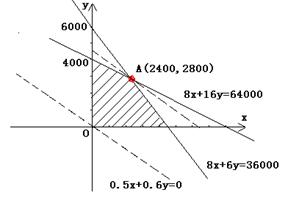
……………（9分）
解方程组
所以
（元）…………………（11分）
答：制造卫兵2400个，骑兵2800个能使每天利润达到最大值，最大值为2880元。…………………………………………………………………………（12分）
22．(本小题满分14分)
解:（1）由题意可知：L1到Ln的距离为:
=2+3+4+···+n,
∵
>∴=
．…………………………………………（4分）
（2）设直线Ln：x－y＋Cn=0交x轴于Ｍ点，交ｙ轴于Ｎ点，则△ＯＭＮ的面积为：Ｓ△ＯＭＮ＝
│ＯＭ││ＯＮ│=
=
．…………………（8分）
（3）围成的图形是等腰梯形,由(2)知Ｓｎ＝
．则有
Sｎ－１＝
Sｎ－Sｎ－１＝
－
＝ｎ３
所以所求面积为n3．…………………………………………………………（14分）