成都市新都一中高二数学(上)第七章测试题
时间:120分钟 总分150分
考生誓言:我以我的荣誉发誓,绝不给予或接受任何形式的帮助!考生姓名:
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.下列说法正确的是( )
A.![]() 是过点
是过点![]() ,且斜率为
,且斜率为![]() 的直线方程.
的直线方程.
B.在![]() 轴和
轴和![]() 轴上的截距分别为
轴上的截距分别为![]() 的直线方程为
的直线方程为![]()
C.直线![]() 与
与![]() 轴交点到原点的距离为
轴交点到原点的距离为![]()
D.不与坐标轴平行或重合的直线的方程一定可以写出两点式或斜率式.
2.方程![]() 表示的曲线,经过点
表示的曲线,经过点![]() ,
,![]() ,
,![]() ,
,![]() 中的( )
中的( )
A.0个 B.1个 C.2个 D.3个
3.过点![]() 和点
和点![]() 的直线的一般式方程是( )
的直线的一般式方程是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
|
|
5. 设直线![]() 过点
过点![]() ,且与圆
,且与圆![]() 相切,则
相切,则![]() 的斜率是( )
的斜率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.![]() :
:![]() 和
和![]() :
:![]() 的位置关系是( )
的位置关系是( )
A.相离 B.外切 C.相交 D.内切
7. 下列四个命题中真命题是( )
A.经过定点![]() 的直线都可以用方程
的直线都可以用方程![]() 表示
表示
B.经过任意两个不同的点![]() ,
,![]() 的直线都可以用方程
的直线都可以用方程![]() 表示
表示
C.不经过原点的直线都可以用方程![]() 表示
表示
D.经过定点![]() 的直线都可以用方程
的直线都可以用方程![]() 表示
表示
8. 将直线![]() 沿用
沿用![]() 轴向左平移
轴向左平移![]() 个单位,所得直线与圆
个单位,所得直线与圆![]() 相切,则实数
相切,则实数![]() 的值为( )
的值为( )
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
9. ![]() 是圆
是圆![]() 内一点,过
内一点,过![]() 点最长的弦所在的直线方程是( )
点最长的弦所在的直线方程是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
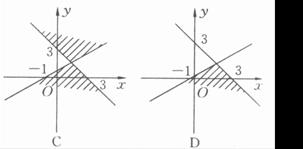
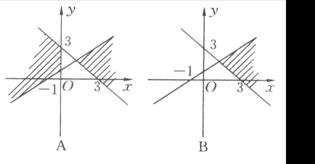
10. 已知![]() ,
,![]() 满足
满足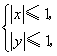 则
则![]() 的最大值为( )
的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.直线![]() 绕原点按逆时针旋转
绕原点按逆时针旋转![]() 后所得直线与圆
后所得直线与圆![]() 的位置关系是( )
的位置关系是( )
A.直线过圆心 B.直线与圆相交,但不过圆心
C.直线与圆相切 D.直线与圆没有公共点
12. 直线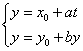 (
(![]() 为非零常数,
为非零常数,![]() 为参数)上两点
为参数)上两点![]() 对应的参数值分别为
对应的参数值分别为![]() 则
则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本大题共4小题,每小题4分,共16分,把答案填写在题中横线上.
13. 已知动点![]() 到定点
到定点![]() 的距离是
的距离是![]() 到
到![]() 的距离的
的距离的![]() 倍,则
倍,则![]() 的轨迹方程是 .
的轨迹方程是 .
14. 点![]() 到
到![]() 轴的距离是它到
轴的距离是它到![]() 轴的距离的
轴的距离的![]() 倍,则点
倍,则点![]() 的轨迹方程是 .
的轨迹方程是 .
15. 设![]() ,
,![]() 两点的坐标是
两点的坐标是![]() ,
,![]() ,若动点
,若动点![]() 满足
满足![]() ,则动点
,则动点![]() 的轨迹方程是 .
的轨迹方程是 .
16. 若直线![]() 与函数
与函数![]() (
(![]() ,且
,且![]() )的图象有两个公共点,则
)的图象有两个公共点,则![]() 的取值范围是________________.
的取值范围是________________.
三、解答题:本大题共6小题,共74分,解答应写出必要的计算过程、推演步骤或文字说明.
17.(本小题12分) 已知曲线上任一点到![]() 的距离减去它到
的距离减去它到![]() 轴的距离的差是
轴的距离的差是![]() ,求这曲线的方程.
,求这曲线的方程.
18.(本小题12分) 如图,某客运公司规定旅客可随身携带一定重量的行李,如果超过规定,则需要购买行李票,行李票费用![]() (元)与行李重量
(元)与行李重量![]() 的关系用直线
的关系用直线![]() 的方程表示,试求:
的方程表示,试求:
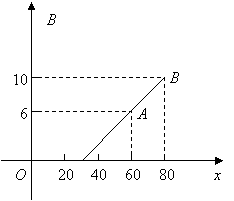 (1)直线
(1)直线![]() 的方程.
的方程.
(2)旅客最多可免费携带多少行李?
19.(本小题12分) 一动点![]() 到互相垂直平分的两条线段
到互相垂直平分的两条线段![]() 的端点的连线满足
的端点的连线满足![]() .求点
.求点![]() 的轨迹方程.
的轨迹方程.
20.(本小题12分) 点![]() ,动点
,动点![]() 满足
满足![]() ,求点
,求点![]() 的轨迹方程.
的轨迹方程.
21.(本小题14分) 已知圆![]() ,定点
,定点![]() ,问过
,问过![]() 点的直线的斜角在什么范围内取值时,这条直线与圆:(1)相切,(2)相交,(3)相离,并写出过
点的直线的斜角在什么范围内取值时,这条直线与圆:(1)相切,(2)相交,(3)相离,并写出过![]() 点的切线的方程.
点的切线的方程.
22.(本小题12分) 北京华欣公司计划在今年内同时出售夜莺牌多功能电子琴和![]() 智能型洗衣机.由于这两种产品的市场需求量大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的是资金和劳动力,通过调查,得到关于两种产品有关数据如下表:
智能型洗衣机.由于这两种产品的市场需求量大,有多少就能销售多少,因此该公司要根据实际情况(如资金、劳动力)确定产品的月供应量,以使得总利润达到最大.已知对这两种产品有直接限制的是资金和劳动力,通过调查,得到关于两种产品有关数据如下表:
| 资金 | 单位产品所需资金(百元) | 月资金供应量 (百元) | |
| 电子琴 | 洗衣机 | ||
| 成本 |
|
|
|
| 劳动力(工资) |
|
|
|
| 单位利润 |
|
| |
试问:怎样确定两种产品的月供应量,才能使总利润最大?
成都市新都一中高二数学(上)第七章测试题
一、选择题:本大题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. D 2.C 3.B 4. C 5. C 6.C 7. B 8. A 9. B 10. D 11.C 12. C
二、填空题:本大题共4小题,每小题4分,共16分,把答案填写在题中横线上.
13.
![]() . 14.
. 14. ![]() 或
或![]() .
.
15.
![]() . 16.
. 16. ![]()
三、解答题:本大题共6小题,共74分,解答应写出必要的计算过程、推演步骤或文字说明.
17.(本小题12分) 解:设![]() 为曲线上任一点,作
为曲线上任一点,作![]() 轴于点
轴于点![]() ,那么
,那么![]() ,代入坐标为
,代入坐标为![]() .
.
把等号左边![]() 项移到右边后,两边平方化简.
项移到右边后,两边平方化简.
当![]() 时,化为
时,化为![]() .
.
当![]() 时,化为
时,化为![]() .
.
故所求的曲线方程为![]() ,或
,或![]() .
.
18.(本小题12分) (1)由图知,点![]() ,
,![]() ,由直线的两点式或斜截式方程可求得直线
,由直线的两点式或斜截式方程可求得直线![]() 的方程是
的方程是![]() .
.
(2)依题意,令![]() ,得
,得![]() ,
,
即旅客最多可免费携带![]() 行李.
行李.
19.(本小题12分) 解:以![]() 所在直线为
所在直线为![]() 轴与
轴与![]() 轴,建立直角坐标系.
轴,建立直角坐标系.
设各点坐标为:![]()
设![]() 为轨迹上任意一点,则
为轨迹上任意一点,则
![]() .
.
![]() .
.
化简得:![]() .
.
20.(本小题12分) 解:如图,设点![]() .
.
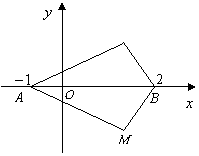 (1)当
(1)当![]() 时,设点
时,设点![]() 在
在![]() 轴或
轴或![]() 轴上方,
轴上方,
则![]() ,
,
而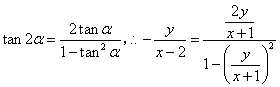 ,
,
化简得![]() ,或
,或![]() .
.
设点![]() 在
在![]() 轴下方时,
轴下方时,
则![]() ,
,
而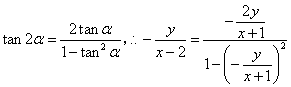 .
.
化简得![]() ,或
,或![]() .
.
![]() 总有
总有![]() ,或
,或![]() .
.
![]() ,
,
![]() 且
且![]() 为所求轨迹方程.
为所求轨迹方程.
当点![]() 在
在![]() 轴上时,如果
轴上时,如果![]() 在线段
在线段![]() 上时,满足
上时,满足![]() ,而在
,而在![]() 的延长线上或其反向延长线上时,不满足
的延长线上或其反向延长线上时,不满足![]() ,所以
,所以![]() 且
且![]() 是轨迹方程.
是轨迹方程.
(2)当![]() 时,
时,![]() 的斜率不存在,此时
的斜率不存在,此时![]() 为等腰直角三角形,点
为等腰直角三角形,点![]() 或
或![]() 经验证满足方程
经验证满足方程![]() .
.
综上,点![]() 的轨迹方程为
的轨迹方程为![]() 或
或![]() .
.
21.(本小题14分) 解:设过![]() 点的直线的倾斜角为
点的直线的倾斜角为![]() ,则其方程为
,则其方程为![]() ;
;
设圆心到直线的距离为![]() ,则
,则![]() .
.
(1)若![]() ,则
,则![]() .
.
![]() ,
,![]() 或
或![]() .
.
即当倾斜角为![]() 或
或![]() 时,直线与圆相切,切线方程为
时,直线与圆相切,切线方程为![]() 或
或![]() .
.
(2)若![]() ,即
,即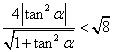 ,
,![]() ,即
,即![]() .
.
![]() 时,直线与圆相交.
时,直线与圆相交.
(3)若![]() ,即
,即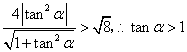 或
或![]() .
.
![]() 时,直线与圆相离.
时,直线与圆相离.
又![]() 时,直线与圆也相离,
时,直线与圆也相离,
![]() 时,直线与圆相离.
时,直线与圆相离.
22.(本小题12分) 解:设电子琴和洗衣机的月供应量分别为![]() 架、
架、![]() 台,总利润为
台,总利润为![]() 百元,由题意得
百元,由题意得
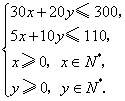 即
即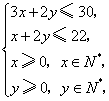 且
且![]() .
.
作出不等式组表示的区域即可行域即可行域(图略).
作直线![]() ,即
,即![]() ,
,
直线过可行域内![]() 和
和![]() 的交点时,直线纵截距最大,从而对应出
的交点时,直线纵截距最大,从而对应出![]() 最大.
最大.
解方程组![]() 得
得![]()
![]() 的坐标为
的坐标为![]() ,
,
![]() 当月供应量为电子琴
当月供应量为电子琴![]() 架、洗衣机
架、洗衣机![]() 台时,该店可获得最大利润,
台时,该店可获得最大利润,
最大利润为![]() (百元).
(百元).