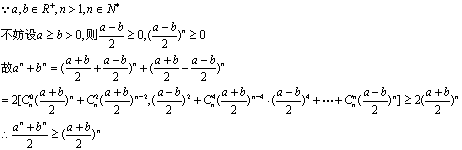高中学生学科素质训练
高二数学测试题—排列、组合、二项式定理（6）
一、选择题：（本大题共10小题，每小题5分，共50分）
1．n∈N*，则（20-n）(21-n)……(100-n)等于 （ ）
A．
B．
C．
D．
2．若集合
是从M到N的映射，则满足
的映射有 （ ）
A．6个 B．7个
C．8个 D．9个
3．有三张卡片，正反面分别写有6个不同的数字1，3，5和2，4，6，将这三张卡片上的数字排成三位数，共能组成不同的三位数的个数是 （ ）
A．24 B．36
C．48 D．64
4．（1-x）2n-1展开式中，二项式系数最大的项是 （ ）
A．第n-1项 B．第n项
C．第n-1项与第n+1项 D．第n项与第n+1项
5．设有编号为1，2，3，4，5的五个茶杯和编号为1，2，3，4，5的五个杯盖，将五个杯盖盖在五个茶杯上，至少有两个杯盖和茶杯的编号相同的盖法有 （ ）
A．30种 B．31种
C．32种 D．36种
6．从6名学生中，选出4人分别从事A、B、C、D四项不同的工作，若其中，甲、乙两人不能从事工作A，则不同的选派方案共有 （ ）
A．96种 B．180种
C．240种 D．280种
7．书架上有不同的数学书与不同的外文书共7本，现取2本数学书，1本外文书借给3位同学，每人一本，共有72种不同的借法，则数学书与外文书的本数分别为 （ ）
A．4，3 B．3，4
C．5，2 D．2，5
8．
的展开式中，无理数项的个数是 （ ）
A．84 B．85
C．86 D．87
9．4名男生3名女生排成一排，若3名女生中有2名站在一起，但3名女生不能全排在一起，则不同的排法种数有 （ ）
A．2880 B．3080
C．3200 D．3600
10．从1，2，3，4，5这五个数字中，任取三个组成无重复数字的三位数，但当三个数字中有2和3时，2需排在3前面（不一定相邻），这样的三位数有 （ ）
A．9个 B．15个
C．42个 D．51个
二、填空题（本大题共4小题，每小题6分，共24分）
11．已知
.
12．把13个乒乓球运动员分成3组，一组5人，另两组各4人，但3个种子选手每组要选派1人，则不同的分法有 种.
13．
的值的个位数是
.
14．在1到100这100个自然数中，选取20个，要求这20个数两两不相邻，则共有
种选法.
三、解答题（本大题共6题，共76分）
15．已知
的展开式中含xn项的系数相等，求实数m的取值范围.(12分)
16．一个口袋内有4个不同的红球，6个不同的白球，
（1）从中任取4个球，红球的个数不比白球少的取法有多少种？
（2）若取一个红球记2分，取一个白球记1分，从中任取5个球，使总分不少于7分的取法有多少种？（12分）
17．3名老师带领6名学生平均分成三个小组到三个工厂进行社会调查，每小组有1名老师和2名学生组成，求不同的分配方法有多少种？（12分）
18．求（2x-1）5的展开式中（1）各项系数之和；（2）各项的二项式系数之和；（3）偶数项的二项式系数之和；（4）各项系数的绝对值之和；（5）奇次项系数之和（12分）
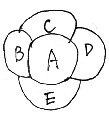
19．某市A有四个郊县B、C、D、E。（如图）
|
20．已知：
求证：
（14分）
高二数学参考答案
（六）排列、组合、二项式定理
一、选择题
1．C 2．B 3．C 4．D 5．B 6．C 7．B 8．A 9．A 10．D
二、填空题11．47
12．12600种 提示：
13．7
14．
三、解答题
15．解：
16．解（1）将取出4个球分成三类情况1）取4个红球，没有白球，有
种 2）取3个红球1个白球，有
种；3）取2个红球2个白球，有
17．解：分三步1）将6名学生平均分成三组有
.
2）将3名老师分到三组之中有
种
3）将3个不同的组分配到三个不同的工厂，有种 由分步计数原理得：
种.
18．解
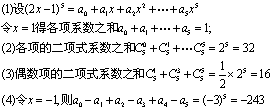
19．解：符合题意的涂色至少要3种颜色，分类如下
20．证明
