2005学年第二学期期中杭州地区七校联考试卷
高二年级数学学科
总分100分
一、选择题(本大题共10小题,每小题3分,共30分。在每小题给出的四个选项中,只有一项是符合题目要求的。)
1.分别在两相交平面内的两条直线的位置关系有
A.相交 B.相交或平行
C.相交或异面 D.相交或平行或异面
2.已知![]() 垂直于正方形
垂直于正方形![]() 所在平面,则下列等式中不成立的是
所在平面,则下列等式中不成立的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.已知直线![]() 与平面
与平面![]() 成
成![]() 角,直线
角,直线![]() ,若直线
,若直线![]() 在
在![]() 内的射影与直线
内的射影与直线![]() 也成
也成![]() 角,则
角,则![]() 与
与![]() 所成角是
所成角是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.下列命题是真命题的是
A.若直线![]() 都平行于平面
都平行于平面![]() ,则
,则![]() ;
;
B.设![]() 是直二面角,若
是直二面角,若![]() ,则
,则![]() ;
;
C.若直线![]() 在平面
在平面![]() 内的射影依次是一个点和一条直线,且
内的射影依次是一个点和一条直线,且![]() ,则
,则![]() 在
在![]() 内或
内或![]() 与
与![]() 平行;
平行;
D.若直线![]() 是异面直线,若
是异面直线,若![]() 与平面
与平面![]() 平行,则
平行,则![]() 与
与![]() 相交。
相交。
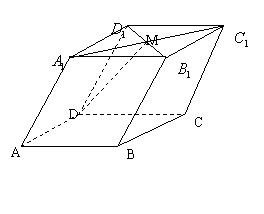 5.如图,在平行六面体
5.如图,在平行六面体![]() 中,
中,![]() 为
为![]() 的交点。若
的交点。若![]() ,则下列向量中与
,则下列向量中与![]() 相等的向量是
相等的向量是
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.已知![]() 则以
则以![]() 为邻边的平行四边形的面积为
为邻边的平行四边形的面积为
A.![]() B.
B.![]() C.4 D.8
C.4 D.8
7.平行六面体![]() 的六个面都是菱形,则顶点
的六个面都是菱形,则顶点![]() 在平面
在平面![]() 上的射影一定是
上的射影一定是![]() 的
的
A.重心 B.外心 C.内心 D.垂心
8.正方体![]() 的棱长为
的棱长为![]() ,
, ![]() 是棱
是棱![]() 的中点,则点
的中点,则点![]() 到直线
到直线![]() 的距离是
的距离是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9. 棱锥的底面是正方形,一条侧棱垂直于底面,不通过此棱的一个侧面与底面所成的二面角为![]() ,且最长的侧棱长为
,且最长的侧棱长为![]() ,则棱锥的高为
,则棱锥的高为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.一个四面体的某一顶点上的三条棱两两互相垂直,其长均为![]() ,且四面体的四个顶点在同一球面上,则此球的表面积为
,且四面体的四个顶点在同一球面上,则此球的表面积为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(本大题共5小题,每小题4分,共20分。)
11.对空间任一点![]() 和不共线的三点
和不共线的三点![]() 之间满足向量关系式
之间满足向量关系式![]() ,当点
,当点![]() 与
与![]() 共面时,则
共面时,则![]() =
。
=
。
12.已知点A、B和平面![]() 的距离分别是40和70,P为线段AB内一点,且
的距离分别是40和70,P为线段AB内一点,且![]() ,则点P到平面
,则点P到平面![]() 的距离是
。
的距离是
。
13.在北纬![]() 圈上有甲、乙两地,它们的经度差为
圈上有甲、乙两地,它们的经度差为![]() ,设地球半径为R,则甲、乙两地的球面距离是
。
,设地球半径为R,则甲、乙两地的球面距离是
。
14.![]() 是两个不同的平面,
是两个不同的平面,![]() 是平面
是平面![]() 及
及![]() 之外的两条不同直线,给出四个论断:①
之外的两条不同直线,给出四个论断:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,以其中三个论断作为条件,余下一个作为结论,写出你认为正确的一个命题:
。(注:写出一个即可。)
,以其中三个论断作为条件,余下一个作为结论,写出你认为正确的一个命题:
。(注:写出一个即可。)
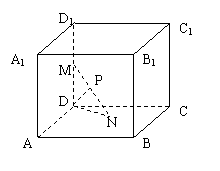 15.已知每条棱长都为3的直平行六面体
15.已知每条棱长都为3的直平行六面体![]() 中,
中,![]() ,
,
长为2的线段![]() 的一个端点
的一个端点![]() 在
在![]() 上
上
运动,另一个端点![]() 在底面
在底面![]() 上运动,
上运动,
则![]() 中点
中点![]() 的轨迹与直平行六面体的面
的轨迹与直平行六面体的面
所围成的几何体的体积为 。
三、解答题(本大题共4小题,共50分)
16.(本小题满分12分)
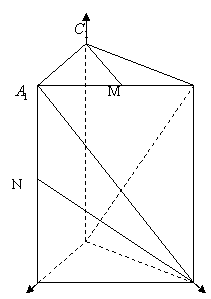
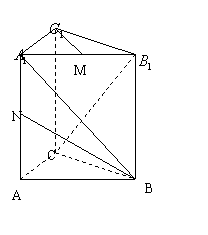 在直三棱柱
在直三棱柱![]() 中,
中,![]() ,棱
,棱![]() ,
,![]() 分别是
分别是![]() 的中点。
的中点。
(1)求![]() 的长;
的长;
(2)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)求证:![]() 。
。
17. (本小题满分12分)
如图,在正四棱柱![]() 中,
中,![]() ,点
,点![]() 为棱
为棱![]() 的中点。
的中点。
(1)证明:![]() //平面
//平面![]() ; (2)求直线
; (2)求直线![]() 到平面
到平面![]() 的距离;
的距离;
 (3)求直线
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值。
所成角的正弦值。
| |||
| |||
18.(本小题满分12分)
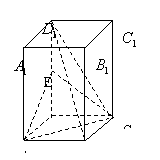
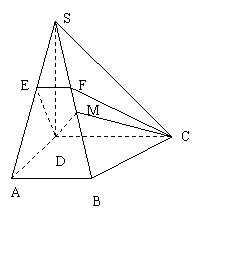
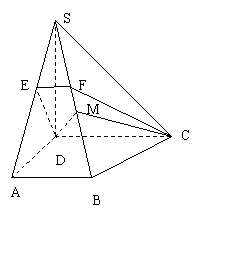
在如图所示的三棱锥![]() 中,
中,![]() 和平面
和平面![]() 所成的角为
所成的角为![]() 。
。
(1)求证:平面![]() ; (2)求三棱锥
; (2)求三棱锥![]() 的全面积
的全面积![]() ;
;
(3)求证:![]() 四点在同一球面上。
四点在同一球面上。
19. (本小题满分14分)
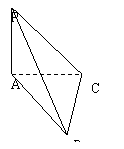
 如图,在直角梯形
如图,在直角梯形![]() 中,
中,![]() 平面
平面![]() ,
,![]() ,在线段
,在线段![]() 上取一点
上取一点![]() (不含端点),
(不含端点),
使![]() ,截面
,截面![]() 与
与![]() 交于点
交于点![]() 。
。
(1)求证:四边形![]() 为直角梯形;
为直角梯形;
(2)求二面角![]() 的平面角的正切值;
的平面角的正切值;
(3)设![]() 的中点为
的中点为![]() ,当
,当![]() 为何值时,
为何值时,
能使![]() ?请给出证明。
?请给出证明。
2005学年第二学期期中杭州地区七校联考答案
高二年级数学学科
一、选择题:(本题每小题3分,共30分)
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| D | B | C | C | D | A | B | D | C | A |
二、填空题:(本题每小题4分,共20分)
11.2
12.49或7
13. ![]()
|
 14.①,③,④
14.①,③,④三、解答题(本大题4小题,共50分)
|
解:(1)以C为原点,
![]() 所在直线为x,y,z轴
所在直线为x,y,z轴
建立空间直角坐标系C-xyz,
则B(0,1,0),N(1,0,1),
![]() ;
; ![]() 4分
4分
|
|
|
|
|
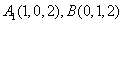
![]()
![]()
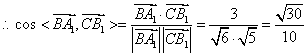
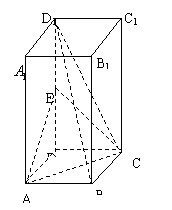 所以,异面直线
所以,异面直线![]() 与
与![]() 所成角的余弦值是
所成角的余弦值是![]() 。
。![]() 4分
4分
(3)![]()
![]()
![]()
![]()
![]() 。
。 ![]() 4分
4分
17.(本小题满分12分)
解:(1)连结BD交AC于 O,连结EO,
可知![]() ,又EO
,又EO![]() 平面
平面![]() ,
,
所以![]() //平面
//平面![]() ;
;
![]() 4分
4分
(2)以D为原点,![]() 所在直线为x,y,z轴建立空间直角坐标系,
所在直线为x,y,z轴建立空间直角坐标系,
则A(2,0,0),C(0,2,0),E(0,0,2),0(1,1,0),设平面![]() 的一个法向量为
的一个法向量为![]() =(x,y,z),又
=(x,y,z),又![]() ,
,![]() ,可得平面
,可得平面![]() 的一个法向量为
的一个法向量为![]() ,又
,又![]() ,所以直线
,所以直线![]() 到平面
到平面![]() 的距离为
的距离为 。
。
![]() 4分
4分
(3)![]() ,
,![]() 面
面![]() ,
,
所以![]() 即为直线
即为直线![]() 与平面
与平面![]() 所成的角。
所成的角。
![]() ,,则sin
,,则sin![]() =
=![]() ,
,
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() 。
。
![]() 4分
4分
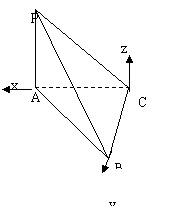 18.(本小题满分12分)
18.(本小题满分12分)
解:(1)由已知![]()
![]() 为等腰直角三角形,且
为等腰直角三角形,且![]() 。
。
在![]() 中,
中,![]() ,
,
![]() ,
,![]() 为等腰直角三角形。
为等腰直角三角形。
![]()
![]()
![]() ,
,
![]()
![]() 平面
平面![]() 。
。 ![]() 4分
4分
法2:以CA,CB所在直线分别为x,y轴建系则A(1,0,0),B(0,![]() ,0),
,0),
C(0,0,0),P(1,0,1)则![]() ,
,
设平面PBC的法向量为![]() ,则
,则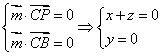 ,取
,取![]() ,
,
又平面PAC的一个法向量为![]() ,
,
![]() ,
,![]() 平面
平面![]() 。
。
![]() 4分
4分
(2)全面积![]()
![]() 。
。
![]() 4分
4分
(3)取PB中点O,由上可知,![]() ,
,![]()
同理,![]() ,
,![]() ,
,![]()
 所以
所以![]() 四点在同一球面上。
四点在同一球面上。
![]() 4分
4分
19.(本小题满分14分)
解:(1)![]() 平面
平面![]() ,
,
![]() 平面
平面![]() 。
。
![]()
![]() 。又
。又![]() 平面ABCD,
平面ABCD,
![]() ,
,![]() 平面SAD,
平面SAD,
![]() ,
,
又![]()
![]() 为直角梯形。
为直角梯形。
![]() 4分
4分
(2)![]() ,
,
![]() 即为二面角
即为二面角![]() 的平面角。
的平面角。![]() 2分
2分
![]() 。
。
![]()
![]() ,
,![]() 2分
2分
![]() ,二面角
,二面角![]() 的平面角的正切值为
的平面角的正切值为![]() 。
。 ![]() 2分
2分
法2:分别以DA,DC,DS所在直线为x,y,z轴建系,则![]() 设
设![]() ,由
,由![]() 在
在![]() 上,可得
上,可得![]() ,又
,又![]() ,
,![]() ,
,
![]()
![]() 2分
2分
设平面BEF的法向量为![]() ,则
,则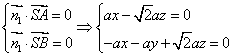
可得![]()
同理可得平面EFCD的法向量为![]()
![]() 2分
2分
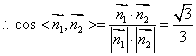
二面角![]() 的平面角的正切值为
的平面角的正切值为![]() 。
。
![]() 2分
2分
(3)当![]() =2时,
=2时,![]() 。
。
![]() ,
,![]()
又![]()
![]()
![]()
![]()
![]() 4分
4分
法2:![]() ,
,
若![]() ,则
,则![]() ,即
,即![]()
得![]() ,所以,当
,所以,当![]() =2时,有
=2时,有![]() 。
。
![]() 4分
4分