不等式章节测试
第Ⅰ卷
一、选择题
1、已知a＞b＞c且a + b + c = 0，下列不等式中恒成立的是( )
A、a2＞b2＞c2 B、a b｜＞c b C、a c＞b c D、a b ＞a c
2、设a = 
，c = 
，若x＞1，则a、b、c的大小关系是( )
A、a＜b＜c B、b＜c＜a C、c＜a＜b D、c＜b＜a
3、如果a2 + b2 = 1，c2 + d2 = 1，则( )
A、abcd＜
B、abcd＞－ C、－＜abcd＜
D、－≤abcd≤
4、已知 a ≠ b｜，m = 
，则m、n之间的大小关系是( )
A、m＞n B、m＜n C、m = n D、m ≤ n
5、不等式
的解集是( )
A、
B、
C、
D、
-
6、不等式组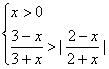
的解集是( )
A、{x 0 ＜x ＜3} B、{x 0 ＜x
C、{ x 0 ＜ x ＜2} D、{ x 0＜ x ＜ 2．5}
7、函数
的( )
A、最小值是－2 B、最大值是－2 C、最小值是2 D、最大值是2
8、在x
范围内恒有 log
，则a的取值范围是( )
A、a≥3 B、0＜a≤
C、a≥3或0＜a≤ D、a＞3或0＜a＜
9、若－3 ＜a＜ 4，则不等式(12 + x－x2)(x－a) ＜0的解集是( )
A、
B、
C、
D、
10、若方程7x2－(k + 13)x + k2－k－2 = 0 有两个实根x1,x2且0＜x1＜1＜x2＜2,则k的取值范围是( )
A、－2＜k＜－1 B、3＜k＜4 C、－2＜k＜4 D、－2＜k＜－1 或3＜k＜4
11、函数f(x)，g(x)定义域为R，且f(x)≥0的解集为{x 1≤x＜2}，g(x)≥0的解集为φ，则不等式f(x)·g(x)＞0的解集为( )
A、{x x＜1或x≥2} B、φ C、R D、{x 1≤x＜2}
12、已知x2 + y2 + z2 = 1，则下列不等式中成立的是( )
A、(x + y + z)2 ≥1 B、xy + yz + zx
C、 xyz ≤
D、x3 + y3 + z3 ≥
二、填空题
13、不等式
的解集是 。
14、若a＞0，b＞0则以下两式的大小关系是：lg
。
15、函数
的值域是 。
16、如果
的取值范围是
。
17、a，b
，当a = ，b = 时，不等式a2
+ b2＞2(a + b－1)不成立。
18、已知关于x的不等式 ax + 2＜8的解集为(－3，5)，则a = 。
19、设n为自然数，a、b为正实数，且满足a + b = 2，则
的最小值是 。
20、设函数
的最大值为4，最小值为－1，则a、b的值为 。
三、解答题
21、设x
R,比较
与1－x的大小。
22、a，b，求证：a2 + b2 +3
。
23、解不等式2log
。
24、解不等式
。
25、设A= {x1＜x＜3}，又设B是关于x的不等式组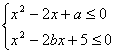
的解集，试求a、b的取值范范围使得A
B。
26、在某两个正数x、y之间，插入一个数a，使x、a、y成等差数列，插入两个数b、c，使x、b、c、y成等比数列，求证：(a + 1 )2 ≥(b + 1) (c + 1)。
27、设
(1)求f(x)的定义域；
(2)f(x)是否存在最大值或最小值？如果存在，请把它求出来。
28、已知f(x) = log ax， f(x) 的图象如图所示，解不等式f(x2－1)＞f(x + a)。
 |
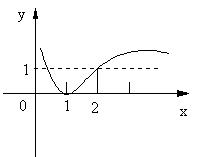29、某种汽车，购买时费用为10万元，每年交保险费、养路费及汽油费合计为9千元，汽车的维护费，第一年为2千元，第二年为4千元，第三年为6千元，依等差数列递增，问使用多少年平均费用最少？
30、设f(x)是定义在[－1，1]上的奇函数,且对任意a，b[－1，1]，当a + b≠时，都有
。
(1)若a＞b，试比较f(a)与f(b)的大小；
(2)解不等式
；
(3)如果g(x) = f(x－c)和h(x) = f(x－c2)这两个函数的定义域的交集是空集，求c的取值范围。
参考答案
一、选择题
1、D 2、C 3、D 4、D 5、A 6、B
7、B 8、C 9、B 10、D 11、A 12、C
二、填空题
13、
14、≤ 15、
16、
17、1，1 18、－2 19、1 20、
三、解答题
21、
22、证明：∵
∴
23、当a = 2时，不等式的解为x
；
当a＞2时，不等式的解为
；
当
。
24、
25、
26、证明：由等差、等比数列的定义，得
由x、y表示a、b、c解得
∴
∴
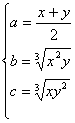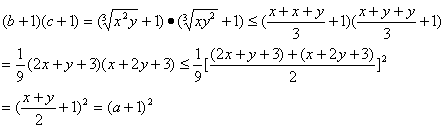
27、(1)(1,p)；
(2)当
无最大值和最小值；
28、
29、10年；最少为3万元。
30、(1)f(a)＞f(b);
(2)
}
(3)