2005杭州二中高二期末考试数学试题（理）
考试时间：120分钟 满分150分
一．选择题：本大题共10小题；每小题5分，共50分．在每小题给出的四个选项中，只有一个选项是符合题目要求的．
1．集合
，则
（A）
（B）
（C）
（D）
2．设地球的半径为
，若在东经
的经线上有北纬
的点A和南纬
的点B，则A、B两点的球面距离是
（A）
（B）
（C）
（D）
3．已知公差不为零的等差数列
的前
项的和为
，若
，
，则
的值是
（A）4 （B）5 （C）7 （D）8
4．已知点
三点共线，那么
的值分别为
（A）
（B）
（C）
（D）
5．在
中，已知
，则：①
；②
；③
；④
；⑤
．其中正确的是
（A）①②④ （B）②③⑤ （C）②④⑤ （D）①③⑤
6．设有如下三个条件：
相交直线
都在平面
内，且都不在平面
内；
直线之中至少有一条与平面相交；
平面与平面相交．当
成立时，
是
的
（A）充分非必要条件 （B）必要不充分条件
（C）充分且必要条件 （D）既不充分也不必要条件
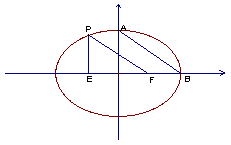
7．椭圆的中心在原点，焦点
在
轴上，A，B是椭圆的顶点，P是椭圆上一点，且
轴，
，则此椭圆的离心率等于
（A）
（B）
（C）
（D）
8．甲、乙两人同时独立地打靶，谁先打中谁胜（如两人在同一次都打中，则为和局，比赛结束），已知甲命中概率为
，乙命中概率为
，则第二轮分出胜负的概率为
（A）
（B）
（C）
（D）
9．设
，则函数
的最大值是
（A）
（B）
（C）
（D）
10．关于的方程
在
有两个不同的实根，则实数
的取值范围是
（A）
（B）
（C）
（D）
二．填空题：本大题共4小题；每小题4分，共16分．请把答案填在题中的横线上．
11．棱长为
的正方体的外接球的表面积是
．
12．已知
，若
，则实数= ．
13．已知某篮球选手罚球投蓝的命中概率为
，在进行三次罚蓝中命中两次的概率为
（用数字做答）．
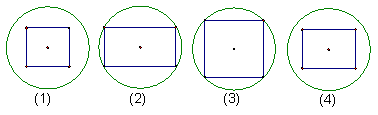
14．已知球内接正方体，则下列图形中可以是过球心的截面的序号是 ．
2005杭州二中高二期末考试数学答题卷
| 题号 | 一 |
| 三
15 16 17 18 19 20 | 总分 |
| 得分 |
|
|
|
|
二
一．选择题：本大题共10小题；每小题5分，共50分．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二．填空题：本大题共4小题；每小题4分，共16分．
11． 12．
13． 14．
三．解答题：本大题共6小题，每小题14分，共84分．解答应写出必要的文字说明、证明过程及演算步骤．
15．（本小题14分）解不等式
．
16．（本小题14分）已知数字1，2，3，4，5，6，7，8，9．
（Ⅰ）能组成多少个数字不重复的四为位偶数？
（Ⅱ）能组成多少个百位数字大于十位数字且十位数字大于个位数字的三位数？
（Ⅲ）如果把9个数字平均分成三组，求三组都成等差数列的概率．
17．（本小题14分）在四棱锥P—ABCD中，
底面ABCD，
，若
．
（Ⅰ）求证：平面PBD
平面PAC；
（Ⅱ）当
时，求点A到平面PDC的距离；
（Ⅲ）当
为何值时，点A在平面PBD的射影恰好是
的重心．
18．（本小题14分）某学校的甲同学参加智力竞赛，乙同学参加演讲比赛，竞赛组委会规定每项竞赛只设金、银两个奖项，已知甲同学获金牌的概率为
，获银牌的概率为
，乙同学获金牌的概率为，获银牌的概率为，为鼓励学生获得好成绩，学校决定：如果学生获金牌则奖励助学金2万元，如果学生获银牌则奖励助学金1万元，不获奖则不发助学金．求学校奖金数
（万元）的概率分布列及数学期望．
19．（本小题14分）已知函数
的最小值为1．
（Ⅰ）若不等式
对任意
恒成立，求实数的取值范围；
（Ⅱ）设数列中，
，且满足：
，用数学归纳法证明：
．
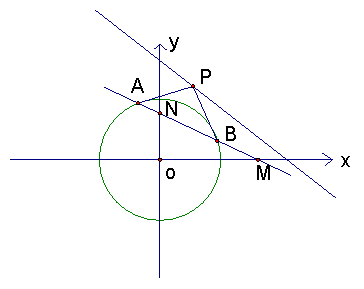
20．（本小题14分）已知点P
是直线
上的一动点，由点P向圆O：
引两条切线，切点分别为A、B，直线AB与轴分别交于点M、N．
（Ⅰ）求
的面积的最小值；
（Ⅱ）是否存在点P，使得
，若存在，求出点P的坐标；若不存在，说明理由．
数学试卷评分细则
一．1~5 C D B A C 6~10 C B A B D
二．11．
；12．
或
；13．
；14．（1）（2）（4）．
三．15．原不等式等价于
， 3分
即
7分
用根轴法得不等式的解为
14分
（注：没有挖去
的扣2分）
16．（Ⅰ）个位数为偶数字
，再从剩下的8个数中选3个进行排列
，
即满足条件的数共有
4分
（Ⅱ）满足题意的三位数等价于从9个数字中任意选择3个进行组合，
即所求的个数为
8分
（Ⅲ）将9个数字平均分成三组的分法总数有
10分
三组都成等差数列的情况有：公差为1的1种
公差为1或2的有2种
公差为1或4的有1种
公差为3的有一种
所以所求的概率为
14分
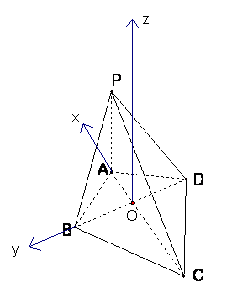
17．解法（一）连接
交于O，以O为原点，CA为轴，DB为
轴，建立如图所示的空间直角坐标系
2分
（Ⅰ）根据题意知
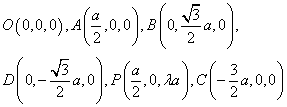
平面PAC的法向量为
，设平面PBD的
法向量为
，则
则
，因为
所以
，故平面PAC平面PBD． 6分
（Ⅱ）设平面PCD的法向量为
，则
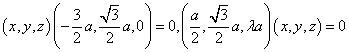
，所以点A到平面PCD的距离为
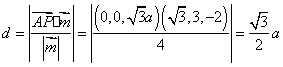10分
（Ⅲ）根据题意得三角形PBD的重心G的坐标为
，由于
平面PBD，所以
14分
解法（二）（Ⅰ）连接交于O，根据题意
，而
平面PAC，因为
平面PBD，因此，平面PAC平面PBD． 3分
（Ⅱ）因为
平面PAD，
∴平面PAD平面PCD
过A向PD作垂线AH，垂足为H，则AH平面PCD，
∴ AH就是点A到平面PDC的距离．
6分
∵
8分
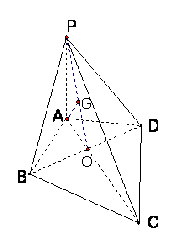（Ⅲ）连接OP，重心G在OP上，且PG=2GO，连接AG，根据题意知，AG平面PBD，
10分
因此，
，
因为
，
∴ 
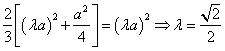
14分
18．解：根据题意的可能取值为4，3，2，1，0
4分
当
，则甲、乙都得金牌，
5分
当
，则甲得金牌且乙得银牌或乙得金牌且甲得银牌，
6分
当
，则甲得金牌乙不得牌或乙得金牌甲不得牌或甲、乙都得银牌
7分
当
，则甲得银牌乙不得牌或乙得银牌甲不得牌，
8分
当
，则甲、乙都不得牌，
9分
随机变量的分布列为
|
| 4 | 3 | 2 | 1 | 0 |
|
|
|
|
|
|
|
11分
因此，
13分
答：学校奖金数的数学期望为
万元．
14分
19．解：因为
2分
（1）
，当时，
所以不等式对任意恒成立，只要
即
5分
（2），即
7分
下面用数学归纳法证明：
①当
时，由已知
9分
②假设
时，命题成立，即
10分
当
时，有
11分
因为，则
，则
．
即命题也成立． 13分
根据①②知，命题对任何自然数
1都成立．
14分
20．（1）设点P的坐标为
，则AB的方程为
3分
所以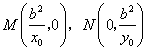
，
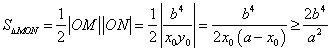
当且仅当
时，取到等号．
6分
（2）假设存在
，满足，连接AO、BO，根据题意知四边形OAPB是正方形，则
，根据几何意义知圆心O到直线的距离是
8分
因此，当
时，不存在满足条件的点P； 9分
当
时，有一个点
满足条件；
11分
当
时，存在两个点
，
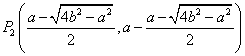满足条件．
14分