高二数学练习（1）
一、选择题（每小题4分，共40分）
1．a,b,c,d∈R，满足条件a+d=b+c，且a-d<b-c，则有（ ）
（A）ad=bc （B）ad>bc
（C）ad<bc （D）ad与bc的大小关系不确定
2．若a,b,c,d∈R，设
；
,则有（ ）
（A）x≤y （B）x≥y
（C）x<y （D）x>y
3．若a>b,c>d，则有（ ）
（A）ac>bd
（B）ad+bc<ac+bd
（C）
（D）
4．下列命题：
①a>b,
②a>b,a,
③a>b,
④
,
⑤
。其中正确的是（ ）
（A）①②③④ （B）①②④⑤
（C）②④⑤ （D）①②⑤
5．已知
，则有（ ）
（A）
（B）
（C）
（D）
6．已知x>0,y>0且x+y≤4，则下列不等式中恒成立的是（ ）
（A）
（B）
（C）
（D）
7．若a,
，a≠b,且a+b=2，则下列不等式成立的是（ ）
（A）
（B）
（C）
（D）以上都不对
8．若已知A（2，3），B（1，5），则直线AB的倾斜角是（ ）
（A）arctg2
（B）arctg(-2)
（C）
（D）
9．过点（1，2）倾斜角α的正切值等于
的直线方程是（ ）
（A）
（B）
（C）
（D）以上都不对
10．一条直线过点P（a,-b）,(ab≠0)且在x轴与y轴上的截距相等，那么满足这样条件的直线（ ）
（A）只有一条
（B）最多有两条
（C）最多有三条
（D）有无数条
二、填空题（每小题5分，共20分）
11．已知a、b、c、d∈R，且有
，
，则abcd的取值范围是 _______。
12．若a,，且a≠b，则
与
的大小关系是_________________，
13．已知同一直线上三点顺次为A(-y,6)，B(-2,y)，C(x,-6)若
，则x=________y=_________.
14．直线
的倾角是
，则m的值为________。
三、解答题（每题10分，共40分）
15．已知a，b，
，且a+b+c=1，求证：
16．已知m>n>0,求证：
17．在直角三角形ABC中，∠A=90°，D，E三等分斜边BC，若AD=sinx，AE=cosx，求斜边BC的长
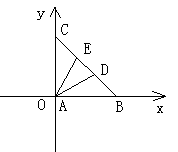
18．已知一条直线过点（-2，3）且在两坐标轴上截距的和是2，求此直线方程
参考答案
一、1B 2A 3B 4 B 5C 6D
7B 8D 9D 10B
二、11．[
]
12．
13．-4，-2
14．3
三、15．证法1：∵a，b，
∴
∴
又∵a+b+c=1，
∴
∴
证法2：欲证原式成立只须证：
即：
∵a+b+c=1
只须证：
∵
∴
∴原不等式成立
16．证：∵m>n>0
∴m-n>0
∴
∴
17.解：如图，建立直角坐标系，设A（0，0）B（b,0）C(0，c)，
∵D、E是
的三等分点。
∴有
，
∴
，
，
这样有
∴
18．解：∵直线在坐标轴上截距和为2
∴截距不能为零
设所求的直线方程为
∵点（-2，3）在直线上
∴
①
又由已知a+b=2②
解①②组成方程组
或 
∴直线方程为
或 