2004－2005学年度上学期
高中学生学科素质训练
高二数学同步测试（3）—不等式的解法
一、选择题（本大题共10小题，每小题5分，共50分）
1．关于
的不等式
的解集不可能是
（ ）
A．
B．
C．
D．
2．下列不等式中，解集为R的是 （ ）
A．x－3>x－3 B．
> 1 C．
D．
3．若
，则
（ ）
A．x<—2或x>3 B．－2<x<3 C．x<－3或x>2 D．－3<x<2
4．a>0，b>0，关于的不等式
的解集为
（ ）
A．
或
B．
或
C．
或
D．
5．不等式
的解集是
（ ）
A．
B．
C．
D．
6．不等式
的解为
（ ）
A．－1<x≤1或x≥2 B．x<－3或1≤x≤2
C．x=4或－3<x≤1或x≥2 D．x=4或x<－3或1≤x≤2
7．设
，
，则集合
满足
（ ）
A．
B．
C．
D．
8．若
，则a的取值范围是
（ ）
A．a>1 B．
C．
D．
或a>1
9．使关于的不等式
能成立的条件是 （ ）
A．0<a<
B．0<a
1 C．<a<1
D．a>1
10．已知函数
、
，且不等式
的解集是
，
不等式
的解集是
，则解集与的关系是 （ ）
A．M 
N
B．
C．
D．N M
二、填空题（本大题共4小题，每小题6分，共24分）
11．不等式2
的解集是
.
12．不等式(x+5)
≥0的解集是
.
13．不等式
≥0的解集是_________________________.
14．若不等式
对一切实数，
都成立，则实数
的取值范围是
.
三、解答题（本大题共6题，共76分）
15．解不等式：
．（12分）
16．解不等式
．（12分）
17．已知函数
在区间
上是增函数，求的取值范围．（12分）
18．求适合不等式
的x的整数解．（12分）
19．已知
,
，
，若
，求实数的取值范围．（14分）
20．奇函数
上是增函数，当
时，是否存在实数m，使
对所有的
均成立？若存在，求出适合条件的所有实数m；若不存在，说明理由．（14分）
参考答案
一、选择题（本大题共10小题，每小题5分，共50分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | D | B | B | C | D | D | C | D | D | C |
二、填空题（本大题共4小题，每小题6分，共24分）
11．
12．
13．
14．
三、解答题（本大题共6题，共76分）
15．（12分）[解析]：
∵原不等式
．
16．（12分）．
[解析]：∵原不等式
．
17．（12分）
[解析]： 设
，∵y关于u递减，要使y关于x在
上是减函数
∴u关于x在是减函数，又
① 又
②
由①②知：
．
18．（12分）
[解析]： ∵原不等式组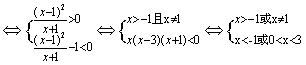
．
19．（14分）
[解析]：由题意可得，A=｛xx－4或x
2｝ B=｛x－2x3｝
则 A
B={x2x3}而C=｛x(x－a)(x－3a)0｝
要使AB
则a>0，
且
，
得 a
．
20．（14分）
[解析]: 易知
，
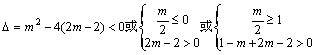
因此，满足条件的实数m存在，它可取
内的一切值．