函数练习综合答案 参考答案与提示
第二章函数
练习1
1.C; 2. A; 3. B; 4. 8; 5. a=3,b= -10,7在f下的象是11; 6. X=A,Y
B
练习2
1． B；2. B; 3. C;
4. [-1,2],[0,
]; 5. 5; 6.（1）x>0或x<-1 （2）（－
，－1）
（-1，0）7. 宽为
米，长为4米时，总面积最大为
练习3
1．C ; 2. D ; 3. (1) [4,16) ; (2) [-3,3], (3) (-,0) [0,+ ); 4. -5
; 5. 图象略 ；6.
(-1,0) (0,1) ; 7. 提示：用-x代替x，得2f(-x)+f(x)=-3x+1,与已知等式联立求解，得f(x)=3x+
练习4
1．D ；2. B ；3. (-,0) ，(0,+ ) ；4. p
-1 ；5. 略；6.
m=-8，f(1)=13；7. 提示：先画出y=x2-2x-3的大致图象，再把图象在x轴下方的部分沿x轴翻折上去，由图象得单调递增区间为[-1,1]，[3, + )；8. 图略，在(-,-3]上单调递减，在[3,+ )上单调递增，在[-3,3]上为常函数；9. f(2) 7；
练习5
1.
C ； 2. C ；
3. 1 ；
4. 5，
；5. a=2 ，b=-2； 6. (1) y=
(x
6) , (2) y=1-
(x2) , (3) y=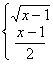
；7. 由已知等式可得x2=
，
x20，
0，y<2 或y3 ；
练习6
1．D ；2. A ；3. 0 ；4. 
(0<x<1)；5. f -1(x)=
，通过比较可知m= -2；6.
a=2，b=0；7. f(x)= 
，f -1(x)= 
，f -1(
)=
；
练习7
1．B ；2. A ；3. a ；4. -2 ；5.
[0,2)(2,+)；6. a=
，b=1，令x=3，则f(3)=1，(3,1)在f(x)的图象上，则(1,3)在g(x)的图象上，c=6；7. a
；8. f -1(x)=
；
练习8
1．D；2. D；3. -3；4. 
；5. (1) 
；(2) 
；6. (1) 
；(2) 
；7. 18；
练习9
1. A；2. B ；3. D ；4. D ；5. C ；6. D ；7. 
；8. 
；9. 2； 10.
(1) 
；(2) 
；(3) 0 ；11. ；
练习10
1．D ；2. D ；3. 512 ；4. (1) a>1 , (2) a>1 , (3) 0<a<1 ；5. (1) R , (0,1] , (2) (-,0] , [0,1) ； 6. a<-2或a>1；7. 设2x=t，则y=t2-()t+1，t
(0,+ )，又t2-()t+1=(t-1)2+
，当t=
时达到最小值，故函数当x=-2时，达到最小值。
练习11
1．B；2. A ；3. (1) x轴；(2) y轴；(3)
原点；4. 左，1，下，3；5. x
时单调递减，x>时，单调递增；6. m-5；7. (1)图略；(2)
(-,2]上单调递减，(2，+)上单调递增；
练习12
1．A；2. B ；3. >0，=0，<0；4. (-2，-2) ；5. (1)
<，(2) >，(3) >；6. 0<y<1；7. 
练习13
1．B；2.
D ；3．（1）
625=4；（2）
=-6；（3）
27=a；（4）
；4. (1)
＝9(2)
＝125 (3)
＝ (4) 
＝
； 5. ；6．(1) 25＝
＝2 (2) 
＝－4 (3) 
100＝2 (4) 0.01＝－2；7.
1125 ；
练习14
1．
C；2. B ；3. (1) 1，(2) 0，(3) 5，(4) 2；4. -2 ；5. x=8 ；6. 0 ；7. (1)
2000；(2) 48；8. (-7，-6)(-6，-5) (-1，+)
练习15
1． D；2. D；3. ab=1；4.(1)
19；(2)
；5. (1) 0；(2)
；(3) ；6. 1；7. 2 ；
练习16
1．B ；2. D ；3. y=10x+1 xR；4.｛xx<-4或x>1｝；5. f -1(x)=log5(x+1)，x>-1；6. P={x1<x<2}，Q={xx<4},P
Q={xx<2}；7. （
，1000），
练习17
1．A；2. A ；3. B；4. (1,2)(2,3)；5. (-，-2］；6. 
；7. (1) 当
时，定义域为
；当
时，定义域为
；(2) 当时解得
当时解得
；
练习18
1．解：∵底面边长为a-2x,∴底面积为(a-2x)
又长方体高为x,∴长方体体积V=x(a-2x)
由a-2x＞0,得x＜
又x＞0,∴函数定义域为{x0＜x＜
.
2.
解：设底面的另一边长为z(m)，则根据题意有6xz=8000,z=
池壁造价为a·(2x+2z)·6=12a(x+)池底造价为2a·
a所以，总造价：y=［12a(x+)+
a］(元)
3. 解：作AC⊥CE，BD⊥CE，∴Rt△BDE面积：h，矩形面积：2h∴A=S矩+2
=2h+2×h=h+2h(m)
4. 解：设商品售价定为x元时，利润为y元，则y=(x-8)[60-10(x-10)]=-10[(x-12)-16]=-10(x-12)+160
(x>10)当且仅当x=12时，y有最大值160元，即售价定为12元时可获最大利润160元。
第二章 综合检测
1.D 2.D
3.C 4.D 5.B
6.A 7.A 8.A
9.B 10.C 11. C 12.D 13．
14.2个 15．
16、184.50元
17.
18.(1)a＞1时，
；0＜ａ＜1时，
19.