江苏省上冈高级中学数学二轮复习材料

数学思想—数形结合　主备：韩洪廷

一．选择题：

1.使sinx≤cosx成立的x的一个变化区间是　　　　( 　 )

A.  　　　　 B.  　　　C. 　　　D.

2.0<a<1,函数y=a^x与y=(a-1) x²的图像只可能是　　　　　　　　 (　　)

 

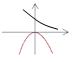
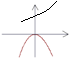
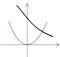
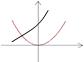
A.　　　　　　　B.　 　　　　　C. 　　　　　　　D.

3.已知线段AB的两个端点的坐标为A(2,-3),B(-3,-2)，直线l过点P(1,1)与线段AB相交，则直线l的斜率k的取值范围是 （　　）　　　　　　　　　　　　　　　　　 　　　　　 

A. ≤k≤　　 B. k≤-4或k≥ 　　　C. k≠　　　　 D. k∈R

4.集合M={(x,y) x²+y²=9 (0< y <1)},集合N={(x,y) y= x+b},若M∩N≠Φ,则实数b满足(　  )

A.≤b≤ 　　 B.-3≤b ≤　　　 C.0<b≤ 　　　D. -3<b ≤

5.已知x, y之间的关系式x²+y²-6x-6y+17=0，则 (　 )

 A.既有最大值，又有最小值　　  　　　B. 既无最大值，又无最小值　　　　

C. 有最大值，而无最小值　　　　  　　D. 无最大值，有最小值

6．设α是第二象限的角，则有　　　 (　 )

A.　　 B.　　  C.　　　 D.

二．填空题：

7．方程x²-2 x-p=0有两个不相等的实数根，则常数p的值为__________________________

8．已知方程ax²+bx+a=0 (ab>0)的解集为Φ，则a²+b²-2b的取值范围是___________________

9．函数的最小值为_______________

10. 已知x, y∈R且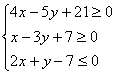，则z=x+2y的最大值为________________

三．解答题：

11. 已知f(x)=(x+1)x-1,方程f(x)= x +m有三个不同的实数解,求实数m的取值范围

12.设f(x)是x在[-1,1]上的偶函数，f(x)与g(x)的图象关于x=1对称，且当x∈[2,3]时，g(x)=2a(x-2)-4(x-2)³ (a为常数)

 ①求函数f(x)的表达式：

 ②设a∈(2,6)或a∈(6,+∞)，分别求a的值，使f(x)的最大值为12.

13.P是双曲线上任意一点，过P作与双曲线渐近线平行的直线分别与这两条直线交于Q,R，求证：平行四边形OQPR的面积是与P的位置无关的常数，并求此常数