高三数学二轮复习授纲•立几（2）（孙环海）
1．a,b表平面，m, n表示直线，则m‖a的一个充分条件是 （ ）
A.a⊥b且m⊥b
B.a∩b=n 且m‖n
C.m‖n且n‖a D. a‖b 且mÌb
2．在直二面角a-L-b中，直线aÌa，直线bÌb，a ,b与L斜交，则 （ ）
A. a不和b垂直，但可能a‖b B.a可能与b垂直，也可能a‖b
C. a与b不垂直也不平行 D.a不和b平行，但可能a⊥b
3．设a,b,c是两两异面的三条直线，已知a⊥b且d是a,b的公垂线，如果c⊥a，那么c与 d的位置关系为 ( )
A.相交 B.平行 C.异面 D.异面或平行
4．如果a,b是异面直线，P是不在a,b上的任意一点，下列四个结论：
①过P一定可作直线L与a,b都相交。②过P一定可作直线L与a,b都垂直。③过P一定可作平面a与a,b都平行。④过P一定可作直线L与a,b都平行。其中正确的结论有
A.0个 B.1个 C.2个 D.3个
5．教室内的一把直尺无论如何放置，在地面上总有直线与它 （ ）
A.平行 B.相交 C.异面 D.垂直
6．空间两条异面直线a,b所成角为600，过空间一定点O与a,b所成角都为450的直线有
_______________________条。
7．棱长为1的正四面体，P,Q是一组对棱上的两点，则Q, P的最短距离为__________________
8．异面直线a,b成600，直线c⊥a，则直线b与c所成角q的范围是_____________________
9．已知面a有ÐBAC=600，点P在a外，PA=2，P到AB,AC的距离均为
，则PA与面a所成角的余弦值为________________________
10．在二面角a-L-b的一个平面a内有一条直线AB，它与棱L所成角为450，与平面b所成角的为300，则这个二面角的大小为___________________________
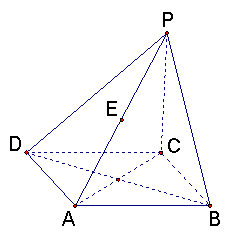
11．已知：如图，边长为a的菱形ABCD中，ÐABC=60°，PC⊥面ABCD，E是PA的中点，求E到平面PBC的距离。
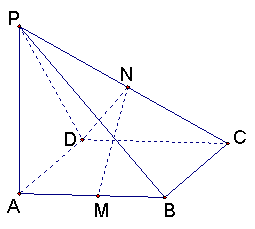
12．如图所示，PA⊥面ABCD，四边形ABCD是矩形，PA=AD=a,M,N分别是AB,CP中点。
（1）求面PCD与面ABCD所成二面角大小。
（2）求证：面MND⊥面PCD.
（3）当AB长度变化时，求异面直线PC与AD所成角的可能范围。
13．如图：在正三棱柱ABC-A1B1C1中，AB=3,AA1=4,M为AA1中点，P是BC上一点，且由P沿棱柱侧面经过棱CC1到M的最短路线长为
，设这条最短路线与CC1的交点为N：
（1）求该三棱柱的侧面展开图的对角线的长
（2）PC和NC的长
（3）平面MNP与平面ABC所成二面角（锐角）的大小。
