第九章单元综合训练(二)
班级 姓名 学号
一、选择题
1.下列棱柱是正四棱柱的是 ( )
(A)底面是正方形,有两个侧面是矩形.
(B)底面是正方形,有两个侧面垂直于底面.
(C)底面是矩形,两个相邻侧面分别是矩形和正方形.
(D)四个侧面是全等的矩形.
2.过球面上任意两点,可以作的大圆的个数为 ( )
(A)1个 (B)2个
(C)无数多个 (D)无数多个或1个
3.正六棱柱ABCDEF-A1B1C1D1E1F1的底面边长为1,侧棱长为,则这个棱柱的侧面对角线E1D与BC1所成的角为 ( )
(A)90° (B)60° (C)45° (D)30°
4.一个圆柱的侧面展开图是一个正方形,这个圆柱的全面积与侧面积的比是 ( )
(A) (B) (C) (D)
5.在斜棱柱的侧面中矩形最多有 ( )
(A)2个 (B)3个 (C)4个 (D)6个
6.一个表面积为p的球内挖去一个最大的正方体,则所剩下的几何体的体积是( )
(A)- (B)- (C)- (D)-
7.在四棱锥A-BCDE中,AB⊥底面BCDE,且BCDE为正方形,则四棱中互相垂直的面有 ( )
(A)6对 (B)5对 (C)4对 (D)3对
8.一个长方体的表面积为22cm2,体积是8cm3,这样的长方体 ( )
(A)只有一个 (B)只有两个 (C)无数多个 (D)不存在
9.设命题甲“直四棱柱ABCD-A1B1C1D1中,平面ACB1与对角面BB1D1D垂直”;命题乙:“直四棱柱ABCD-A1B1C1D1是正方体”,那么甲是乙的 ( )
(A)充分必要条件 (B)充分非必要条件
(C)必要非充分条件 (D)既非充分也非必要条件
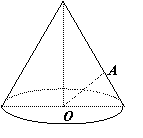 10.如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得的曲面将圆锥分成体积相等的两部分,则母线与轴的夹角的余弦值为 ( )
10.如图,OA是圆锥底面中心O到母线的垂线,OA绕轴旋转一周所得的曲面将圆锥分成体积相等的两部分,则母线与轴的夹角的余弦值为 ( )
(A) (B) (C) (D)
二、填空题
1.若一个圆柱的底面直径和高都等于一个球的直径,则这个圆柱的体积和球的体积之比为 .
2.正六面体每个面的中心是一个正八面体的顶点,则这个正六面体和正八面体的体积之比为 .
3.在长方体ABCD-A1B1C1D1中,对角线AC1与AA1、AD均成60°角,那么它与AB所成的角为 .
4.一个简单多面体,各个面的内角和为3600°,则它的面数为 .
三、解答题
1.已知三棱锥A-BCD的各棱长均为a,点P在棱AB上,点Q在棱CD上,求点P和点Q的距离最小值.
2.设地球是半径为R的球,地球上A、B两地都在北纬45°上,A、B两点的球面距离是pR,A在东经20°,求点B的位置.
3.如图,在多面体ABCD-A1B1C1D1中,上、下底面平行且均为矩形,相对的侧面与同一底面所成的二面角大小相等,侧棱延长后相交于E、F两点,上、下底面矩形的长、宽分别为c、d与a、b且a>c,b>d两底面间的距离为h.
(1)求侧面ABB1A1与底面ABCD所成的二面角的大小.
(2)证明:EF∥面ABCD.
(3)在估测该多面体的体积时,经常运用近似公式V估=S中截面·h来计算,已知它的体积公式是V=(S上底面+4S中截面+S下底面),试判断V估与V的大小关系,并加以证明.