2008届高三文科数学第二轮复习资料
——《解析几何》专题
1.已知动圆过定点![]() ,且与直线
,且与直线![]() 相切.
相切.
(1) 求动圆的圆心轨迹![]() 的方程;
的方程;
(2) 是否存在直线![]() ,使
,使![]() 过点(0,1),并与轨迹
过点(0,1),并与轨迹![]() 交于
交于![]() 两点,且满足
两点,且满足![]() ?若存在,求出直线
?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
2.如图,设![]() 、
、![]() 分别为椭圆
分别为椭圆![]() :
:![]() (
(![]() )的左、右焦点.
)的左、右焦点.
(Ⅰ)设椭圆C上的点![]() 到F1、F2两点距离之和等于4,写出椭圆C的方程和离心率;
到F1、F2两点距离之和等于4,写出椭圆C的方程和离心率;
(Ⅱ)设点K是(Ⅰ)中所得椭圆上的动点,求线段![]() 的中点的轨迹方程.
的中点的轨迹方程.
3.已知圆C: x2+y2-2x+4y-4=0,是否存在斜率为1的
直线L,使以L 被圆C截得弦AB为直径的圆
经过原点?若存在,写出直线的方程;若不存在,说
明理由![]()
4.已知圆![]() :
:![]() .
.
(1)直线![]() 过点
过点![]() ,且与圆
,且与圆![]() 交于
交于![]() 、
、![]() 两点,若
两点,若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)过圆![]() 上一动点
上一动点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() ,设
,设![]() 与
与![]() 轴的交点为
轴的交点为![]() ,若向量
,若向量![]() ,求动点
,求动点![]() 的轨迹方程,并说明此轨迹是什么曲线.
的轨迹方程,并说明此轨迹是什么曲线.
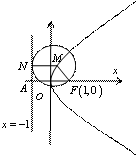
 5.如图,已知圆A的半径是2,圆外一定点N与圆A上的点的最短距离为6,过动点P作A的切线PM(M为切点),连结PN使得PM:PN=
5.如图,已知圆A的半径是2,圆外一定点N与圆A上的点的最短距离为6,过动点P作A的切线PM(M为切点),连结PN使得PM:PN=![]() ,试建立适当
,试建立适当
的坐标系,求动点P的轨迹![]()
6.已知三点P(5,2)、![]() (-6,0)、
(-6,0)、![]() (6,0).
(6,0).
(Ⅰ)求以![]() 、
、![]() 为焦点且过点P的椭圆的标准方程;
为焦点且过点P的椭圆的标准方程;
(Ⅱ)设点P、![]() 、
、![]() 关于直线y=x的对称点分别为
关于直线y=x的对称点分别为![]() 、
、![]() 、
、![]() ,求以
,求以![]() 、
、![]() 为焦点且过点
为焦点且过点![]() 的双曲线的标准方程.
的双曲线的标准方程.
7.某运输公司接受了向抗洪抢险地区每天至少运送180吨支援物资的任务,该公司有8辆载重为6吨的![]() 型卡车与4辆载重为10吨的
型卡车与4辆载重为10吨的![]() 型卡车,有10名驾驶员,每辆卡车每天往返次数为
型卡车,有10名驾驶员,每辆卡车每天往返次数为![]() 型卡车4次,
型卡车4次,![]() 型卡车3次,每辆卡车每天往返的成本费用为
型卡车3次,每辆卡车每天往返的成本费用为![]() 型卡车320元,
型卡车320元,![]() 型卡车504元,请你给该公司调配车辆,使公司所花的成本费用最低.
型卡车504元,请你给该公司调配车辆,使公司所花的成本费用最低.
8.曲线![]() 上两点P、Q满足:①关于直线
上两点P、Q满足:①关于直线![]() 对称;②
对称;②![]() .求直线PQ的方程.
.求直线PQ的方程.
9.两类药片有效成分如下表
|
药品 | 阿斯匹林 ( | 小苏打 ( | 可待因 ( | 每片价格 (元) |
| A(1片) | 2 | 5 | 1 | 0.1 |
| B(1片) | 1 | 7 | 6 | 0.2 |
若要求提供12![]() 阿斯匹林,70
阿斯匹林,70![]() 小苏打,28
小苏打,28![]() 可待因,两类药片的最小总数是多少?在最小总数情况下的两类药片怎样搭配价格最低?
可待因,两类药片的最小总数是多少?在最小总数情况下的两类药片怎样搭配价格最低?
参考答案
 1.解:(1)如图,设
1.解:(1)如图,设![]() 为动圆圆心,
为动圆圆心, ![]()
![]() ,过点
,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,由题意知:
,由题意知:![]() ,
,
即动点![]() 到定点
到定点![]() 与定直线
与定直线![]() 的距离相等,由
的距离相等,由
抛物线的定义知,点![]() 的轨迹为抛物线,其中
的轨迹为抛物线,其中![]()
为焦点,![]() 为准线,
为准线,
∴ 动点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(2)由题可设直线![]() 的方程为
的方程为![]() ,
,
由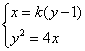 得
得![]()
△![]() ,
,![]() .
.
设![]() ,
,![]() ,则
,则![]() ,
,![]() .
.
由![]() ,即
,即 ![]() ,
,![]() ,于是
,于是![]() ,
,
即![]() ,
,![]() ,
,
![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
又![]() , ∴ 直线
, ∴ 直线![]() 存在,其方程为
存在,其方程为![]()
2.解:(Ⅰ)![]() ,
,
![]() .
.
![]() ,
,![]() .
.
椭圆的方程为![]() ,
,
因为![]() .
.
所以离心率![]() .
.
(Ⅱ)设![]() 的中点为
的中点为![]() ,则点
,则点![]() .
.
又点K在椭圆上,则![]() 中点的轨迹方程为
中点的轨迹方程为![]() .
.
3.解:设直线L的斜率为1,且L的方程为y=x+b,则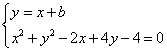 消元得方程
消元得方程
2x2+(2b+2)x+b2+4b-4=0,设此方程两根为x1,x2,则x1+x2=-(b+1),y1+y2= x1+x2+2b=b-1,
则AB中点为![]() ,又弦长为
,又弦长为![]() =
=![]() ,由题意可列式
,由题意可列式![]() =
= 解得b=1或b=-9,经检验b=-9不合题意.所以所求直线方程为y=x+1.
解得b=1或b=-9,经检验b=-9不合题意.所以所求直线方程为y=x+1.
4.解(Ⅰ)①当直线![]() 垂直于
垂直于![]() 轴时,则此时直线方程为
轴时,则此时直线方程为![]() ,
,![]() 与圆的两个交点坐标为
与圆的两个交点坐标为![]() 和
和![]() ,其距离为
,其距离为![]() ,满足题意
,满足题意
②若直线![]() 不垂直于
不垂直于![]() 轴,设其方程为
轴,设其方程为![]() ,即
,即![]()
设圆心到此直线的距离为![]() ,则
,则![]() ,得
,得![]()
∴![]() ,
,![]() ,
,
故所求直线方程为![]()
综上所述,所求直线为![]() 或
或![]()
(Ⅱ)设点![]() 的坐标为
的坐标为![]() ,
,![]() 点坐标为
点坐标为![]()
则![]() 点坐标是
点坐标是![]()
∵![]() ,
,
∴![]() 即
即![]() ,
,![]()
![]()
又∵![]() ,∴
,∴![]()
由已知,直线m //ox轴,所以,![]() ,
,
∴![]() 点的轨迹方程是
点的轨迹方程是![]() ,
,
轨迹是焦点坐标为![]() ,长轴为8的椭圆,并去掉
,长轴为8的椭圆,并去掉![]() 两点.
两点.
5.解:以AN所在直线为x轴,AN的中垂
 线为y轴建立平面直角坐标系如图所示,
线为y轴建立平面直角坐标系如图所示,
则A(-4,0),N(4,0),设P(x,y)
由PM:PN=![]() ,PM2=PA2 –MA2得:
,PM2=PA2 –MA2得:
![]()
代入坐标得:![]()
整理得:![]()
即![]()
所以动点P的轨迹是以点![]()
![]() .
.
6.解:(I)由题意,可设所求椭圆的标准方程为![]() +
+![]()
![]() ,其半焦距
,其半焦距![]() .
.
![]()
![]() , ∴
, ∴![]()
![]() ,
,
![]() ,故所求椭圆的标准方程为
,故所求椭圆的标准方程为![]() +
+![]() ;
;
(II)点P(5,2)、![]() (-6,0)、
(-6,0)、![]() (6,0)关于直线y=x的对称点分别为:
(6,0)关于直线y=x的对称点分别为:
![]() 、
、![]() (0,-6)、
(0,-6)、![]() (0,6)
(0,6)
设所求双曲线的标准方程为![]() -
-![]()
![]() ,由题意知半焦距
,由题意知半焦距![]() ,
,
![]()
![]() , ∴
, ∴![]()
![]() ,
,
![]() ,故所求双曲线的标准方程为
,故所求双曲线的标准方程为![]() -
-![]() .
.
点评:本题主要考查椭圆与双曲线的基本概念、标准方程、几何性质等基础知识和基本运算能力
7.解:该公司调8辆A型车,成本最低.
8.解:![]()
![]()
![]()
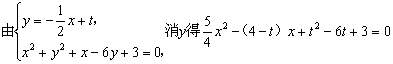 .
.
![]()
![]() .
.
![]()
![]()
![]()
化简得![]()
![]() .
.
 9.解:设A类药x片,B类药y片,
9.解:设A类药x片,B类药y片,
由题意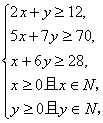
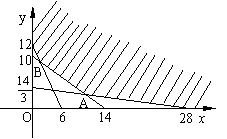
![]() 满足的可行域如图
满足的可行域如图
两类药片的最小总数![]()
由图象可知,最小总数应在B点附近可行域内的整点处取得.
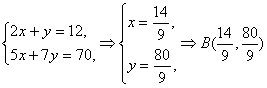
在B点附近可行域内的整点有C(1,10),D(2,9),E(3,8),F(4,8).
![]() 两类药片的最小总数是11片.
两类药片的最小总数是11片.
设在最小总数情况下的两类药片总价格![]() ,
,![]()
![]() ,
,![]() ,
,
即用A类3片B类8片可使价格最低.