2008届高三文科数学第二轮复习资料
——《数列》专题
1.等差数列
的前
项和记为
，已知
.
（1）求通项
；
（2）若
，求；
（3）若
，求数列
的前项和
的最小值.
2.等差数列中，为前项和，已知
.
（1）求数列的通项公式；
（2）若
，求数列的前项和.
3.已知数列满足
，
，记
.
（1）求证:数列为等差数列；
（2）求数列的通项公式.
4.在数列
中，
，
，且当
时，
.
（1）求证数列
为等差数列；
（2）求数列的通项；
（3）当时，设
，求证：
.
5.等差数列中，
.
（1）求数列的通项公式；
（2）设
，求；
（3）设
，
，是否存在最大的整数
使得对任意
，均有
成立，若存在，求出的值，若不存在，请说明理由.
6.已知数列
为等差数列，且
.
（1）求的通项公式；
（2）证明：
.
7.数列
满足
.
（1）求数列的通项公式；
（2）设
，则为何值时，
的项取得最小值，最小值为多少？
8.已知等差数列
的公差
大于
,且
是方程
的两根,数列
的前项和为
,且
.
（1）求数列,的通项公式；
（2）记
，求证:对一切
,有
.
9.数列的前项和
满足
.
（1）求数列的通项公式；
（2）数列中是否存在三项，它们可以构成等差数列？若存在，请求出一组适合条件的项；若不存在，请说明理由.
10. 已知数列的前项和为，设是与2的等差中项，数列中，
，点
在直线
上.
（1）求数列,的通项公式
（2）若数列的前项和为
，比较
与2的大小；
（3）令
，是否存在正整数
，使得
对一切正整数都成立？若存在，求出的最小值；若不存在，请说明理由.
11. 设数列.满足：
，且数列
是等差数列，{bn－2}是等比数列．
（Ⅰ）求数列,的通项公式；
（Ⅱ）是否存在
，使
．若存在，求出k；若不存在，说明理由.
12. 将等差数列的项按如下次序和规则分组，第一组为
，第二组为
，第三组为
，第四组
，第组共有
项组成，并把第组的各项之和记作
，已知
，
（1）求数列的通项公式；
（2）若以
为项构成数列
，试求的前8项之和
（写出具体数值）.
13. 已知数列的前项和满足：
,
.
⑴写出求数列的前3项
；
⑵求数列的通项公式；
⑶证明：对任意的整数m>4，有
.
参考答案
1．
；
；的最小值为：-20．
2.
； 
．
3.
．
4.
．
5.
； 
．
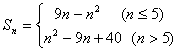6.
．
7. 
；
时，最小为
．
8.
，
．
9.
；不存在．
10.
；
；存在
．
11.
；
；不存在．
12.
； 59415．
13. （1）
；
（2）
（3）由已知得：
.
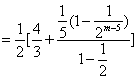
故( m>4).