2009届高三数学复习
必修一《集合与函数》检测题
一、填空题
1.设集合![]() ,定义P※Q=
,定义P※Q=![]() ,则P※Q中元素的个数为
个;12
,则P※Q中元素的个数为
个;12
2.设![]() 、
、![]() 是两个集合,定义
是两个集合,定义![]() ,
,
![]() ,则
,则![]() ;
;![]()
3.一等腰三角形的周长是20,底边y是关于腰长x的函数,它的解析式为
;![]()
4.若![]() 关于 对称;y轴
关于 对称;y轴
5.已知函数f(x)=![]()
![]() 则
则![]() =_________;2
=_________;2
6.若函数![]() 在(1,+∞)上是增函数,则实数p的取值范围是 ;
在(1,+∞)上是增函数,则实数p的取值范围是 ;![]()
7.若关于x的方程![]() 有负实数解,则实数a的取值范围为______;
有负实数解,则实数a的取值范围为______;![]()
8.函数![]() 是幂函数,且在
是幂函数,且在![]() 上是减函数,则实数
上是减函数,则实数![]() ______;2
______;2
9.一个退休职工每年获得一份退休金,金额与他服务的年数的平方根成正比,如果多服务a年,他的退休金会比原来的多p元,如果他多服务b年(b≠a),他的退休金会比原来的多q元,那么他每年的退休金是(用a,b,p,q表示) ;
![]()
10.设f(x)是R上的函数,且f(-x)=-f(x),当x∈[0,+∞)时,f(x)=x(1+![]() ),那么当
),那么当
x∈(-∞,0)时,f(x)=_____ ___;![]()
11.已知函数![]() 是定义在
是定义在![]() 上的奇函数,当
上的奇函数,当![]() 时,
时,

![]() 的图象如图所示,则不等式
的图象如图所示,则不等式![]() 的解集
的解集
是
![]()
12.若对于任意![]() , 函数
, 函数![]() 的值恒大于零, 则
的值恒大于零, 则![]() 的取值范围是
. (-∞‚1)∪(3,+∞)
的取值范围是
. (-∞‚1)∪(3,+∞)
13.国家规定个人稿费纳税办法是:不超过800元的不纳税;超过800 元而不超过4000元的按超过800元部分的14%纳税;超过4000元的按全部稿酬的11%纳税.已知某人出版一本书,共纳税420元时,这个人应得稿费(扣税前)为 元.3800
14.已知函数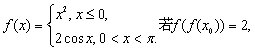 则
则![]() .
. ![]()
二、解答题
15.二次函数![]() 满足
满足![]() 且
且![]() .
.
(Ⅰ)求![]() 的解析式;
的解析式;
(Ⅱ)在区间![]() 上,
上,![]() 的图象恒在
的图象恒在![]() 的图象上方,试确定实数
的图象上方,试确定实数![]() 的范围.
的范围.
解:(Ⅰ)设![]() ,由
,由![]() 得
得![]() ,故
,故![]() .
.
∵![]() ,∴
,∴![]() .
.
即![]() ,所以
,所以![]() ,∴
,∴![]() .
.
(Ⅱ)由题意得![]() 在[-1,1]上恒成立.即
在[-1,1]上恒成立.即![]() 在[-1,1]上恒成立.
在[-1,1]上恒成立.
设![]() ,其图象的对称轴为直线
,其图象的对称轴为直线![]() ,所以
,所以![]() 在[-1,1]上递减.
在[-1,1]上递减.
故只需![]() ,即
,即![]() ,解得
,解得![]() .
.
16.已知集合![]() ,
,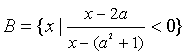 .
.
(Ⅰ)当![]() 时,求
时,求![]() ;
;
(Ⅱ)求使![]() 的实数
的实数![]() 的取值范围.
的取值范围.
解:(1)当![]() 时,
时,![]() ,
,![]() ∴
∴ ![]() .
.
(Ⅱ)∵ ![]() ,
,
当![]() 时,
时,![]()
要使![]()
![]() A,必须
A,必须![]() ,此时
,此时![]() ;
;
当![]() 时,A=
时,A=![]() ,使
,使![]() 的
的![]() 不存在;
不存在;
当![]() 时,A=(2,3
时,A=(2,3![]() +1)
+1)
要使![]()
![]() A,必须
A,必须![]() ,此时1≤
,此时1≤![]() ≤3.
≤3.
综上可知,使![]()
![]() A的实数
A的实数![]() 的取值范围为[1,3]∪{-1}
的取值范围为[1,3]∪{-1}
17.设函数![]() (
(![]() 为实数).
为实数).
(Ⅰ)若![]() ,用函数单调性定义证明:
,用函数单调性定义证明:![]() 在
在![]() 上是增函数;
上是增函数;
(Ⅱ)若![]() ,
,![]() 的图象与
的图象与![]() 的图象关于直线
的图象关于直线![]() 对称,求函数
对称,求函数![]() 的解析式.
的解析式.
解:(Ⅰ)设任意实数![]() ,则
,则![]()
=![]() =
=![]()
![]()
![]() .
.
又![]() ,∴
,∴![]() ,所以
,所以![]() 是增函数.
是增函数.
(Ⅱ)当![]() 时,
时,![]() ,∴
,∴![]() , ∴
, ∴![]() ,
,
y=g(x)= log2(x+1).
18.(本小题满分12分)函数![]() 的定义域为
的定义域为![]() (
(![]() 为实数).
为实数).
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的值域;
的值域;
(Ⅱ)若函数![]() 在定义域上是减函数,求
在定义域上是减函数,求![]() 的取值范围;
的取值范围;
(Ⅲ)求函数![]() 在
在![]()
![]() 上的最大值及最小值,并求出函数取最值时
上的最大值及最小值,并求出函数取最值时![]() 的值.
的值.
解:(Ⅰ)显然函数![]() 的值域为
的值域为![]() ;
;
(Ⅱ)若函数![]() 在定义域上是减函数,则任取
在定义域上是减函数,则任取![]()
![]() 且
且![]() 都有
都有![]() 成立,
成立,
即![]() ,只要
,只要![]() 即可,
即可,
由![]()
![]() ,故
,故![]() ,所以
,所以![]() ,
,
故![]() 的取值范围是
的取值范围是![]() ;
;
解法二:∵![]() 而
而![]() ∴
∴![]() ≤
≤![]()
(3)当![]() 时,函数
时,函数![]() 在
在![]() 上单调增,无最小值,
上单调增,无最小值,
当![]() 时取得最大值
时取得最大值![]() ;
;
由(2)得当![]() 时,函数
时,函数![]() 在
在![]() 上单调减,无最大值,
上单调减,无最大值,
当![]() 时取得最小值
时取得最小值![]() ;
;
当![]() 时,函数
时,函数![]() 在
在![]() 上单调减,在
上单调减,在![]() 上单调增,无最大值,
上单调增,无最大值,
当![]() 时取得最小值
时取得最小值![]() .
.
19.已知:函数![]() (
(![]() 是常数)是奇函数,且满足
是常数)是奇函数,且满足![]() ,
,
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)试判断函数![]() 在区间
在区间![]() 上的单调性并说明理由;
上的单调性并说明理由;
(Ⅲ)试求函数![]() 在区间
在区间![]() 上的最小值.
上的最小值.![]()
解:(Ⅰ)∵函数![]() 是奇函数,则
是奇函数,则![]()
即 ![]() ∴
∴![]()
由![]() 得
得![]()
解得![]() ∴
∴![]() ,
,![]() .
.
(Ⅱ)解法1:由(Ⅰ)知![]() ,
,
∴![]() ,
,
当![]() 时
时![]() ,
,![]()
∴![]() ,即函数
,即函数![]() 在区间
在区间![]() 上为减函数.
上为减函数.
[解法2:设![]() ,
,
则![]() =
=![]()
=![]()
∵![]() ∴
∴![]() ,
,![]() ,
,![]()
∴![]() ,即
,即![]()
∴函数![]() 在区间
在区间![]() 上为减函数.
上为减函数.
(Ⅲ)解法1:∵当![]() 时,
时,![]()
![]()
当且仅当![]() ,即
,即![]() 时,“=”成立,
时,“=”成立,
∴函数![]() 在区间
在区间![]() 上的最小值为2.
上的最小值为2.
解法2:由![]() =0,
=0,![]() 得
得![]()
∵当![]() ,
,![]() ,∴
,∴![]() 即函数
即函数![]() 在区间
在区间![]() 上为增函数
上为增函数
∴![]() 是函数的最小值点,即函数
是函数的最小值点,即函数![]() 在
在![]() 取得最小值
取得最小值![]()
20.已知:函数![]() 在
在![]() 上有定义,
上有定义,![]() ,且对
,且对![]() 有
有![]() .
.
(Ⅰ)试判断函数![]() 的奇偶性;
的奇偶性;
(Ⅱ)对于数列![]() ,有
,有![]() 试证明数列
试证明数列![]() 成等比数列;
成等比数列;
(Ⅲ)求证:![]() .
.
解析:(Ⅰ)解:在![]() 中,令
中,令![]() 得
得![]()
再令![]() 得
得![]() ,∴
,∴![]()
∴![]() ,即函数
,即函数![]() 为奇函数
为奇函数
(Ⅱ)证明: 由![]() 得
得![]()
∵ 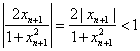 ∴
∴![]()
∴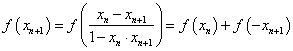
∵函数![]() 为奇函数,∴
为奇函数,∴ ![]() ,
,![]()
∵![]() 否则与
否则与![]() 矛盾,∴
矛盾,∴![]()
![]()
〔或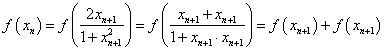 =2
=2![]() 〕
〕
∴![]() ,
,
∵![]() ∴
∴![]() 是以-1为首项,
是以-1为首项,![]() 为公比的等比数列
为公比的等比数列
(Ⅲ)证明:又(Ⅱ)可得![]()
∵![]() =
=![]()
![]()
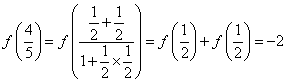
又∵![]() ∴
∴![]() ∴
∴![]()