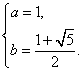高三第一学期期中数学考试卷(文科)(1)
第Ⅰ卷(选择题共55分)
一、选择题(本大题共11小题,每小题5分,共55分)
1、已知p:![]() ,
,![]() ; q:
; q:![]() ,
,![]() 。则p是q的
(
)
。则p是q的
(
)
A充分而不必要条件;B必要而不充分条件;C充要条件;D即不充分也不必要条件;
2、
设集合![]() ;则
;则![]() 等于()
等于()
A.![]() ; B. R;
C. {0} D.
; B. R;
C. {0} D.![]()
3、在等差数列![]() 中,
中,![]() ,
,![]() ,则
,则![]() 等于( )
等于( )
A.152 B .154 C.156 D.158
4、不等式![]() 的解集为
的解集为![]() ,则函数
,则函数![]() 的图象为()
的图象为()
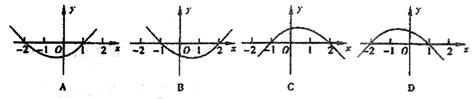
5、已知等差数列{an}的前n项和为Sn,且S2=10,S5=55,则过点P(n,an),Q(n+2,an+2)
(n∈N*)的直线的斜率为 ( )
| |
6、已知![]() 是定义在R上的奇函数,且
是定义在R上的奇函数,且![]() 的图象关于直线
的图象关于直线![]() 对称,则
对称,则
![]() ( )
( )
A.-2 B.–1 C.1 D.0
7、已知y = f(x)是偶函数,当x > 0时,f(x) = (x-1)2;若当![]() 时,n≤f(x)≤m恒成立,则m-n的最小值是 ( )
时,n≤f(x)≤m恒成立,则m-n的最小值是 ( )
A.![]() ; B.
; B.![]() ;
C. 1; D.
;
C. 1; D.![]()
8、 已知偶函数![]() 在
在![]() 上单调递减,若
上单调递减,若![]() ,
,![]() ,
,![]() ,
,
则![]() 之间的大小关系是
之间的大小关系是
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
9、设f(x)是定义在R上的偶函数,当![]() 时,
时,![]() 且f(1)=0,则不等式x·f(x)>0的解集为 ( )
且f(1)=0,则不等式x·f(x)>0的解集为 ( )
A.(-1,0)∪(1,+![]() ) B.(-1,0)∪(0,1)
) B.(-1,0)∪(0,1)
C.(-![]() ,-1)∪(1,+
,-1)∪(1,+![]() ) D.(-
) D.(-![]() ,-1)∪(0,1)
,-1)∪(0,1)
10、若![]() ,那么
,那么![]() 满足的条件是( )
满足的条件是( )
(A)![]() (B)
(B)![]() ; (C)
; (C)![]() ; (D)
; (D)![]()
11、在计算机的算法语言中有一种函数![]() 叫做取整函数(也称高斯函数),它表示
叫做取整函数(也称高斯函数),它表示![]() 的整数部分,即
的整数部分,即![]() 是不超过
是不超过![]() 的最大整数.例如:
的最大整数.例如:![]() .设函数
.设函数![]() ,则函数
,则函数![]() 的值域为 (
)
的值域为 (
)
(A)![]() (B)
(B)![]() (C)
(C) ![]() (D)
(D) ![]()
第Ⅱ卷(非选择题 共95分)
二、填空题(本大题共4小题,每小题4分,16共分)
12、已知:![]() ,
,![]() ,若
,若![]() 成立的一个充分不必要条件是
成立的一个充分不必要条件是![]() ,则实数
,则实数![]() 的取值范围
的取值范围
13、设![]() ,则
,则![]() 的值为
的值为
14、函数![]() 的单调递减区间为
的单调递减区间为
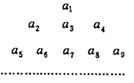 15、已知
15、已知![]() ,把数列{an}的各项排成如右图所示三角形形状,
,把数列{an}的各项排成如右图所示三角形形状,
记![]() 表示第m行、第n列的项,则
表示第m行、第n列的项,则![]() ______ ,
______ ,
a120在图中的位置为 .
三、解答题(本大题共6小题,共79分.解答应写出文字说明、证明过程或演算步骤)
16、(本小题满分10分)已知命题![]() :
:![]() 和
和![]() 是方程
是方程![]() 的两个实根,不等式
的两个实根,不等式![]() ,对任意实数
,对任意实数![]() 恒成立;命题
恒成立;命题![]() :只有一个实数
:只有一个实数![]() 满足不等式
满足不等式![]() ,若命题
,若命题![]() 是假命题,命题
是假命题,命题![]() 是真命题,求
是真命题,求![]() 的取值范围。
的取值范围。
17、(本小题满分14分)已知集合![]() 是满足下列性质的函数
是满足下列性质的函数![]() 的全体:在定义域内存在
的全体:在定义域内存在![]() ,使得
,使得![]() 成立.
成立.
(1)函数![]() 是否属于集合
是否属于集合![]() ?说明理由;
?说明理由;
(2)设函数![]() ,求
,求![]() 的取值范围;
的取值范围;
(3)证明:函数![]() .
.
18、 (本小题满分14分)已知数列![]() 的前
的前![]() 项和
项和![]() 满足
满足![]() ,且
,且![]()
![]()
(1)求k的值;
(2)求![]() ;
;
(3)是否存在正整数![]() ,使
,使![]() 成立?若存在,求出这样的正整数;若不存在,说明理由.
成立?若存在,求出这样的正整数;若不存在,说明理由.
19、 (本小题满分13分)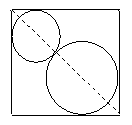 如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为
如图,在单位正方形内作两个互相外切的圆,同时每一个圆又与正方形的两相邻边相切,记其中一个圆的半径为![]() ,两圆的面积之和为
,两圆的面积之和为![]() ,将
,将![]() 表示为
表示为![]() 的函数,求函数
的函数,求函数![]() 的解析式及
的解析式及![]() 的值域.
的值域.
20、(本小题满分14分) 在数列![]() ,其前n项的和Sn满足关系式:
,其前n项的和Sn满足关系式:
![]()
![]() 。
。
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)求数列![]() 的公比为
的公比为![]() 作数列
作数列![]() ,使
,使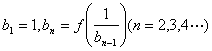 求bn
求bn
(3)求![]() 的值。
的值。
21、(本小题满分14分)![]() 是定义在R上的奇函数,当
是定义在R上的奇函数,当![]() 时,
时,![]() 。
。
(1)求![]() 时,
时,![]() 的解析式;
的解析式;
(2)问是否存在这样的正数![]() ,当
,当![]() 时,
时,![]() ,且
,且![]() 的值域为
的值域为![]()
若存在,求出所有的![]() 值,若不存在,请说明理由.
值,若不存在,请说明理由.
数学(文)试卷答案
一、选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 答案 | A | A | C | C | A | D | C | B | A | B | B |
二、填空题:12:![]() ; 13:6; 14:(-1,1);15:
; 13:6; 14:(-1,1);15:![]() ,
,![]() ;
;
三、解答题
16;解:(1)![]()
![]() 和
和![]() 是
是![]() 的两根,
的两根,
所以![]()
又![]() ,则有
,则有![]() 。因为不等式
。因为不等式![]() ,
,
对任意实数![]() 恒成立,所以
恒成立,所以![]() ,
,
所以![]()
![]() 由题意有
由题意有![]()
由命题“![]() 或
或![]() ”是假命题,命题“
”是假命题,命题“![]() 且
且![]() ”是假命题,有
”是假命题,有![]() 假
假![]() 假,所以
假,所以![]() 。
。
17;解:(1)若![]()
![]() ,则在定义域内存在
,则在定义域内存在![]() ,
,
使得![]() ,
,
∵方程![]() 无解,∴
无解,∴![]()
![]() .
.
![]() ,
,
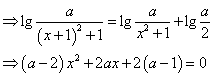
当![]() 时,
时,![]() ;
;
当![]() 时,由
时,由![]() ,得
,得![]() 。
。
∴![]() .
.
![]() ,
,
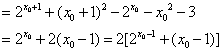
记![]() ,∵
,∵ ![]() ,
,![]() ,
,
∴ 即存在实数![]() ,使
,使![]() ,
,
令![]() ,则
,则![]() ,
,
∴
![]() ,即
,即![]() .
.
18;解:(1) ![]()
又![]() ,∴
,∴![]()
![]()
(2) 由 (1) 知 ![]() ①
①
当![]() 时,
时,![]() ②
②
①-②,得![]()
又![]() ,易见
,易见![]()
于是![]() 是等比数列,公比为
是等比数列,公比为![]() ,所以
,所以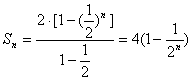
(3) 不等式![]() ,即
,即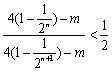 .
.
整理得![]()
假设存在正整数![]() 使得上面的不等式成立,由于2n为偶数,
使得上面的不等式成立,由于2n为偶数,![]() 为整数,
为整数,
则只能是![]()
![]()
因此,存在正整数![]() .
.
19;解:设另一个圆的半径为y,
则![]()
![]()
![]() ,
,
![]()
![]() ,
,
因为当一个圆为正方形内切圆时半径最大,而另一圆半径最小,
所以函数的定义域为![]()
因为![]() 所以
所以![]()
因为![]() 所以
所以![]() ;
;
所以函数![]() 的值域为
的值域为![]()
20;解:(1)由已知![]() ,即有
,即有
![]()
所以![]()
当![]() 时,有
时,有
![]() ①
①![]() ②
②
①—②得
![]() ;
; ![]()
综上所述,知![]()
![]()
因此![]() 是等比数列;
是等比数列;
(2)由(1)知![]() ;则使
;则使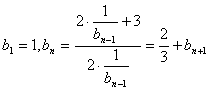
所以![]() ;因此,
;因此,![]() 是等差数列,
是等差数列,
且![]()
(3)![]()
![]()
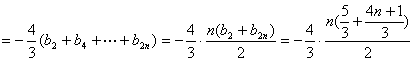
![]()
21;解:(1)设![]() ,则
,则![]() 于是
于是![]() ,
,
又![]() 为奇函数,所以
为奇函数,所以![]() ,即
,即![]() ,
,
(2)分下述三种情况:
①![]() 那么
那么![]() ,而当
,而当![]() 的最大值为1,
的最大值为1,
故此时不可能使![]() ,
,
②若![]() ,此时若
,此时若![]() ,则
,则![]() 的最大值为
的最大值为![]() ,得
,得![]() ,这与
,这与![]() 矛盾;
矛盾;
③若![]() ,因为
,因为![]() 时,
时,![]() 是减函数,则
是减函数,则![]() 于是有
于是有
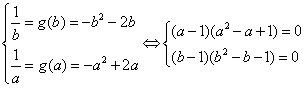
考虑到![]() 解得
解得![]() ;综上所述
;综上所述