![]() 必修5
第1章 解三角形
必修5
第1章 解三角形
§1.1正弦定理、余弦定理
重难点:理解正、余弦定理的证明,并能解决一些简单的三角形度量问题.
考纲要求:①掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.
经典例题:半径为R的圆外接于△ABC,且2R(sin2A-sin2C)=(![]() a-b)sinB.
a-b)sinB.
(1)求角C;
(2)求△ABC面积的最大值.
当堂练习:
1.在△ABC中,已知a=5, c=10, A=30°, 则∠B= ( )
(A) 105° (B) 60° (C) 15° (D) 105°或15°
2.在△ABC中,若a=2, b=2, c=+,则∠A的度数是 ( )
(A) 30° (B) 45° (C) 60° (D) 75°
3.在△ABC中,已知三边a、b、c 满足(a+b+c)·(a+b-c)=3ab, 则∠C=( )
(A) 15° (B) 30° (C) 45° (D) 60°
4.边长为5、7、8的三角形的最大角与最小角之和为 ( )
(A) 90° (B) 120° (C) 135° (D) 150°
5.在△ABC中,∠A=60°, a=, b=4, 那么满足条件的△ABC ( )
(A) 有 一个解 (B) 有两个解 (C) 无解 (D)不能确定
6.在平行四边形ABCD中,AC=BD, 那么锐角A的最大值为 ( )
(A) 30° (B) 45° (C) 60° (D) 75°
7. 在△ABC中,若![]() =
=![]() =
=![]() ,则△ABC的形状是
( )
,则△ABC的形状是
( )
(A) 等腰三角形 (B) 等边三角形 (C) 直角三角形 (D) 等腰直角三角形
8.如果把直角三角形的三边都增加同样的长度,则这个新的三角形的形状为( )
(A) 锐角三角形 (B) 直角三角形 (C) 钝角三角形 (D) 由增加的长度决定
9.在△ABC中,若a=50,b=25, A=45°则B= .
10.若平行四边形两条邻边的长度分别是4cm和4cm,它们的夹角是45°,则这个平行四边形的两条对角线的长度分别为 .
11.在等腰三角形 ABC中,已知sinA∶sinB=1∶2,底边BC=10,则△ABC的周长是 。
12.在△ABC中,若∠B=30°, AB=2, AC=2, 则△ABC的面积是 .
13.在锐角三角形中,边a、b是方程x2-2x+2=0的两根,角A、B满足2sin(A+B)-=0,求角C的度数,边c的长度及△ABC的面积。
14.在△ABC中,已知边c=10, 又知==,求a、b及△ABC的内切圆的半径。
15.已知在四边形ABCD中,BC=a,DC=2a,四个角A、B、C、D度数的比为3∶7∶4∶10,求AB的长。
16.在△ABC中,已知角A、B、C所对的边分别是a、b、c,边c=,且tanA+tanB=tanA·tanB-,又△ABC的面积为S△ABC=,求a+b的值。
![]() 必修5
第1章 解三角形
必修5
第1章 解三角形
§1.2正弦定理、余弦定理及其应用
考纲要求:①能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.
1. 有一长为1公里的斜坡,它的倾斜角为20°,现要将倾斜角改为10°,则坡底要伸长 ( )
A. 1公里 B. sin10°公里 C. cos10°公里 D. cos20°公里
2. 已知三角形的三边长分别为x2+x+1,x2-1和2x+1(x>1),则最大角为 ( )
A. 150° B. 120° C. 60° D. 75°
3.在△ABC中,![]() ,那么△ABC一定是 ( )
,那么△ABC一定是 ( )
A.锐角三角形 B.直角三角形
C.等腰三角形 D.等腰三角形或直角三角形
4.在△ABC中,一定成立的等式是 ( )
A.asinA=bsinB B.acosA=bcosB
C.asinB=bsinA D.acosB=bcosA
5.在△ABC中,A为锐角,lgb+lg(![]() )=lgsinA=-lg
)=lgsinA=-lg![]() , 则△ABC为 (
)
, 则△ABC为 (
)
A. 等腰三角形 B. 等边三角形
C. 直角三角形 D. 等腰直角三角形
6.在△ABC中,![]() ,则△ABC 的面积为 (
)
,则△ABC 的面积为 (
)
A. ![]() B.
B.
![]() C.
C.
![]() D.
1
D.
1
7.若![]() 则△ABC为 (
)
则△ABC为 (
)
A.等边三角形 B.等腰三角形
C.有一个内角为30°的直角三角形 D.有一个内角为30°的等腰三角形
8.边长为5、7、8的三角形的最大角与最小角之和的 ( )
A. 90° B. 120° C. 135° D. 150°
9.在△ABC中,根据下列条件解三角形,则其中有两个解的是 ( )
A.b = 10,A = 45°,B = 70° B.a = 60,c = 48,B = 100°
C.a = 7,b = 5,A = 80° D.a = 14,b = 16,A = 45°
10.在三角形ABC中,已知A![]() ,b=1,其面积为
,b=1,其面积为![]() ,则
,则![]() 为 ( )
为 ( )
A.![]() B.
B. ![]() C.
C.
![]() D.
D. ![]()
11.某人站在山顶向下看一列车队向山脚驶来,他看见第一辆车与第二辆车的俯角差等于他看见第二辆车与第三辆车的俯角差,则第一辆车与第二辆车的距离![]() 与第二辆车与第三辆车的距离
与第二辆车与第三辆车的距离![]() 之间的关系为
( )
之间的关系为
( )
A. ![]() B.
B. ![]()
C. ![]() D.
不能确定大小
D.
不能确定大小
12.在200米高的山顶上,测得山下一塔顶与塔底的俯角分别为30°、60°,则塔高为( )
A. ![]() 米 B.
米 B.
![]() 米
米
C. 200![]() 米 D.
200米
米 D.
200米
13. 在△ABC中,若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
14. 在△ABC中,B=1350,C=150,a=5,则此三角形的最大边长为 .
15. 在锐角△ABC中,已知![]() ,则的
,则的![]() 取值范围是
.
取值范围是
.
16. 在△ABC中,已知AB=4,AC=7,BC边的中线![]() ,那么BC= .
,那么BC= .
17. 已知锐角三角形的三边长分别为2、3、![]() ,则
,则![]() 的取值范围是 .
的取值范围是 .
18. 在△ABC中,已知![]() ,
,![]() ,则其最长边与最短边的比为 .
,则其最长边与最短边的比为 .
19.为了测量上海东方明珠的高度,某人站在A处测得塔尖的仰角为![]() ,前进38.5m后,到达B处测得塔尖的仰角为
,前进38.5m后,到达B处测得塔尖的仰角为![]() .试计算东方明珠塔的高度(精确到1m).
.试计算东方明珠塔的高度(精确到1m).
20.在![]() 中,已知
中,已知![]() ,判定
,判定![]() 的形状.
的形状.
21.在△ABC中,最大角A为最小角C的2倍 ,且三边a、b、c为三个连续整数,求a、b、c的值.
22.在△ABC中,若![]() ,试求
,试求![]() 的值.
的值.
23. 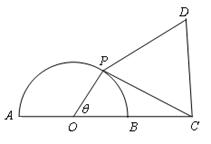 如图,已知
如图,已知![]() 的半径为1,点C在直径AB的延长线上,BC=1,点P是
的半径为1,点C在直径AB的延长线上,BC=1,点P是![]() 上半圆上的一个动点,以PC为边作正三角形PCD,且点D
上半圆上的一个动点,以PC为边作正三角形PCD,且点D
与圆心分别在PC两侧.
(1)若![]() ,试将四边形OPDC的面积
,试将四边形OPDC的面积
y表示成![]() 的函数;
的函数;
(2)求四边形OPDC面积的最大值.
![]() 必修5
第2章 数列
必修5
第2章 数列
§2.1数列的概念与简单表示
重难点:理解数列的概念,认识数列是反映自然规律的基本数学模型,探索并掌握数列的几种间单的表示法(列表、图象、通项公式);了解数列是一种特殊的函数;发现数列规律找出可能的通项公式.
考纲要求:①了解数列的概念和几种简单的表示方法(列表、图像、通项公式).
②了解数列是自变量巍峨正整数的一类函数.
经典例题:假设你正在某公司打工,根据表现,老板给你两个加薪的方案:(Ⅰ)每年年末加1000元;(Ⅱ)每半年结束时加300元。请你选择:(1)如果在该公司干10年,问两种方案各加薪多少元? (2)对于你而言,你会选择其中的哪一种?
当堂练习:
1. 下列说法中,正确的是 ( )
A.数列1,2,3与数列3,2,1是同一个数列.
B.数列l, 2,3与数列1,2,3,4是同一个数列.
C.数列1,2,3,4,…的一个通项公式是an=n.
D.以上说法均不正确.
2.巳知数列{ an}的首项a1=1,且an+1=2 an+1,(n≥2),则a5为 ( )
A.7. B.15 C.30 D.31.
3.数列{ an}的前n项和为Sn=2n2+1,则a1,a5的值依次为 ( )
A.2,14 B.2,18 C.3,4. D.3,18.
4.已知数列{ an}的前n项和为Sn=4n2 -n+2,则该数列的通项公式为 ( )
A. an=8n+5(n∈N*) B. an=8n-5(n∈N*)
C. an=8n+5(n≥2) D. 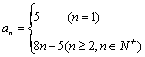
5.已知数列{ an}的前n项和公式Sn=n2+2n+5,则a6+a7+a8= ( )
A.40. B.45 C.50 D.55.
6.若数列![]() 前8项的值各异,且
前8项的值各异,且![]() 对任意的
对任意的![]() 都成立,则下列数列中可取遍
都成立,则下列数列中可取遍![]() 前8项值的数列为 ( )
前8项值的数列为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.在数列{ an}中,已知an=2,an= an+2n,则a4 +a6 +a8的值为 .
8.已知数列{ an}满足a1=1 , an+1=c an+b, 且a2 =3,a4=15,则常数c,b 的值为 .
9.已知数列{ an}的前n项和公式Sn=n2+2n+5,则a6+a7+a8= .
10.设![]() 是首项为1的正项数列,且
是首项为1的正项数列,且![]() (
(![]() =1,2,3,…),则它的通项公式是
=1,2,3,…),则它的通项公式是![]() =________.
=________.
11. 下面分别是数列{ an}的前n项和an的公式,求数列{ an}的通项公式:
(1)Sn=2n2-3n; (2)Sn=3n-2
12. 已知数列{ an}中a1=1,![]() (1)写出数列的前5项;(2)猜想数列的通项公式.
(1)写出数列的前5项;(2)猜想数列的通项公式.
13. 已知数列{ an}满足a1=0,an+1+Sn=n2+2n(n∈N*),其中Sn为{ an}的前n项和,求此数列的通项公式.
14. 已知数列{ an}的通项公式an与前n项和公式Sn之间满足关系Sn=2-3an
(1)求a1;
(2)求an与an (n≥2,n∈N*)的递推关系;
(3)求Sn与Sn (n≥2,n∈N*)的递推关系,
![]() 必修5
第2章 数列
必修5
第2章 数列
§2.2等差数列、等比数列
重难点:理解等差数列、等比数列的概念,掌握等差数列、等比数列的通项公式与前![]() 项和公式,能在具体的问题情境中,识别数列的等差关系或等比关系,并能用有关知识解决相应的问题.
项和公式,能在具体的问题情境中,识别数列的等差关系或等比关系,并能用有关知识解决相应的问题.
考纲要求:①理解等差数列、等比数列的概念.
②掌握等差数列、等比数列的通项公式与前![]() 项和公式.
项和公式.
③能在具体的问题情境中,识别数列的等差关系或等比关系,并能用有关知识解决相应的问题.
④了解等差数列与一次函数、等比数列与指数函数的关系.
经典例题:已知一个数列{an}的各项是1或3.首项为1,且在第k个1和第k+1个1之间有2k-1个3,即1,3,1,3,3,3,1,3,3,3,3,3,1,…,记该数列的前n项的和为Sn.
(1)试问第2006个1为该数列的第几项?
(2)求a2006;
(3)求该数列的前2006项的和S2006;
当堂练习:
1.数列![]() 则
则![]() 是该数列的( )
是该数列的( )
A.第6项 B.第7项 C.第10项 D.第11项
2.方程![]() 的两根的等比中项是( )
的两根的等比中项是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3. 已知![]() 为各项都大于零的等比数列,公比
为各项都大于零的等比数列,公比![]() ,则( )
,则( )
A.![]() B.
B.![]()
C.![]() D.
D.![]() 和
和![]() 的大小关系不能由已知条件确定
的大小关系不能由已知条件确定
4.一个有限项的等差数列,前4项之和为40,最后4项之和是80,所有项之和是210,则此数列的项数为( )
A.12
B.![]() C.16
D.18
C.16
D.18
5.若a、b、c成等差数列,b、c、d成等比数列,![]() 成等差数列,则a、c、e成( )
成等差数列,则a、c、e成( )
A.等差数列 B.等比数列
C.既成等差数列又成等比数列 D.以上答案都不是
6.在等差数列{an}中,![]() ,则
,则![]() ( )
( )
A.4 B.![]() C.8 D.
C.8 D.![]()
7.两等差数列{an}、{bn}的前n项和的比![]() ,则
,则![]() 的值是( )
的值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.{an}是等差数列,![]() ,则使
,则使![]() 的最小的n值是( )
的最小的n值是( )
A.5 B.![]() C.7 D.8
C.7 D.8
9.{an}是实数构成的等比数列,![]() 是其前n项和,则数列{
是其前n项和,则数列{![]() } 中( )
} 中( )
A.任一项均不为0 B.必有一项为0
C.至多有一项为0 D.或无一项为0,或无穷多项为0
10.某数列既成等差数列也成等比数列,那么该数列一定是( )
A.公差为0的等差数列 B.公比为1的等比数列
C.常数数列![]() D.以上都不对
D.以上都不对
11.已知等差数列{an}的公差d≠0,且a1、a3、a9成等比数列,则![]() 的值是 .
的值是 .
12.由正数构成的等比数列{an},若![]() ,则
,则![]() .
.
13.已知数列{an}中,![]() 对任意正整数n都成立,且
对任意正整数n都成立,且![]() ,则
,则![]() .
.
14.在等差数列{an}中,若![]() ,则有等式
,则有等式![]() 成立,类比上述性质,相应地:在等比数列{bn}中,若
成立,类比上述性质,相应地:在等比数列{bn}中,若![]() ,则有等式
,则有等式
15. 已知数列{2n-1an }的前n项和![]() .
.
⑴求数列{an}的通项公式;⑵设![]() ,求数列
,求数列![]() 的前n项和.
的前n项和.
16.已知数列{an}是等差数列,且![]() .
.
⑴求数列{an}的通项公式;⑵令![]() ,求数列{bn}前n项和的公式.
,求数列{bn}前n项和的公式.
17. 甲、乙两人连续6年对某县农村养鸡业规模进行调查,提供两个不同的信息图如图所示.甲调查表明:从第1年每个养鸡场出产1万只鸡上升到第6年平均每个鸡场出产2万只鸡.乙调查表明:由第1年养鸡场个数30个减少到第6年10个.
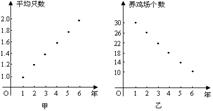 请您根据提供的信息说明:
请您根据提供的信息说明:
⑴第2年养鸡场的个数及全县出产鸡的总只数;
⑵到第6年这个县的养鸡业比第1年是扩大了还是
缩小了?请说明理由;
⑶哪一年的规模最大?请说明理由.
18.已知数列{an}为等差数列,公差![]() ,{an}的部分项组成的数列
,{an}的部分项组成的数列![]() 恰为等比数列,其中
恰为等比数列,其中![]() ,求
,求![]() .
.
![]() 必修5 第2章 数列
必修5 第2章 数列
§2.3等差数列、等比数列综合运用
1、设![]() 是等比数列,有下列四个命题:①
是等比数列,有下列四个命题:①![]() 是等比数列;②
是等比数列;②![]() 是等比数列;
是等比数列;
③![]() 是等比数列;④
是等比数列;④![]() 是等比数列。其中正确命题的个数是
( )
是等比数列。其中正确命题的个数是
( )
A、1 B、2 C、3 D、4
2、![]() 为等比数列,公比为
为等比数列,公比为![]() ,则数列
,则数列![]() 是( )
是( )
A、公比为![]() 的等比数列
B、公比为
的等比数列
B、公比为![]() 的等比数列
的等比数列
C、公比为![]() 的等比数列
D、公比为
的等比数列
D、公比为![]() 的等比数列
的等比数列
3、已知等差数列![]() 满足
满足![]() ,则有
(
)
,则有
(
)
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
4、若直角三角形的三边的长组成公差为3的等差数列,则三边的长分别为 ( )
A、5,8,11 B、9,12,15 C、10,13,16 D、15,18,21
5、数列![]() 必为
(
)
必为
(
)
A、等差非等比数列 B、等比非等差数列 C、既等差且等比数列 D、以上都不正确
6、若一个等差数列前3项的和为34,最后3项的和为146,且所有项的和为390,则这个
数列共有 A、10项 B、11项 C、12项 D、13项 ( )
7、在等差数列![]() 中,
中,![]() ,且
,且![]() 成等比数列,则
成等比数列,则![]() 的通项公式为 ( )
的通项公式为 ( )
A、![]() B、
B、![]() C、
C、![]() 或
或![]() D、
D、![]() 或
或![]()
8、数列![]() 的前
的前![]() 项的和为
(
)
项的和为
(
)
A、![]() B、
B、![]() C、
C、![]() D、以上均不正确
D、以上均不正确
9、等差数列![]() 中,
中,![]() ,则前10项的和
,则前10项的和![]() 等于
(
)
等于
(
)
A、720 B、257 C、255 D、不确定
10、某人于2000年7月1日去银行存款![]() 元,存的是一年定期储蓄;2001年7月1日他将
元,存的是一年定期储蓄;2001年7月1日他将
到期存款的本息一起取出,再加![]() 元后,还存一年的定期储蓄,此后每年7月1日他都
元后,还存一年的定期储蓄,此后每年7月1日他都
按照同样的方法,在银行存款和取款;设银行一年定期储蓄利率![]() 不变,则到2005年
不变,则到2005年
7月1日,他将所有的存款和利息全部取出时,取出的钱数共有多少元? ( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
11、在某报《自测健康状况》的报道中,自测血压结果与相应年龄的统计数据如下表,
观察表中的数列的特点,用适当的数填入表中空格内:
| 年龄(岁) | 30 | 35 | 40 | 45 | 50 | 55 | 60 | 65 |
| 收缩压(水银柱,毫米) | 110 | 115 | 120 | 125 | 130 | 135 | 145 | |
| 舒张压 | 70 | 73 | 75 | 78 | 80 | 83 | 88 |
12、两个数列![]() 与
与![]() 都成等差数列,且
都成等差数列,且![]() ,则
,则![]() =
=
13、公差不为0的等差数列的第2,3,6项依次构成一等比数列,该等比数列的公比![]() =
=
14、等比数列![]() 中,
中,![]() ,前
,前![]() 项和为
项和为![]() ,满足
,满足![]() 的最小自然数
的最小自然数![]() 为
为
15、设![]() 是一个公差为
是一个公差为![]() 的等差数列,它的前10项和
的等差数列,它的前10项和![]() ,且
,且![]()
成等比数列.(1)证明![]() ;(2)求公差
;(2)求公差![]() 的值和数列
的值和数列![]() 的通项公式.
的通项公式.
16、(1)在等差数列![]() 中,
中,![]() ,求
,求![]() 及前
及前![]() 项和
项和![]() ;
;
(2)在等比数列![]() 中,
中,![]() ,求
,求![]() .
.
17、设无穷等差数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)若首项![]() ,公差
,公差![]() ,求满足
,求满足![]() 的正整数
的正整数![]() ;
;
(2)求所有的无穷等差数列![]() ,使得对于一切正整数
,使得对于一切正整数![]() 都有
都有![]() 成立.
成立.
18.甲、乙两大型超市,2001年的销售额均为P(2001年为第1年),根据市场分析和预测,甲超市前n年的总销售额为![]() ,乙超市第n年的销售额比前一年多
,乙超市第n年的销售额比前一年多![]() .
.
(I)求甲、乙两超市第n年的销售额的表达式;
(II)根据甲、乙两超市所在地的市场规律,如果某超市的年销售额不足另一超市的年销售额的20%,则该超市将被另一超市收购,试判断哪一个超市将被收购,这个情况将在哪一年出现,试说明理由.
![]() 必修5
第2章 数列
必修5
第2章 数列
数列单元检测
1. 已知等差数列![]() 的前n项和为Sn,若
的前n项和为Sn,若![]() 等于
( D
)
等于
( D
)
A.18 B.36
C.54 D.72
2. 已知![]() 为等差数列,
为等差数列,![]() 为等比数列,其公比
为等比数列,其公比![]() ,且
,且![]() ,若
,若![]() ,
,![]() ,则
( B )
,则
( B )
A.![]() B.
B.![]()
C.![]() D.
D.![]() 或
或![]()
3. 在等差数列{a![]() }中,3(a
}中,3(a![]() +a
+a![]() )+2(a
)+2(a![]() +a
+a![]() +a
+a![]() )=24,则此数列的前13项之和为 ( D
)
)=24,则此数列的前13项之和为 ( D
)
A.156 B.13
C.12 D.26
4. 已知正项等比数列数列{an},bn=log a an, 则数列{bn}是 ( A )
A、等比数列 B、等差数列
C、既是等差数列又是等比数列 D、以上都不对
5. 数列![]() 是公差不为零的等差数列,并且
是公差不为零的等差数列,并且![]() 是等比数列
是等比数列![]() 的相邻三项,若
的相邻三项,若![]() ,则
,则![]() 等于
(
B )
等于
(
B )
A. ![]() B.
B.
![]()
C.![]() D.
D. ![]()
6. 数列1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,…的第1000项的值是 ( B )
A. 42 B.45 C. 48 D. 51
7. 一懂n层大楼,各层均可召集n个人开会,现每层指定一人到第k层开会,为使n位开会人员上下楼梯所走路程总和最短,则k应取 ( D )
A.![]() n B.
n B.![]() (n—1)
C.
(n—1)
C.![]() (n+1)
(n+1)
D.n为奇数时,k=![]() (n—1)或k=
(n—1)或k=![]() (n+1),n为偶数时k=
(n+1),n为偶数时k=![]() n
n
8. 设数列![]() 是等差数列,
是等差数列,![]()
![]() ,Sn是数列
,Sn是数列![]() 的前n项和,则( B )
的前n项和,则( B )
A.S4<S5 B.S4=S5 C.S6<S5 D.S6=S5
9. 等比数列![]() 的首项
的首项![]() ,前
,前![]() 项和为
项和为![]() 若
若![]() ,则公比
,则公比![]() 等于 ( B )
等于 ( B )
![]() C.2
D.-2
C.2
D.-2
10. 已知Sn是等差数列{an}的前n项和,若S6=36,Sn=324,Sn-6=144(n>6),则n等于 ( D )
A.15 B.16 C.17 D.18
11. 已知![]() ,(
,(![]() ),则在数列{
),则在数列{![]() }的前50项中最小项和最大项分别是( C )
}的前50项中最小项和最大项分别是( C )
A.![]() B.
B.![]() C.
C.
![]() D.
D.![]()
12. 已知:![]() ,若称使乘积
,若称使乘积![]() 为整数的数n为劣数,
为整数的数n为劣数,
则在区间(1,2002)内所有的劣数的和为 ( A )
A.2026 B.2046
C.1024 D.1022
13. 在等差数列![]() 中,已知a1+a3+a5=18,
an-4+an-2+an=108,Sn=420,则n= .
中,已知a1+a3+a5=18,
an-4+an-2+an=108,Sn=420,则n= .
14. 在等差数列![]() 中,公差
中,公差![]() ,且
,且![]() ,则
,则![]() (k∈N+,
(k∈N+,
k≤60)的值为 .
15. 已知![]() 则 通项公式
则 通项公式![]() =
.
=
.
16. 已知![]() ,则
,则![]() =
;
=
; ![]() =
.
=
.
17. 若数列![]() 前n项和可表示为
前n项和可表示为![]() ,则
,则![]() 是否可能成为等比数列?若可能,求出a值;若不可能,说明理由.
是否可能成为等比数列?若可能,求出a值;若不可能,说明理由.
18.设{an}为等差数列,{bn}为等比数列,a1=b1=1,a2+a4=b3,b2·b4=a3,分别求出{an}及{bn}的前n项和S10及T10.
19.已知数列{an}是公比为q的等比数列,Sn是其前n项和,且S3,S9,S6成等差数列
(1)求证:a2 , a8, a5也成等差数列
(2)判断以a2, a8, a5为前三项的等差数列的第四项是否也是数列{an}中的一项,若是求出这一项,若不是请说明理由.
20.等比数列![]() 的首项为
的首项为![]() ,公比为
,公比为![]() ,用
,用![]() 表示这个数列的第n项到第m项共
表示这个数列的第n项到第m项共![]() 项的和.
项的和.
(Ⅰ)计算![]() ,
,![]() ,
,![]() ,并证明它们仍成等比数列;
,并证明它们仍成等比数列;
(Ⅱ)受上面(Ⅰ)的启发,你能发现更一般的规律吗?写出你发现的一般规律,并证明.
21.某城市2001年末汽车保有量为30万辆,预计此后每年报废上一年末汽车保有量的6%,并且每年新增汽车数量相同.为保护城市环境,要求该城市汽车保有量不超过60万辆,那么每年新增汽车数量不应超过多少辆?
![]() 必修5
第3章 不等式
必修5
第3章 不等式
§3.1-2不等关系、一元二次不等式
重难点:通过具体情境,能建立不等式模型;掌握一元二次不等式解法,理解一元二次不等式、一元二次方程、二次函数之间关系并能灵活运用.
考纲要求:①了解现实世界和日常生活中的不等关系,了解不等式(组)的实际背景.
②会从实际情境中抽象出一元二次不等式模型.
③通过函数图像了解一元二次不等式与相应的二次函数、一元二次方程的联系.
④会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图.
经典例题:某种牌号的汽车在水泥路面上的刹车Sm和汽车车速![]() km/h有如下关系:
km/h有如下关系:![]() ,在一次交通事故中,测得这种车的刹车距离大于39.5m,那么这辆汽车刹车前的车速至少为多少?(精确到0.01km/h).
,在一次交通事故中,测得这种车的刹车距离大于39.5m,那么这辆汽车刹车前的车速至少为多少?(精确到0.01km/h).
当堂练习:
1、
1. 方程![]() 有两个不相等的实数根,则实数m的取值范围是( )
有两个不相等的实数根,则实数m的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2. 下列各一元二次不等式中,解集为空集的是(
)![]()
A.(x+3)(x-1)>0 B.(x+4)(x-1)<0 C.x2-2x+3<0 D.2x2-3x-2>0
3. 不等式组![]() 的解集为( )
的解集为( )
A.(-∞,-2]∪[3,4) B.(-∞,-2]∪(4,+∞)
C.(4,+∞) D.(-∞,-2]∪(4,+∞)
4. 若0<a<1,则不等式![]() 的解是( )
的解是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
5. 若![]() ,则
,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.3
D.
C.3
D.![]()
6. 一元二次不等式ax![]() +bx+2
+bx+2![]() 0的解集是(-
0的解集是(-![]() ,
, ![]() ),则a+b的值是( )
),则a+b的值是( )
A.10 B.-10 C.14 D.-14
7. 若0<a<1,则不等式(x-a)(x-![]() )>0的解集是( )
)>0的解集是( )
A.(a,![]() ) B.(
) B.(![]() ,a)
,a)
C.(-∞,a)∪(![]() ,+∞) D.(-∞,
,+∞) D.(-∞,![]() )∪(a,+∞)
)∪(a,+∞)
8. 若不等式![]() 的解集为
的解集为![]() ,则下列结论中正确的是( )
,则下列结论中正确的是( )
A. ![]() B.
B. ![]()
C. ![]() D.
D.![]()
9. 己知关于x的方程(m+3)x 2-4mx +2m-1= 0 的两根异号,且负根的绝对值比正根大,那么实数m的取值范围是( )
A.-3< m<0 B.0<m<3
C.m<-3或m> 0 D.m<0 或 m>3
10. 有如下几个命题:
①如果x1, x2是方程ax2+bx+c=0的两个实根且x1<x2,那么不等式ax2+bx+c<0的解集为{x∣x1<x<x2};
②当Δ=b2-4ac<0时,二次不等式 ax2+bx+c>0的解集为![]() ;
;
③![]() 与不等式(x-a)(x-b)≤0的解集相同;
与不等式(x-a)(x-b)≤0的解集相同;
④![]() 与x2-2x<3(x-1)的解集相同.
与x2-2x<3(x-1)的解集相同.
其中正确命题的个数是( )
A.3 B.2 C.1 D.0
11. 函数![]() 的定义域是
.
的定义域是
.
12. 已知关于x的不等式![]() 对
对![]() R恒成立,则t的取值范围是
.
R恒成立,则t的取值范围是
.
13. 若不等式![]() 的解集为
的解集为![]() ,则实数p= .
,则实数p= .
14. ![]() 和
和![]() 是关于x的方程x2-(k-2)x+k2+3k+5=0的两个实根,则
是关于x的方程x2-(k-2)x+k2+3k+5=0的两个实根,则![]() 2+
2+![]() 2的最大值为 .
2的最大值为 .
15. 设![]() ,解关于
,解关于![]() 的不等式:
的不等式:![]()
16. 已知函数y=(k2+4k-5)x2+4(1-k)x+3的图像都在x轴上方,求实数k的取值范围.
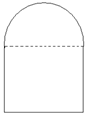
17. 要在墙上开一个上半部为半圆形、下部为矩形的窗户(如图所示),在窗框为定长的条件下,要使窗户能够透过最多的光线,窗户应设计成怎样的尺寸?
18. 设A={xx2 +3k2≥2k(2x-1)},B={xx2-(2x-1)k+k2≥0}且A![]() B,试求k的取值范围.
B,试求k的取值范围.
![]() 必修5
第3章 不等式
必修5
第3章 不等式
§3.3二元一次不等式组与简单的线性规划问题
重难点:会从实际情境中抽象出二元一次不等式组;了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组;会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决.
考纲要求:①会从实际情境中抽象出二元一次不等式组.
②了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组.
③会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决.
经典例题:求不等式x-2+y-2≤2所表示的平面区域的面积.
当堂练习:
1.下列各点中,与点(1,2)位于直线x+y-1=0的同一侧的是 ( )
A.(0,0) B.(-1,1) C.(-1,3) D.(2,-3)
2.下列各点中,位于不等式(x+2y+1)(x-y+4)<0表示的平面区域内的是 ( )
A.(0,0) B.(-2,0) C.(-1,0) D.(2,3)
3.用不等式组表示以点(0,0)、(2,0)、(0,-2)为顶点的三角形内部,该不等式组为_______.
4.甲、乙两地生产某种产品,它们可调出的数量分别是300t和750t.A、B、C三地需要该种产品的数量分别为200t、450t、400t,甲运往A、B、C三地每1t产品的运费分别为6元、3元、5元,乙地运往A、B、C三地每1t产品的运费分别为5元、9元、6元,为使运费最低,调运方案是_______,最低运费是_______.
5.画出不等式组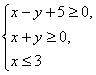 表示的平面区域.
表示的平面区域.
6.一个农民有田2亩,根据他的经验,若种水稻,则每亩每期产量为400千克;若种花生,则每亩每期产量为100千克,但水稻成本较高,每亩每期需240元,而花生只要80元,且花生每千克可卖5元,稻米每千克只卖3元,现在他只能凑足400元,问这位农民对两种作物各种多少亩,才能得到最大利润?
7.已知-4≤a-b≤-1,-1≤4a-b≤5,求9a-b的取值范围.
8.给出的平面区域是△ABC内部及边界(如下图),若目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,求a的值及z的最大值.
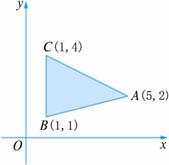
9.若把满足二元二次不等式(组)的平面区域叫做二次平面域.
(1)画出9x2-16y2+144≤0对应的二次平面域;
(2)求x2+y2的最小值;
(3)求![]() 的取值范围.
的取值范围.
![]() 必修5
第3章 不等式
必修5
第3章 不等式
§3.4基本不等式
重难点:了解基本不等式的证明过程;会用基本不等式解决简单的最大(小)值问题.
考纲要求:①了解基本不等式的证明过程.
②会用基本不等式解决简单的最大(小)值问题.
经典例题:若a,b,c都是小于1的正数,求证:![]() ,
,![]() ,
,![]() 不可能同时大于
不可能同时大于![]() .
.
1. 若![]()
![]() ,下列不等式恒成立的是 ( )
,下列不等式恒成立的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2. 若![]() 且
且![]() ,则下列四个数中最大的是 ( )
,则下列四个数中最大的是 ( )
A.![]() B.
B.![]()
![]() C.2ab D.a
C.2ab D.a
3. 设x>0,则![]() 的最大值为
( )
的最大值为
( )
A.3 B.![]() C.
C.![]()
![]() D.-1
D.-1
4. 设![]() 的最小值是( )
的最小值是( )
A. 10
B. ![]() C.
C. ![]() D.
D. ![]()
5. 若x, y是正数,且![]() ,则xy有 ( )
,则xy有 ( )
A.最大值16 B.最小值![]() C.最小值16 D.最大值
C.最小值16 D.最大值![]()
6. 若a, b, c∈R,且ab+bc+ca=1, 则下列不等式成立的是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
7. 若x>0, y>0,且x+y![]() 4,则下列不等式中恒成立的是
(
)
4,则下列不等式中恒成立的是
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8. a,b是正数,则![]() 三个数的大小顺序是 ( )
三个数的大小顺序是 ( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9. 某产品的产量第一年的增长率为p,第二年的增长率为q,设这两年平均增长率为x,则有( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10. 下列函数中,最小值为4的是 ( )
A.![]() B.
B.![]()
![]()
C.![]() D.
D.![]()
![]()
11. 函数![]() 的最大值为 .
的最大值为 .
12. 建造一个容积为18m3, 深为2m的长方形无盖水池,如果池底和池壁每m2 的造价为200元和150元,那么池的最低造价为 元.
13. 若直角三角形斜边长是1,则其内切圆半径的最大值是 .
14. 若x, y为非零实数,代数式![]() 的值恒为正,对吗?答 .
的值恒为正,对吗?答 .
15. 已知:![]() , 求mx+ny的最大值.
, 求mx+ny的最大值.
16. 已知![]() .若
.若![]() 、
、![]() , 试比较
, 试比较![]() 与
与![]() 的大小,并加以证明.
的大小,并加以证明.
17. 已知正数a, b满足a+b=1(1)求ab的取值范围;(2)求![]() 的最小值.
的最小值.
18. 设![]() .证明不等式
.证明不等式 ![]() 对所有的正整数n都成立.
对所有的正整数n都成立.
![]() 必修5
第3章 不等式
必修5
第3章 不等式
§3.5不等式单元测试
1.设![]() ,
,![]() ,则下列不等式中一定成立的是 ( )
,则下列不等式中一定成立的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2. “![]() ”是“
”是“![]() ”的 ( )
”的 ( )
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.既不充分也不必要条件
3.不等式![]() 的解集不可能是 ( )
的解集不可能是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.不等式![]() 的解集是
的解集是![]() ,则
,则![]() 的值等于 ( )
的值等于 ( )
A.-14 B.14 C.-10 D.10
5.不等式![]() 的解集是 ( )
的解集是 ( )
A.![]() B.
B.![]()
C.![]() 或
或![]() D.
D.![]()
6.若![]() ,则下列结论不正确的是 ( )
,则下列结论不正确的是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若![]() ,
,![]() ,则
,则![]() 与
与![]() 的大小关系为 ( )
的大小关系为 ( )
A.![]() B.
B.![]() C.
C.![]() D.随x值变化而变化
D.随x值变化而变化
8.下列各式中最小值是2的是 ( )
A.![]() +
+![]() B.
B.![]() C.tanx+cotx D.
C.tanx+cotx D. ![]()
9.下列各组不等式中,同解的一组是 ( )
A.![]() 与
与![]() B.
B.![]() 与
与![]()
C.![]() 与
与![]() D.
D.![]() 与
与![]()
10.如果![]() 对任意实数x总成立,则a的取值范围是 ( )
对任意实数x总成立,则a的取值范围是 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
11.若![]() ,则
,则![]() 与
与![]() 的大小关系是
.
的大小关系是
.
12.函数![]() 的定义域是
.
的定义域是
.
13.某公司一年购买某种货物400吨,每次都购买![]() 吨,运费为4万元/次,一年的总存储费用为
吨,运费为4万元/次,一年的总存储费用为![]() 万元,要使一年的总运费与总存储费用之和最小,则
万元,要使一年的总运费与总存储费用之和最小,则![]() 吨.
吨.
14. 已知![]() , 则不等式
, 则不等式![]() 的解集___ _ ____.
的解集___ _ ____.
15.已知![]() 是奇函数,且在(-
是奇函数,且在(-![]() ,0)上是增函数,
,0)上是增函数,![]() ,则不等式
,则不等式![]() 的解集是___ _ ____.
的解集是___ _ ____.
16.解不等式:![]()
17.已知![]() ,解关于
,解关于![]() 的不等式
的不等式![]() .
.
18.已知![]() ,求证:
,求证:![]() 。
。
19.对任意![]() ,函数
,函数![]() 的值恒大于零,求
的值恒大于零,求![]() 的取值范围。
的取值范围。
20.如图所示,校园内计划修建一个矩形花坛并在花坛内装置两个相同的喷水器。已知喷水器的喷水区域是半径为5m的圆。问如何设计花坛的尺寸和两个喷水器的位置,才能使花坛的面积最大且能全部喷到水?
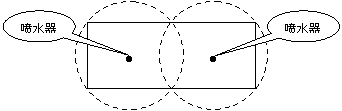 |
21.已知函数![]() .
.
(1)若对任意的实数![]() ,都有
,都有![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)当![]() 时,
时,![]() 的最大值为M,求证:
的最大值为M,求证:![]() ;
;
(3)若![]() ,求证:对于任意的
,求证:对于任意的![]() ,
,![]() 的充要条件是
的充要条件是![]()
![]() 必修5
必修5综合测试
必修5
必修5综合测试
1.如果![]() ,那么
,那么![]() 的最小值是( )
的最小值是( )
A.4 B.![]() C.9 D.18
C.9 D.18
2、数列![]() 的通项为
的通项为![]() =
=![]() ,
,![]() ,其前
,其前![]() 项和为
项和为![]() ,则使
,则使![]() >48成立的
>48成立的![]() 的最小值为( )
的最小值为( )
A.7 B.8 C.9 D.10
3、若不等式![]() 和不等式
和不等式![]() 的解集相同,则
的解集相同,则![]() 、
、![]() 的值为( )
的值为( )
A.![]() =﹣8
=﹣8 ![]() =﹣10 B.
=﹣10 B.![]() =﹣4
=﹣4 ![]() =﹣9 C.
=﹣9 C.![]() =﹣1
=﹣1 ![]() =9 D.
=9 D.![]() =﹣1
=﹣1 ![]() =2
=2
4、△ABC中,若![]() ,则△ABC的形状为( )
,则△ABC的形状为( )
A.直角三角形 B.等腰三角形 C.等边三角形 D.锐角三角形
5、在首项为21,公比为![]() 的等比数列中,最接近1的项是( )
的等比数列中,最接近1的项是( )
A.第三项 B.第四项 C.第五项 D.第六项
6、在等比数列![]() 中,
中,![]() =6,
=6,![]() =5,则
=5,则![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() 或
或![]() D.﹣
D.﹣![]() 或﹣
或﹣![]()
7、△ABC中,已知![]() ,则A的度数等于( )
,则A的度数等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、数列![]() 中,
中,![]() =15,
=15,![]() (
(![]() ),则该数列中相邻两项的乘积是负数的是( )
),则该数列中相邻两项的乘积是负数的是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9、某厂去年的产值记为1,计划在今后五年内每年的产值比上年增长![]() ,则从今年起到第五年,这个厂的总产值为( )
,则从今年起到第五年,这个厂的总产值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D. ![]()
10、已知钝角△ABC的最长边为2,其余两边的长为![]() 、
、![]() ,则集合
,则集合![]() 所表示的平面图形面积等于( )
所表示的平面图形面积等于( )
A.2 B.![]() C.4 D.
C.4 D.![]()
11、在△ABC中,已知BC=12,A=60°,B=45°,则AC=
12.函数![]() 的定义域是
的定义域是
13.数列![]() 的前
的前![]() 项和
项和![]() ,则
,则![]()
14、设变量![]() 、
、![]() 满足约束条件
满足约束条件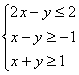 ,则
,则![]() 的最大值为
的最大值为
15、《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一。书中有一道这样的题目:把100个面包分给五人,使每人成等差数列,且使最大的三份之和的![]() 是较小的两份之和,则最小1份的大小是
是较小的两份之和,则最小1份的大小是
16、已知数列![]() 、
、![]() 都是等差数列,
都是等差数列,![]() =
=![]() ,
,![]() ,用
,用![]() 、
、![]() 分别表示数列
分别表示数列![]() 、
、![]() 的前
的前![]() 项和(
项和(![]() 是正整数),若
是正整数),若![]() +
+![]() =0,则
=0,则![]() 的值为
的值为
17、△ABC中,![]() 是A,B,C所对的边,S是该三角形的面积,且
是A,B,C所对的边,S是该三角形的面积,且![]()
(1)求∠B的大小;
(2)若![]() =4,
=4,![]() ,求
,求![]() 的值。
的值。
18、已知等差数列![]() 的前四项和为10,且
的前四项和为10,且![]() 成等比数列
成等比数列
(1)求通项公式![]()
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]()
19、已知:![]() ,当
,当![]() 时,
时,
![]() ;
;![]() 时,
时,![]()
(1)求![]() 的解析式
的解析式
(2)c为何值时,![]() 的解集为R.
的解集为R.
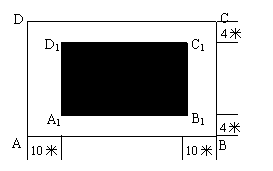
20、某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成。已知休闲区A1B1C1D1的面积为4000平方米,人行道的宽分别为4米和10米。
(1)若设休闲区的长![]() 米,求公园ABCD所占面积S关于
米,求公园ABCD所占面积S关于![]() 的函数
的函数![]() 的解析式;
的解析式;
(2)要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
 |
21、设不等式组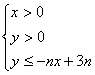 所表示的平面区域为
所表示的平面区域为![]() ,记
,记![]() 内的格点(格点即横坐标和纵坐标均为整数的点)个数为
内的格点(格点即横坐标和纵坐标均为整数的点)个数为![]()
(1)求![]() 的值及
的值及![]() 的表达式;
的表达式;
(2)记![]() ,试比较
,试比较![]() 的大小;若对于一切的正整数
的大小;若对于一切的正整数![]() ,总有
,总有![]() 成立,求实数
成立,求实数![]() 的取值范围;
的取值范围;
(3)设![]() 为数列
为数列![]() 的前
的前![]() 项的和,其中
项的和,其中![]() ,问是否存在正整数
,问是否存在正整数![]() ,使
,使![]() 成立?若存在,求出正整数
成立?若存在,求出正整数![]() ;若不存在,说明理由。
;若不存在,说明理由。
必修5参考答案
第1章 解三角形
§1.1正弦定理、余弦定理
经典例题:解:(1)∵ ![]()
![]() ∵ 2R(sin2A-sin2C)=(
∵ 2R(sin2A-sin2C)=(![]() a-b)sinB
a-b)sinB
∴ 2R[(![]() )2-(
)2-(![]() )2]=(
)2]=(![]() a-b)·
a-b)·![]() ∴ a2-c2=
∴ a2-c2=![]() ab-b2
ab-b2
∴ ![]() ∴ cosC=
∴ cosC=![]() ,∴ C=30°
,∴ C=30°
(2)∵ S=![]() absinC=
absinC=![]() ·2RsinA·2RsinB·sinC=R2sinAsinB
·2RsinA·2RsinB·sinC=R2sinAsinB
=-![]() [cos(A+B)-cos(A-B)]=
[cos(A+B)-cos(A-B)]=![]() [cos(A-B)+cosC]
[cos(A-B)+cosC]
=![]() [cos(A-B)+
[cos(A-B)+![]() ] 当cos(A-B)=1时,S有最大值
] 当cos(A-B)=1时,S有最大值![]() .,
.,
当堂练习:
1.D; 2.A; 3.D; 4.B; 5.C; 6.C; 7.B; 8.A; 9. 60°或120°; 10. 4cm和4cm; 11.50; 12. 2或;
13、解:由2sin(A+B)-=0,得sin(A+B)=, ∵△ABC为锐角三角形
∴A+B=120°, C=60°, 又∵a、b是方程x2-2x+2=0的两根,∴a+b=2,
a·b=2, ∴c2=a2+b2-2a·bcosC=(a+b)2-3ab=12-6=6,
∴c=, S△ABC=absinC=×2×= .
14.解:由=,=,可得 =,变形为sinAcosA=sinBcosB
∴sin2A=sin2B, 又∵a≠b, ∴2A=π-2B, ∴A+B=![]() . ∴△ABC为直角三角形.
. ∴△ABC为直角三角形.
由a2+b2=102和=,解得a=6, b=8, ∴内切圆的半径为r===2
15、
解:设四个角A、B、C、D的度数分别为3x、7x、4x、10x,根据四边形的内角和有3x+7x+4x+10x=360°.解得 x=15° ∴A=45°, B=105°, C=60°, D=150°
连结BD,得两个三角形△BCD和△ABD
在△BCD中,由余弦定理得
BD2=BC2+DC2-2BC·DC·cosC=a2+4a2-2a·2a·=3a2,
∴BD=a.这时DC2=BD2+BC2,可得△BCD是以DC为斜边的直角三角形.∴∠CDB=30°, 于是∠ADB=120°
在△ABD中,由正弦定理有AB= ![]() =
=![]() =
=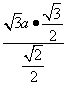 =
=![]()
∴AB的长为![]()
16、解:由tanA+tanB=tanA·tanB-可得![]() =-,即tan(A+B)=-
=-,即tan(A+B)=-
∴tan(π-C)= -, ∴-tanC=-, ∴tanC=∵C∈(0, π),
∴C=![]()
又△ABC的面积为S△ABC=,∴absinC= 即ab×=, ∴ab=6
又由余弦定理可得c2=a2+b2-2abcosC∴()2= a2+b2-2abcos![]() ∴()2= a2+b2-ab=(a+b)2-3ab
∴()2= a2+b2-ab=(a+b)2-3ab
∴(a+b)2=, ∵a+b>0, ∴a+b=
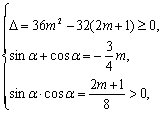 又
又![]() ,解之m=2或m=
,解之m=2或m=![]()
而2和![]() 不满足上式. 故这样的m不存在.
不满足上式. 故这样的m不存在.
§1.2正弦定理、余弦定理及其应用
1.A; 2.B; 3.D; 4.C; 5.D; 6.C; 7.B; 8.B; 9.D; 10.B; 11.C; 12.A;
13.![]() 14.
14.![]() 15.
15.![]() 16.9 17.
16.9 17.![]() 18.
18.![]()
19.468m 20.等腰三角形或直角三角形 21.a=6,b=5,c=4
22.![]() 23.
(1)
23.
(1)![]() (2)2+
(2)2+![]()
第2章 数列
§2.1数列的概念与简单表示
经典例题:解:(1)(Ⅰ)55000元(Ⅱ)63000元
(2)当n<2时(Ⅰ)方案
当n=2时(Ⅰ)(Ⅱ)方案都行
当n<2时(Ⅱ)方案
当堂练习:
1.C;
2.C; 3.D; 4.D; 5.B; 6.B; 7. 46; 8. ![]() 或
或![]() ; 9. 45; 10.
; 9. 45; 10. ![]() ;
;
11. 【 解】 (1) an=4n+5 (2) 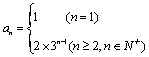
12. 【 解】 (1)1,![]() ,
, ![]() ,
,![]() ,
,![]() .(2)
.(2)![]() .
.
13. 【 解】 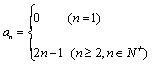
14. 【 解】 (1) ![]() (2) an +1=
(2) an +1=![]() an
(n≥1,n∈N*)(3) Sn +1=
an
(n≥1,n∈N*)(3) Sn +1=![]() Sn+
Sn+![]() (n≥1,n∈N*)
(n≥1,n∈N*)
§2.2等差数列、等比数列
经典例题:(1) (2)3 (3)5928
当堂练习:
1.B; 2.B; 3.A; 4.B; 5.B; 6.B; 7.B;8.B; 9.D; 10.B;
11. ![]() 12.
7 13.
1 14.
12.
7 13.
1 14. ![]()
15. (1) ![]() (2)
(2)![]()
16. (1) ![]() (2)
(2) 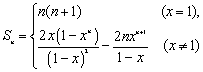
17.(1) 第2年养鸡场的个数为26个,全县出产鸡的总只数是31.2万只
(2) 到第6年这个县的养鸡业比第1年缩小了 (3) 第2年的规模最大
18.![]()
§2.3等差数列、等比数列综合运用
1.C;
2.C; 3.C; 4.B; 5.D; 6.D; 7.D; 8.D; 9.C; 10.C;11. 140,85; 12.. ![]() ; 13. 3; 14. 8
; 13. 3; 14. 8
15、(1)略;(2)![]()
16、(1)![]() ,
,![]() ;
;
(2)当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]()
17、(1)当![]() 时,
时,![]() ,由
,由![]() 得,
得,
![]() ,即
,即![]() ,又
,又![]() ,所以
,所以![]() .
.
(2)设数列![]() 的公差为
的公差为![]() ,则在
,则在![]() 中分别取
中分别取![]() 得
得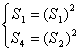
即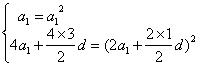 ,由(1)得
,由(1)得![]() 或
或![]() .
.
当![]() 时,代入(2)得:
时,代入(2)得:![]() 或
或![]() ;
;
当![]() 时,
时,![]() ,从而
,从而![]() 成立;
成立;
当![]() 时,则
时,则![]() ,由
,由![]() ,
,![]() 知,
知,
![]() ,故所得数列不符合题意;
,故所得数列不符合题意;
当![]() 时,
时,![]() 或
或![]() ,当
,当![]() ,
,![]() 时,
时,![]() ,从而
,从而![]()
成立;当![]() ,
, ![]() 时,则
时,则![]() ,从而
,从而![]() 成立,综上
成立,综上
共有3个满足条件的无穷等差数列;
![]() 或
或![]() 或
或![]() .
.
另解:由![]() 得
得![]() ,整理得
,整理得
![]() 对于一切正整数
对于一切正整数![]() 都
都
成立,则有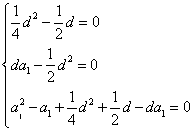 解之得:
解之得:![]() 或
或![]() 或
或![]()
所以所有满足条件的数列为:![]() 或
或![]() 或
或![]() .
.
18. (I)设甲超市第n年的年销售量为 ![]()
![]()
![]() 时
时
![]()
![]()
又 ![]() 时,
时,![]() .
. ![]()
设乙超市第n年的年销售量为![]() ,
, ![]()
![]()
![]() … …
… … ![]()
以上各式相加得: ![]()
![]()
(II)显然![]()
![]() 时
时 ![]() , 故乙超市将被早超市收购.
, 故乙超市将被早超市收购.
令 ![]() 得
得 ![]() 得
得 ![]()
![]() 时
时 ![]() 不成立. 而
不成立. 而![]() 时
时 ![]() 成立.
成立.
即
n=11时 ![]() 成立. 答:这个情况将在2011年出现,且是甲超市收购乙超市.
成立. 答:这个情况将在2011年出现,且是甲超市收购乙超市.
数列单元检测
1.D;
2.B; 3.D; 4.A; 5.B; 6.B; 7.D; 8.B; 9.B; 10.D;11.C;12.A;13. 20; 14. 7;15. ![]() ;
;
16. ![]()
![]()
![]() .
.
17. 【 解】 因![]() 的前n 项和
的前n 项和![]() ,故
,故![]() =
=![]() ,
,![]() ,
,
an=2n+a-2n-1-a=2n-1(![]() ).要使
).要使![]() 适合
适合![]() 时通项公式,则必有
时通项公式,则必有![]() ,
,
此时![]() ,
, ![]() ,
,
故当a=-1时,数列![]() 成等比数列,首项为1,公比为2,
成等比数列,首项为1,公比为2,![]() 时,
时,![]() 不是等比数列.
不是等比数列.
18. 【 解】 ∵{an}为等差数列,{bn}为等比数列,∴a2+a4=2a3,b2·b4=b32,
已知a2+a4=b3,b2·b4=a3,∴b3=2a3,a3=b32, 得b3=2b32,∵b3≠0,∴b3=![]() ,a3=
,a3=![]() .
.
由a1=1,a3=![]() ,知{an}的公差d=-
,知{an}的公差d=-![]() , ∴S10=10a1+
, ∴S10=10a1+![]() d=-
d=-![]() .
.
由b1=1,b3=![]() ,知{bn}的公比q=
,知{bn}的公比q=![]() 或q=-
或q=-![]() ,
,
![]()
19. 【 解】 (1)S3=3a1, S9=9a1, S6=6a1, 而a1≠0,所以S3,S9,S6不可能成等差数列……2分
所以q≠1,则由公式![]()
即2q6=1+q3 ∴2q6a1q=a1q+q3a1q , ∴2a8=a2+a5 所以a2, a8, a5成等差数列
(2)由2q6=1+q3=-![]()
要以a2, a8, a5为前三项的等差数列的第四项是数列{an}中的第k项,
必有ak-a5=a8-a2,所以![]() 所以
所以![]()
由k是整数,所以![]() 不可能成立,所以a2, a8, a5
为前三项的等差数列的第四项不可能也是数列{an}中的一项.
不可能成立,所以a2, a8, a5
为前三项的等差数列的第四项不可能也是数列{an}中的一项.
20. 【 解】 (Ⅰ)![]() ,
,![]() ,
, ![]()
因为![]() ,
所以
,
所以![]() 成等比数列.
成等比数列.
(Ⅱ)一般地![]() 、
、![]() 且m、n、p、r均为正整数)也成等比数列,
且m、n、p、r均为正整数)也成等比数列,![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]()
所以![]() 成等比数列.
成等比数列.
21. 【 解】 设2001年末汽车保有量为![]() 万辆,以后各年末汽车保有量依次为
万辆,以后各年末汽车保有量依次为![]() 万辆,
万辆,![]() 万辆,……,每年新增汽车
万辆,……,每年新增汽车![]() 万辆,则
万辆,则 ![]() ,
,![]()
所以,当![]() 时,
时,![]() ,两式相减得:
,两式相减得:![]()
(1)显然,若![]() ,则
,则![]() ,即
,即![]() ,此时
,此时![]() (2)若
(2)若![]() ,则数列
,则数列![]() 为以
为以![]() 为首项,以
为首项,以![]() 为公比的等比数列,所以,
为公比的等比数列,所以,![]() .
.
(i)若![]() ,则对于任意正整数
,则对于任意正整数![]() ,均有
,均有![]() ,所以,
,所以,![]() ,此时,
,此时,![]()
(ii)当![]() 时,
时,![]() ,则对于任意正整数
,则对于任意正整数![]() ,均有
,均有![]() ,所以,
,所以,![]() ,由
,由![]() ,得
,得
![]()
![]() ,
,
要使对于任意正整数![]() ,均有
,均有![]() 恒成立, 即
恒成立, 即 ![]()
对于任意正整数![]() 恒成立,解这个关于x的一元一次不等式 , 得
恒成立,解这个关于x的一元一次不等式 , 得 ![]() ,
,
上式恒成立的条件为:![]() ,由于关于
,由于关于![]() 的函数
的函数![]() 单调递减,所以,
单调递减,所以,![]() .
.
第3章 不等式
§3.1不等关系、一元二次不等式
经典例题:79.94km/h
当堂练习:
1.D;
2.C; 3.C; 4.A; 5.C; 6.D; 7.A;8.C; 9.A; 10.D;11. (-8,8); 12.![]() ;
;
13. ![]() ; 14. 18;
; 14. 18;
15. ![]() ;
;
16. ![]() ; 17.半圆直径与矩形的高的比为2∶1 ; 18.
; 17.半圆直径与矩形的高的比为2∶1 ; 18.![]() .
.
§3.3二元一次不等式组与简单的线性规划问题
经典例题:79.94km/h
当堂练习:
1.D;
2.C; 3.C; 4.A; 5.C; 6.D; 7.A;8.C; 9.A; 10.D;11. (-8,8); 12.![]() ;
;
13. ![]() ; 14. 18;
; 14. 18;
15. ![]() ;
;
16. ![]() ; 17.半圆直径与矩形的高的比为2∶1 ; 18.
; 17.半圆直径与矩形的高的比为2∶1 ; 18.![]() .
.
§3.3二元一次不等式组与简单的线性规划问题
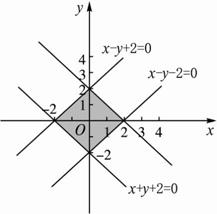
经典例题:思路分析:主要是去绝对值,可以运用分类讨论思想依绝对值的定义去掉绝对值符号.也可以运用化归、转化思想化陌生问题为熟悉问题,化复杂问题为简单问题.
解法一:原不等式x-2+y-2≤2等价于
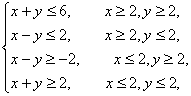 作出以上不等式组所表示的平面区域:它是边长为22的正方形,其面积为8.
作出以上不等式组所表示的平面区域:它是边长为22的正方形,其面积为8.
解法二:∵x-2+y-2≤2是x+y≤2经过向右、向上各平移2个单位得到的,
∴x-2+y-2≤2表示的平面区域的面积等于x+y≤2表示的平面区域的面积,由于x+y≤2的图象关于x轴、y轴、原点均对称,故求得平面区域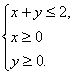 如下图所示的面积为2,故x+y≤2的面积为4×2=8.
如下图所示的面积为2,故x+y≤2的面积为4×2=8.
∴所求面积为8.
当堂练习:
1.C;
2.B; 3. 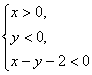 ; 4. 甲地运往B地300t,乙地运往A地200t,运往B地150t,运往C地400t,5650元;
; 4. 甲地运往B地300t,乙地运往A地200t,运往B地150t,运往C地400t,5650元;
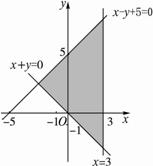 5. 思路分析:不等式组表示的平面区域是各个不等式所表示的平面点集的交集,因而是各个不等式所表示的平面区域的公共部分.
5. 思路分析:不等式组表示的平面区域是各个不等式所表示的平面点集的交集,因而是各个不等式所表示的平面区域的公共部分.
解:运用“直线定界,特殊点定域”的方法,先画出
直线x-y+5=0(画成实线),如下图,取原点(0,0),
代入x-y+5.∵0-0+5=5>0,∴原点在x-y表示的
平面区域内,即x-y+5≥0表示直线x-y+5=0上及右
下方的点的集合,同理可得x+y≥0表示直线x+y=0
上及右上方的点的集合,x≤3表示直线x=3上及左方的点的集合.
6. 思路分析:这是一个求最大利润问题,首先根据条件设种两种作物分别为x、y亩,根据条件列出不等式组和目标函数画图,即可得到最大利润.
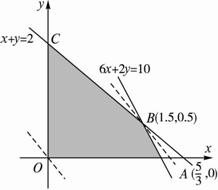 解:如下图所示,设水稻种x亩,花生种y亩,则由题意得
解:如下图所示,设水稻种x亩,花生种y亩,则由题意得
而利润P=(3×400-240)x+(5×100-80)y
=960x+420y(目标函数),
可联立![]() 得交点B(1.5,0.5).
得交点B(1.5,0.5).
故当x=1.5,y=0.5时,
Pmax=960×1.5+420×0.5=1650,
即水稻种1.5亩,花生种0.5亩时所得到的利润最大.
7. 思路分析:可以把a、b分别看成横坐标和纵坐标,根据不等式组画出可行域,然后求目标函数9x-y的最大值和最小值.
解:问题转化为在约束条件![]() 下,目标函数z=9a-b的取值范围.
下,目标函数z=9a-b的取值范围.
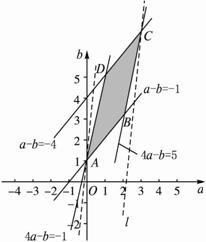 画出可行域如下图所示的四边形ABCD及其内部.
画出可行域如下图所示的四边形ABCD及其内部.
由![]() ,解得
,解得![]() 得点A(0,1).
得点A(0,1).
当直线9a-b=t通过与可行域的公共点A(0,1)时,
使目标函数z=9a-b取得最小值为zmin=9×0-1=-1.
由![]() 解得
解得![]() 得点C(3,7).
得点C(3,7).
当直线9a-b=t通过与可行域的公共点C(3,7)时,
使目标函数z=9a-b取得最大值为zmax=9×3-7=20.
∴9a-b的取值范围是[-1,20].
8. 思路分析:本题考查逆向思维、数形结合的思想方法,利用图形的特性和规律,解决数的问题或将图形信息转换成代数信息,削弱或清除形的推理部分,使要解决的形问题转化为数量关系的讨论.
解:直线z=ax+y(a>0)是斜率为-a,y轴上的截距为z的直线族,从题图可以看出,当-a小于直线AC的斜率时,目标函数z=ax+y(a>0)取得最大值的最优解是(1,4);当-a大于直线AC的斜率时,目标函数z=ax+y(a>0)取得最大值的最优解是(5,2);
只有当-a等于直线AC的斜率时,目标函数z=ax+y(a>0)取得最大值的最优解有无穷多个,线段AC上的所有点都是最优解.直线AC的斜率为-![]() ,所以a=
,所以a=![]() 时,z的最大值为
时,z的最大值为![]() ×1+4=
×1+4=![]() .
.
9. 思路分析:本题可以使用线性规划的基本思路,像二元一次不等式所示的区域一样,我们仍然可以用“线定界,点定域”的方法来确定9x2-16y2+144≤0所表示的平面区域.
解:(1)将原点坐标代入9x2-16y2+144,其值为144>0,因此9x2-16y2+144≤0表示的平面区域如图所示的阴影部分,即双曲线![]() -
-![]() =1的含有焦点的区域.
=1的含有焦点的区域.
(2)设P(x,y)为该区域内任意一点,由上图可知,当P与双曲线的顶点(0,±4)重合时,OP取得最小值4.所以,x2+y2=OP2=16.
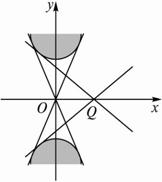 (3)取Q(2,0),则直线PQ的斜率为k=
(3)取Q(2,0),则直线PQ的斜率为k=![]() ,其直线方程为y=k(x-2),代入9x2-16y2+144=0得(9-16k2)x2+64k2x-64k2+144=0,由Δ=0得k=±
,其直线方程为y=k(x-2),代入9x2-16y2+144=0得(9-16k2)x2+64k2x-64k2+144=0,由Δ=0得k=±![]() ,
,
由图可知k≥![]() 或k≤-
或k≤-![]() .
.
故所求![]() 的取值范围是(-∞,-
的取值范围是(-∞,- ![]() ]∪[
]∪[![]() ,+∞).
,+∞).
§3.4基本不等式
经典例题:
【 解析】 证法一 假设![]() ,
,![]() ,
,![]() 同时大于
同时大于![]() ,
,
∵ 1-a>0,b>0,∴ ![]() ≥
≥![]() ,
,
同理![]() ,
,![]() .三个不等式相加得
.三个不等式相加得![]() ,不可能,
,不可能,
∴ (1-a)b,(1-b)c,(1-c)a不可能同时大于![]() .
.
证法二 假设![]() ,
,![]() ,
,![]() 同时成立,
同时成立,
∵ 1-a>0,1-b>0,1-c>0,a>0,b>0,c>0,∴ ![]() ,
,
即![]() . (*) 又∵
. (*) 又∵ ![]() ≤
≤![]() ,
,
同理![]() ≤
≤![]() ,
,![]() ≤
≤![]() ,
,
∴![]() ≤
≤![]() 与(*)式矛盾,
与(*)式矛盾,
故![]() 不可能同时大于
不可能同时大于![]() .
.
当堂练习:
1.A;
2.B; 3.C; 4.D; 5.C; 6.A; 7.B; 8.C; 9.C; 10.C;11. ![]() ;
12. 3600 ;
;
12. 3600 ;
13. ![]() ; 14. 对;
; 14. 对;
15.![]()
16. 【 解析】 ![]()
![]() .
.
∵ ![]() 、
、![]() , ∴
, ∴ ![]() .
.
当且仅当![]() =
=![]() 时,取“=”号.
时,取“=”号.
当![]() 时,有
时,有![]() .
.
∴ ![]()
![]()
![]() .
.![]() .
.
即![]() .
.
当![]() 时,有
时,有![]()
![]() .
.
即![]()
17. (1)![]() (2)
(2)![]()
18.【 解析】 证明 由于不等式![]()
对所有的正整数k成立,把它对k从1到n(n≥1)求和,得到
![]()
又因 ![]() 以及
以及![]()
因此不等式![]() 对所有的正整数n都成立.
对所有的正整数n都成立.
§3.5不等式单元测试
1.C;
2.A; 3.D; 4.C; 5.C; 6.D; 7.A; 8.D; 9.B; 10.A;11. ![]() ; 12.
; 12.![]() ; 13. 20 ; 14.
; 13. 20 ; 14. ![]() ;15.
;15.![]() ;
;
16.解:原不等式等价于:
![]()
![]() 或
或![]()
∴原不等式的解集为![]()
17.解:不等式![]() 可化为
可化为![]() .
.
∵![]() ,∴
,∴![]() ,则原不等式可化为
,则原不等式可化为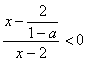 ,
,
故当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;
;
当![]() 时,原不等式的解集为
时,原不等式的解集为![]() ;
;
当![]() 时,原不等式的解集为
时,原不等式的解集为![]() .
.
18.证明:法一(综合法)
![]() ,
,
![]()
展开并移项得:![]()
![]()
法二(分析法)
要证![]() ,
,![]() ,故只要证
,故只要证![]()
即证![]() ,
,
也就是证![]() ,
,
而此式显然成立,由于以上相应各步均可逆,∴原不等式成立。
法三:![]() ,
,![]()
![]()
![]()
法四:![]()
![]() ,
,![]()
∴由三式相加得:![]()
两边同时加上![]() 得:
得:![]()
![]() ,
∴
,
∴![]()
19.解:设![]() ,
,
则![]() 的图象为一直线,在
的图象为一直线,在![]() 上恒大于0,故有
上恒大于0,故有
![]() ,即
,即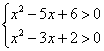 ,解得:
,解得:![]() 或
或![]()
∴![]() 的取值范围是
的取值范围是![]()
20.解:设花坛的长、宽分别为xm,ym,根据要求,矩形花坛应在喷水区域内,顶点应恰好位于喷水区域的边界。依题意得:![]() ,(
,(![]() )
)
问题转化为在![]() ,
,![]() 的条件下,求
的条件下,求![]() 的最大值。
的最大值。
法一:![]() ,
,
由![]() 和
和![]() 及
及![]() 得:
得:![]()
![]()
法二:∵![]() ,
,![]() ,
,
![]() =
=![]()
∴当![]() ,即
,即![]() ,
,![]()
由![]() 可解得:
可解得:![]() 。
。
答:花坛的长为![]() ,宽为
,宽为![]() ,两喷水器位于矩形分成的两个正方形的中心,则符合要求。
,两喷水器位于矩形分成的两个正方形的中心,则符合要求。
21. 解:(1)对任意的![]() ,都有
,都有![]()
对任意的![]() ,
,![]()
![]()
![]() ∴
∴![]() .
.
(2)证明:∵![]()
![]() ∴
∴![]() ,即
,即![]() 。
。
(3)证明:由![]() 得,
得,![]() ∴
∴![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数。
上是增函数。
∴当![]() 时,
时,![]() 在
在![]() 时取得最小值
时取得最小值![]() ,在
,在![]() 时取得最大值
时取得最大值![]() .
.
故对任意的![]() ,
,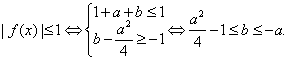
![]()
必修5综合测试
1.D;
2.B; 3.B; 4.B; 5.C; 6.C; 7.A; 8.C; 9.D; 10.B;11. ![]() ; 12.
; 12.![]() ; 13. 48 ; 14.18;
15.10; 16.5;
; 13. 48 ; 14.18;
15.10; 16.5;
17、⑴由![]()
![]()
![]()
![]()
![]()
⑵![]()
![]()
18、⑴由题意知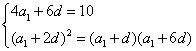
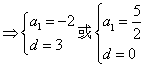
所以![]()
⑵当![]() 时,数列
时,数列![]() 是首项为
是首项为![]() 、公比为8的等比数列
、公比为8的等比数列
所以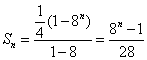
当![]() 时,
时,![]() 所以
所以![]()
综上,所以![]() 或
或![]()
19、⑴由![]() 时,
时,![]() ;
;![]() 时,
时,![]()
知:![]() 是是方程
是是方程![]() 的两根
的两根
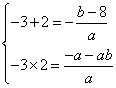
![]()
![]()
⑵由![]() ,知二次函数
,知二次函数![]() 的图象开口向下
的图象开口向下
要使![]() 的解集为R,只需
的解集为R,只需![]()
即![]()
∴当![]() 时
时![]() 的解集为R.
的解集为R.
20、⑴由![]() ,知
,知![]()
![]()
![]()
⑵![]()
当且仅当![]() 时取等号
时取等号
∴要使公园所占面积最小,休闲区A1B1C1D1的长为100米、宽为40米.
21、⑴![]()
当![]() 时,
时,![]() 取值为1,2,3,…,
取值为1,2,3,…,![]() 共有
共有![]() 个格点
个格点
当![]() 时,
时,![]() 取值为1,2,3,…,
取值为1,2,3,…,![]() 共有
共有![]() 个格点
个格点
∴![]()
⑵![]()
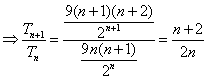
当![]() 时,
时,![]()
当![]() 时,
时,![]()
∴![]() 时,
时,![]()
![]() 时,
时,![]()
![]() 时,
时,![]()
∴![]() 中的最大值为
中的最大值为![]()
要使![]() 对于一切的正整数
对于一切的正整数![]() 恒成立,只需
恒成立,只需![]() ∴
∴![]()
⑶![]()
将![]() 代入
代入![]() ,化简得,
,化简得,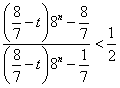 (﹡)
(﹡)
若![]() 时
时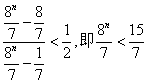 ,显然
,显然![]()
若![]() 时
时![]() (﹡)式化简为
(﹡)式化简为![]() 不可能成立
不可能成立
综上,存在正整数![]() 使
使![]() 成立.
成立.