![]() 选修1-1
第1章 常用逻辑用语
选修1-1
第1章 常用逻辑用语
§1.1命题及其关系
重难点:了解命题及其逆命题、否命题与逆否命题;明白四种命题之间的关系;会利用两个命题互为逆否命题的关系判别命题的真假.
考纲要求:①了解命题及其逆命题、否命题与逆否命题.
②理解必要条件、充分条件与充要条件的意义,会分析四种命题的互相关系.
经典例题:已知命题![]() ;
;![]() 若
若![]() 是
是![]() 的充分非必要条件,试求实数
的充分非必要条件,试求实数![]() 的取值范围.
的取值范围.
当堂练习:
1. 给出以下四个命题:
①“若x+y=0,则x,y互为相反数”的逆命题;②“全等三角形的面积相等”的否命题;
③“若![]() ,则
,则![]() 有实根”的逆否命题;
有实根”的逆否命题;
④“不等边三角形的三内角相等”的逆否命题.
其中真命题是 ( )
A.①② B.②③
C.①③ D.③④
1. “△ABC中,若∠C=90°,则∠A、∠B都是锐角”的否命题为 ( )
A.△ABC中,若∠C≠90°,则∠A、∠B都不是锐角
B.△ABC中,若∠C≠90°,则∠A、∠B不都是锐角
C.△ABC中,若∠C≠90°,则∠A、∠B都不一定是锐角
D.以上都不对
3. 给出4个命题:
①若![]() ,则x=1或x=2;
,则x=1或x=2;
②若![]() ,则
,则![]() ;
;
③若x=y=0,则![]() ;
;
④若![]() ,x+y是奇数,则x,y中一个是奇数,一个是偶数.
,x+y是奇数,则x,y中一个是奇数,一个是偶数.
那么: ( )
A.①的逆命题为真 B.②的否命题为真
C.③的逆否命题为假 D.④的逆命题为假
4. 命题“若△ABC不是等腰三角形,则它的任何两个内角不相等.”的逆否命题是 ( )
A.“若△ABC是等腰三角形,则它的任何两个内角相等.”
B.“若△ABC任何两个内角不相等,则它不是等腰三角形.”
C.“若△ABC有两个内角相等,则它是等腰三角形.”
D.“若△ABC任何两个角相等,则它是等腰三角形.”
5. 命题p:若A∩B=B,则![]() ;命题q:若
;命题q:若![]() ,则A∩B≠B.那么命题p与命题q的关系是( )
,则A∩B≠B.那么命题p与命题q的关系是( )
A.互逆 B.互否
C.互为逆否命题 D.不能确定
6. 对以下四个命题的判断正确的是 ( )
(1)原命题:若一个自然数的末位数字为0,则这个自然数能被5整除
(2)逆命题:若一个自然数能被5整除,则这个自然数的末位数字为0
(3)否命题:若一个自然数的末位数字不为0,则这个自然数不能被5整除
(4)逆否命题:若一个自然数不能被5整除,则这个自然数的末位数字不为0
A.(1)、(3)为真,(2)、(4)为假 B.(1)、(2)为真,(3)、(4)为假
C.(1)、(4)为真,(2)、(3)为假 D.(2)、(3)为真,(1)、(4)为假
7. 直线![]() 的倾斜角为钝角的一个必要非充分条件是
( )
的倾斜角为钝角的一个必要非充分条件是
( )
A.k<0 B.k<-1 C.k<1 D.k>-2
8. 直线![]() ,
,![]() 互相平行的一个充分条件是 ( )
互相平行的一个充分条件是 ( )
A. ![]() ,
,![]() 都平行于同一个平面 B.
都平行于同一个平面 B. ![]() ,
,![]() 与同一个平面所成的角相等
与同一个平面所成的角相等
C. ![]() 平行于
平行于![]() 所在的平面
D.
所在的平面
D. ![]() ,
,![]() 都垂直于同一个平面
都垂直于同一个平面
9. 已知a1,a2,a3,a4是非零实数,则a1a4=a2a3是a1,a2,a3,a4成等比数列的( )
A.充分非必要条件 B.必要非充分条件
C.充分且必要条件 D.既不充分又不必要条件
10. 在ΔABC中,条件甲:A<B,条件乙:cos![]() A> cos
A> cos![]() B,则甲是乙的 ( )
B,则甲是乙的 ( )
A.充分非必要条件 B.必要非充分条件
C.充要条件 D.既非充分又非必要条件
11. 在空间中,①若四点不共面,则这四点中任何三点都不共线;②若两条直线没有公共点,则这两条直线是异面直线.以上两个命题中,逆命题为真命题的是 (把符合要求的命题序号都填上).
12.命题![]() 则对复合命题的下述判断:①p或q为真;②p或
则对复合命题的下述判断:①p或q为真;②p或
q为假;③p且q为真;④p且q为假;⑤非p为真;⑥非q为假.其中判断正确的序号是 (填上你认为正确的所有序号).
13. 设集合A={xx2+x-6=0}, B={xmx+1=0},则B是A的真子集的一个充分不必要的条件是_ .
14. 设甲是乙的充分不必要条件,乙是丙的充要条件,丁是丙的必要不充分条件,那么甲是丁的__________条件.
15. 写出下列命题的逆命题、否命题、逆否命题,并指出他们的真假:
(1)若xy=0,则x,y中至少有一个是0;
(2)若x>0,y>0,则xy>0;
16. 设集合![]() ,
,![]() ,则“
,则“![]() 或
或![]() ”是“
”是“![]() ”的什么条件?
”的什么条件?
17. 已知关于x的一元二次方程 (m∈Z)
① mx2-4x+4=0 ② x2-4mx+4m2-4m-5=0求方程①和②都有整数解的充要条件
18.设α,β是方程x2-ax+b=0的两个实根,试分析a>2且b>1是两根α、β均大于1的什么条件?
![]() 选修1-1
第1章 常用逻辑用语
选修1-1
第1章 常用逻辑用语
§1.2简单的逻辑联结词
重难点:通过实例,了解逻辑联结词“或”、“且”、“非”的含义;能准确区分命题的否定与否命题.
考纲要求:①了解逻辑联结词“或”、“且”、“非”的含义.
经典例题:已知p:方程x2+mx+1=0有两个不等的负根;q:方程4x2+4(m-2)x+1=0无实根.若“p或q”为真,“p且q”为假,求m的取值范围.
当堂练习:
1. 下列命题中为简单命题的是 ( )
A.8或6是30的约数 B.菱形的对角线垂直平分
C.![]() 是无理数
D.方程
是无理数
D.方程![]() 没有实数根
没有实数根
2. 有下列命题:
①面积相等的三角形是全等三角形;
②“若xy=0,则![]() ”的逆命题;
”的逆命题;
③“若a>b,则a+c>b+c ”的否命题;
④“矩形的对角线互相垂直”的逆否命题.
其中真命题共有 ( )
A.1个 B.2个
C.3个 D.4个
3. 已知命题p:若实数x、y满足![]() 则x、y全为0;命题q:若
则x、y全为0;命题q:若![]() 给出下列四个复合命题:①p且q,②p或q,③
给出下列四个复合命题:①p且q,②p或q,③
![]() p,④
p,④
![]() q.其中真命题的个数为(
)
q.其中真命题的个数为(
)
A.1 B.2
C.3 D.4
4. 在原命题及其逆命题、否命题、逆否命题这四个命题中,真命题的个数可以是( )
A.1或2或3或4 B.0或2或4
C.1或3 D.0或4
5. 若命题p:2n-1是奇数,q:2n+1是偶数,则下列说法中正确的是( )
A.p或q为真 B.p且q为真
C. 非p为真 D. 非p为假
6. “至多三个”的否定为 ( )
A.至少有三个 B.至少有四个 C. 有三个 D. 有四个
7. “![]() ”的含义是
( )
”的含义是
( )
A.![]() 不全为0 B.
不全为0 B.![]() 全不为0
全不为0
C.![]() 至少有一个为0
D.
至少有一个为0
D.![]() 不为0且
不为0且![]() 为0,或
为0,或![]() 不为0且
不为0且![]() 为0
为0
8. 如果命题“非p”与命题“p或q”都是真命题,那么 ( )
A.命题p与命题q的真值相同 B.命题q一定是真命题
C.命题q不一定是真命题 D.命题p不一定是真命题
9. 如果命题“非p”与命题“p或q”都是真命题,那么 ( )
A.命题p与命题q的真值相同 B.命题q一定是真命题
C.命题q不一定是真命题 D.命题p不一定是真命题
10. 由下列各组命题构成“p或q”为真,“p且q”为假,非“p”为真的是 ( )
A.![]()
![]() ,
,![]() Æ B.p:等腰三角形一定是锐角三角形,q:正三角形都相似
Æ B.p:等腰三角形一定是锐角三角形,q:正三角形都相似
C.![]()
![]()
![]() ,
,![]() D.
D.![]() 12是质数
12是质数
11. 命题A:底面为正三角形,且顶点在底面的射影为底面中心的三棱锥是正三棱锥;命题A的等价命题B可以是:底面为正三角形,且______________的三棱锥是正三棱锥.
12. 由命题p:6是12的约数,q:6是24的约数,构成的“p或q”形式的命题是:_ ___,“p且q”形式的命题是__ _,“非p”形式的命题是__ _.
13. 在空间中,①若四点不共面,则这四点中任何三点都不共线;②若两条直线没有公共点,则这两条直线是异面直线.以上两个命题中,逆命题为真命题的是 (把符合要求的命题序号都填上).
14. 所给命题:
①菱形的两条对角线互相平分的逆命题;
②![]() =
= ![]()
![]()
![]() ;
;
③对于命题:“p且q”,若p假q真,则“p且q”为假;
④有两条边相等且有一个内角为60°是一个三角形为等边三角形的充要条件.
其中为真命题的序号为 .
15. 写出下列各组命题的“或”命题,并判断其真假
①p:2=2;q:2>2.
②p:正方形的对角线互相垂直;q:矩形的对角线互相平分.
16. 关于x的不等式![]() 与指数函数
与指数函数![]() 若命题“p的解集为
若命题“p的解集为![]() 或
或![]() 在
在![]() 内是增函数”是真命题,求实数
内是增函数”是真命题,求实数![]() 的取值范围.
的取值范围.
17. 若三条抛物线![]() 中至少有一条与x轴有公共点,求a的取值范围.
中至少有一条与x轴有公共点,求a的取值范围.
18. 已知命题p:x2-x|≥6,q:x∈Z,且“p且q”与“非q”同时为假命题,求x的值.
![]() 选修1-1
第1章 常用逻辑用语
选修1-1
第1章 常用逻辑用语
§1.3全称量词与存在量词
重难点:通过生活和数学中丰富实例,理解全称量词与存在量词的意义地利用;能准确全称量词与存在量词的意义.
考纲要求:①理解全称量词与存在量词的意义.
②能正确地对含有一个量词的命题进行否定.
经典例题:判断下列命题是全称命题还是存在性命题.
(1)线段的垂直平分线上的点到这条线段两个端点的距离相等; (2)负数的平方是正数;
(3)有些三角形不是等腰三角形; (4)有些菱形是正方形.
当堂练习:
1. 对于命题“任何实数的平方都是非负的”,下列叙述正确的是 ( )
A.是全称命题 B.是存在性命题
C.是假命题 D.是“若p则q”形式的命题
2. 命题“原函数与反函数的图象关于y=x对称”的否定是( )
A 原函数与反函数的图象关于y=-x对称
B 原函数不与反函数的图象关于y=x对称
C 存在一个原函数与反函数的图象不关于y=x对称
D 存在原函数与反函数的图象关于y=x对称
3. 下列全称命题中,真命题是 ( )
A.所有的素数是奇数
B. ![]() , (x-1)2>0
, (x-1)2>0
C.![]() , x+≥2
D.
, x+≥2
D. ![]() , sinx+≥2
, sinx+≥2
4. 下列存在性命题中,假命题是 ( )
A. ![]() ,
, ![]() B.至少有一个x∈Z.x能被2和3整除
B.至少有一个x∈Z.x能被2和3整除
C.存在两个相交平面垂直于同一个直线
D. ![]() 是无理数}.x2是有理数
是无理数}.x2是有理数
5. 下列全称命题中假命题的个数是( )
① 2x+1是整数(x∈R)②对所有的x∈R ,x>3③对任意一个x∈z,2x2+1为奇数
A 0 B 1 C 2 D 3
6.下列全称命题中真命题的个数是( )
① 末位是0的整数,可以被2整除②角平分线上的点到这个角的两边的距离相等
③正四面体中两侧面的夹角相等
A 1 B 2 C 3 D 4
7.下列存在性命题中假命题的个数是( )
① 有的实数是无限不循环小数②有些三角形不是等腰三角形③有的菱形是正方形
A 0 B 1 C 2 D 3
8.下列特称命题中真命题的个数是( )
①![]() ②至少有一个整数,它既不是合数,也不是素数
②至少有一个整数,它既不是合数,也不是素数
③![]()
A 0 B 1 C 2 D 3
9.下列命题为存在性命题的是( )
A 偶函数的图象关于y轴对称 B 正四棱柱都是平行六面体
C 不相交的两条直线是平行直线 D 存在实数大于等于3
10.下列全称命题中真命题的个数是( )
① 末位是0的整数,可以被2整除②角平分线上的点到这个角的两边的距离相等
③正四面体中两侧面的夹角相等
A 1 B 2 C 3 D 4
11.命题“任何有理数的平方仍是有理数”用数学符号语言可以表示为 .
12.命题“存在实数是有理数”用数学符号语言可以表示为 .
13.命题“存在实数是有理数”的否定用数学符号语言可以表示为 .
14.命题“存在一个三角形没有外接圆”的否定是___________________.
15.判断下列命题的真假:
(1) ![]() .+1≥x;
.+1≥x;
(2) ![]() .+1≥x;
.+1≥x;
(3)存在无穷多个既是奇函数又是偶函数的函数;
(4)有些相似三角形是全等三角形.
16. 判断下列命题是全称命题还是存在性命题,并判断真假:
(1)正方形对角线互相垂直平分:
(2)所有中国人都讲汉语;
(3)有些数比它的平方大;
(4)有些实数的平方根是无理数.
17. 已知:对![]() ,a< x+恒成立,求a的取值范围
.
,a< x+恒成立,求a的取值范围
.
18.写出下列命题的否定.
(1) 对所有的正数x, >x-1 ;
(2) 不存在实数x,x2+1<2x”;
(3) 集合A中的任意一个元素都是集合B的元素;
(4) 集合A中至少有一个元素是集合B的元素.
![]() 选修1-1
第1章 常用逻辑用语
选修1-1
第1章 常用逻辑用语
§1.4常用逻辑用语单元测试
1.函数f(x)=xx+a+b是奇函数的充要条件是 ( )
A.ab=0 B.a+b=0 C.a=b D.a2+b2=0
2.“至多有三个”的否定为 ( )
A.至少有三个 B.至少有四个 C.有三个 D.有四个
3.有金盒、银盒、铅盒各一个,只有一个盒子里有肖像.金盒上写有命题p:肖像在这个盒子里;银盒上写有命题q:肖像不在这个盒子里;铅盒上写有命题r:肖像不在金盒里.p、q、r中有且只有一个是真命题,则肖像在 ( )
A.金盒里 B.银盒里
C.铅盒里 D.在哪个盒子里不能确定
4.不等式![]() 对于
对于![]() 恒成立,那么
恒成立,那么![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.“a和b都不是偶数”的否定形式是 ( )
A.a和b至少有一个是偶数 B.a和b至多有一个是偶数
C.a是偶数,b不是偶数 D.a和b都是偶数
6.某食品的广告词为:“幸福的人们都拥有”,初听起来,这似乎只是普通的赞美说词,然
而他的实际效果大哩,原来这句话的等价命题是 ( )
A.不拥有的人们不一定幸福 B.不拥有的人们可能幸福
C.拥有的人们不一定幸福 D.不拥有的人们不幸福
7.若命题“p或q”为真,“非p”为真,则 ( )
A.p真q真 B.p假q真 C.p真q假 D.p假q假
8.条件p:![]() ,
,![]() ,条件q:
,条件q:![]() ,
,![]() ,则条件p是条件q的(
)
,则条件p是条件q的(
)
A.充分而不必要条件 B.必要而不充分条件
C.充要条件 D.即不充分也不必要条件
9.2x2-5x-3<0的一个必要不充分条件是 ( )
A.-![]() <x<3 B.-
<x<3 B.-![]() <x<0 C.-3<x<
<x<0 C.-3<x<![]() D.-1<x<6
D.-1<x<6
10.设原命题:若a+b≥2,则a,b 中至少有一个不小于1。则原命题与其逆命题的真假情况是( )
A.原命题真,逆命题假 B.原命题假,逆命题真
C.原命题与逆命题均为真命题 D.原命题与逆命题均为假命题
11.下列命题中_________为真命题.
①“A∩B=A”成立的必要条件是“A![]() B”;
B”;
②“若x2+y2=0,则x,y全为0”的否命题;
③“全等三角形是相似三角形”的逆命题;
④“圆内接四边形对角互补”的逆否命题。
12.若p:“平行四边形一定是菱形”,则“非p”为___ _____。
13.已知p,q都是r的必要条件,s是r的充分条件,q是s的充分条件,则s是q的 条件,r是q的 条件,p是s的 条件。
14.设p、q是两个命题,若p是q的充分不必要条件,那么非p是非q的 条件。
15.分别写出下列命题的逆命题,否命题,逆否命题,并判断其真假。
(1)矩形的对角线相等且互相平分;
(2)正偶数不是质数。
16.写出由下述各命题构成的“p或q”,“p且q”,“非p”形式的复合命题,并指出所构成的这些复合命题的真假.
(1)p:连续的三个整数的乘积能被2整除,q:连续的三个整数的乘积能被3整除。
(2)p:对角线互相垂直的四边形是菱形,q:对角线互相平分的四边形是菱形。
17.给定两个命题,
![]() :对任意实数
:对任意实数![]() 都有
都有![]() 恒成立;
恒成立;![]() :关于
:关于![]() 的方程
的方程![]() 有实数根;如果
有实数根;如果![]() 与
与![]() 中有且仅有一个为真命题,求实数
中有且仅有一个为真命题,求实数![]() 的取值范围。
的取值范围。
18.已知p,q都是r的必要条件,s是r的充分条件,q是s的充分条件,那么
(1)s是q的什么条件?(2)r是q的什么条件?(3)p是q的什么条件?
19.设0<a, b,
c<1,求证:(1-a)b,(1-b)c,(1-c)a不同时大于![]() .
.
20.求证:关于x的方程x2+2ax+b=0 有实数根,且两根均小于2的充分但不必要条件是a≥2且b ≤4.
![]() 选修1-1
第2章 圆锥曲线与方程
选修1-1
第2章 圆锥曲线与方程
考纲总要求:①了解圆锥曲线的实际背景,了解在刻画现实世界和解决实际问题中的作用.
②掌握椭圆的定义、几何图形、标准方程及简单几何性质.
③了解双曲线、抛物线的定义、几何图形和标准方程,知道它们的简单几何性质.
④理解数形结合的思想.
⑤了解圆锥曲线的简单应用.
§2.1-2椭圆
重难点:建立并掌握椭圆的标准方程,能根据已知条件求椭圆的标准方程;掌握椭圆的简单几何性质,能运用椭圆的几何性质处理一些简单的实际问题.
经典例题:已知A、B为椭圆![]() +
+![]() =1上两点,F2为椭圆的右焦点,若AF2+BF2=
=1上两点,F2为椭圆的右焦点,若AF2+BF2=![]() a,AB中点到椭圆左准线的距离为
a,AB中点到椭圆左准线的距离为![]() ,求该椭圆方程.
,求该椭圆方程.
当堂练习:
1.下列命题是真命题的是 ( )
A.到两定点距离之和为常数的点的轨迹是椭圆
B.到定直线![]() 和定点F(c,0)的距离之比为
和定点F(c,0)的距离之比为![]() 的点的轨迹是椭圆
的点的轨迹是椭圆
C.到定点F(-c,0)和定直线![]() 的距离之比为
的距离之比为![]() (a>c>0)的点的轨迹 是左半个椭圆
(a>c>0)的点的轨迹 是左半个椭圆
D.到定直线![]() 和定点F(c,0)的距离之比为
和定点F(c,0)的距离之比为![]() (a>c>0)的点的轨迹是椭圆
(a>c>0)的点的轨迹是椭圆
2.若椭圆的两焦点为(-2,0)和(2,0),且椭圆过点![]() ,则椭圆方程是 ( )
,则椭圆方程是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.若方程x2+ky2=2表示焦点在y轴上的椭圆,则实数k的取值范围为 ( )
A.(0,+∞) B.(0,2) C.(1,+∞) D.(0,1)
4.设定点F1(0,-3)、F2(0,3),动点P满足条件![]() ,则点P的轨迹是( )
,则点P的轨迹是( )
A.椭圆 B.线段 C.不存在 D.椭圆或线段
5.椭圆![]() 和
和![]()
![]() 具有 ( )
具有 ( )
A.相同的离心率 B.相同的焦点 C.相同的顶点 D.相同的长、短轴
6.若椭圆两准线间的距离等于焦距的4倍,则这个椭圆的离心率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.
![]()
7.已知![]() 是椭圆
是椭圆![]() 上的一点,若
上的一点,若![]() 到椭圆右准线的距离是
到椭圆右准线的距离是![]() ,则点
,则点![]() 到左焦点的距离( )
到左焦点的距离( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.椭圆![]() 上的点到直线
上的点到直线![]() 的最大距离是 ( )
的最大距离是 ( )
A.3 B.![]() C.
C.![]() D.
D.![]()
9.在椭圆![]() 内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使MP+2MF的值最小,则这一最小值是 ( )
内有一点P(1,-1),F为椭圆右焦点,在椭圆上有一点M,使MP+2MF的值最小,则这一最小值是 ( )
A.![]() B.
B.![]() C.3 D.4
C.3 D.4
10.过点M(-2,0)的直线m与椭圆![]() 交于P1,P2,线段P1P2的中点为P,设直线m的斜率为k1(
交于P1,P2,线段P1P2的中点为P,设直线m的斜率为k1(![]() ),直线OP的斜率为k2,则k1k2的值为 ( )
),直线OP的斜率为k2,则k1k2的值为 ( )
A.2 B.-2 C.![]() D.-
D.-![]()
11.离心率![]() ,一个焦点是
,一个焦点是![]() 的椭圆标准方程为 ___________ .
的椭圆标准方程为 ___________ .
12.与椭圆4 x 2 + 9 y 2 = 36 有相同的焦点,且过点(-3,2)的椭圆方程为_______________.
13.已知![]() 是椭圆
是椭圆![]() 上的点,则
上的点,则![]() 的取值范围是________________ .
的取值范围是________________ .
14.已知椭圆E的短轴长为6,焦点F到长轴的一个端点的距离等于9,则椭圆E的离心率等于__________________.
15.已知椭圆的对称轴为坐标轴,离心率![]() ,短轴长为
,短轴长为![]() ,求椭圆的方程.
,求椭圆的方程.
16.过椭圆![]() 引两条切线PA、PB、A、
引两条切线PA、PB、A、
B为切点,如直线AB与x轴、y轴交于M、N两点.
(1)若![]() ,求P点坐标;
,求P点坐标;
(2)求直线AB的方程(用![]() 表示);
表示);
(3)求△MON面积的最小值.(O为原点)
17.椭圆![]()
![]() >
>![]() >
>![]() 与直线
与直线![]() 交于
交于![]() 、
、![]() 两点,且
两点,且![]() ,其中
,其中![]() 为坐标原点.
为坐标原点.
(1)求![]() 的值;
的值;
(2)若椭圆的离心率![]() 满足
满足![]() ≤
≤![]() ≤
≤![]() ,求椭圆长轴的取值范围.
,求椭圆长轴的取值范围.
18.一条变动的直线L与椭圆![]() +
+![]() =1交于P、Q两点,M是L上的动点,满足关系MP·MQ=2.若直线L在变动过程中始终保持其斜率等于1.求动点M的轨迹方程,并说明曲线的形状.
=1交于P、Q两点,M是L上的动点,满足关系MP·MQ=2.若直线L在变动过程中始终保持其斜率等于1.求动点M的轨迹方程,并说明曲线的形状.
![]() 选修1-1
第2章 圆锥曲线与方程
选修1-1
第2章 圆锥曲线与方程
§2.3双曲线
重难点:建立并掌握双曲线的标准方程,能根据已知条件求双曲线的标准方程;掌握双曲线的简单几何性质,能运用双曲线的几何性质处理一些简单的实际问题.
经典例题:已知不论b取何实数,直线y=kx+b与双曲线![]() 总有公共点,试求实数k的取值范围.
总有公共点,试求实数k的取值范围.
当堂练习:
1.到两定点![]() 、
、![]() 的距离之差的绝对值等于6的点
的距离之差的绝对值等于6的点![]() 的轨迹 ( )
的轨迹 ( )
A.椭圆 B.线段 C.双曲线 D.两条射线
2.方程![]() 表示双曲线,则
表示双曲线,则![]() 的取值范围是 ( )
的取值范围是 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]() 或
或![]()
3. 双曲线![]() 的焦距是 ( )
的焦距是 ( )
A.4 B.![]() C.8 D.与
C.8 D.与![]() 有关
有关
 4.已知m,n为两个不相等的非零实数,则方程mx-y+n=0与nx2+my2=mn所表示的曲线可
4.已知m,n为两个不相等的非零实数,则方程mx-y+n=0与nx2+my2=mn所表示的曲线可
能是 ( )
A B C D
5. 双曲线的两条准线将实轴三等分,则它的离心率为 ( )
A.![]() B.3 C.
B.3 C.![]() D.
D.
![]()
6.焦点为![]() ,且与双曲线
,且与双曲线![]() 有相同的渐近线的双曲线方程是 (
)
有相同的渐近线的双曲线方程是 (
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.若![]() ,双曲线
,双曲线![]() 与双曲线
与双曲线![]() 有 (
)
有 (
)
A.相同的虚轴 B.相同的实轴 C.相同的渐近线 D. 相同的焦点
8.过双曲线![]() 左焦点F1的弦AB长为6,则
左焦点F1的弦AB长为6,则![]() (F2为右焦点)的周长是( )
(F2为右焦点)的周长是( )
A.28 B.22 C.14 D.12
9.已知双曲线方程为![]() ,过P(1,0)的直线L与双曲线只有一个公共点,则L的条数共有
( )
,过P(1,0)的直线L与双曲线只有一个公共点,则L的条数共有
( )
A.4条 B.3条 C.2条 D.1条
10.给出下列曲线:①4x+2y-1=0; ②x2+y2=3;
③![]() ④
④![]() ,其中与直线
,其中与直线
y=-2x-3有交点的所有曲线是 ( )
A.①③ B.②④ C.①②③ D.②③④
11.双曲线![]() 的右焦点到右准线的距离为__________________________.
的右焦点到右准线的距离为__________________________.
12.与椭圆![]() 有相同的焦点,且两准线间的距离为
有相同的焦点,且两准线间的距离为![]() 的双曲线方程为____________.
的双曲线方程为____________.
13.直线![]() 与双曲线
与双曲线![]() 相交于
相交于![]() 两点,则
两点,则![]() =__________________.
=__________________.
14.过点![]() 且被点M平分的双曲线
且被点M平分的双曲线![]() 的弦所在直线方程为
.
的弦所在直线方程为
.
15.求一条渐近线方程是![]() ,一个焦点是
,一个焦点是![]() 的双曲线标准方程,并求此双曲线的离心率.
的双曲线标准方程,并求此双曲线的离心率.
16.双曲线![]() 的两个焦点分别为
的两个焦点分别为![]() ,
,![]() 为双曲线上任意一点,求证:
为双曲线上任意一点,求证:![]() 成等比数列(
成等比数列(![]() 为坐标原点).
为坐标原点).
17.已知动点P与双曲线x2-y2=1的两个焦点F1,F2的距离之和为定值,且cos∠F1PF2的最小值为-.
(1)求动点P的轨迹方程;
(2)设M(0,-1),若斜率为k(k≠0)的直线l与P点的轨迹交于不同的两点A、B,若要使MA=MB,试求k的取值范围.
18.某中心接到其正东、正西、正北方向三个观测点的报告:正西、正北两个观测点同时听到了一声巨响,正东观测点听到的时间比其他两观测点晚4s. 已知各观测点到该中心的距离都是1020m. 试确定该巨响发生的位置.(假定当时声音传播的速度为340m/ s :相关各点均在同一平面上).
![]() 选修1-1
第2章 圆锥曲线与方程
选修1-1
第2章 圆锥曲线与方程
§2.4抛物线
重难点:建立并掌握抛物线的标准方程,能根据已知条件求抛物线的标准方程;掌握抛物线的简单几何性质,能运用抛物线的几何性质处理一些简单的实际问题.
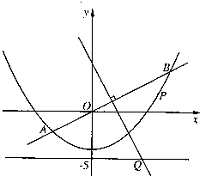 经典例题:如图, 直线y=
经典例题:如图, 直线y=![]() x与抛物线y=
x与抛物线y=![]() x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点. (1)求点Q的坐标;(2)当P为抛物线上位于线段AB下方(含A、B)的动点时, 求ΔOPQ面积的最大值.
x2-4交于A、B两点, 线段AB的垂直平分线与直线y=-5交于Q点. (1)求点Q的坐标;(2)当P为抛物线上位于线段AB下方(含A、B)的动点时, 求ΔOPQ面积的最大值.
当堂练习:
1.抛物线![]() 的焦点坐标是
( )
的焦点坐标是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.
![]()
2.已知抛物线的顶点在原点,焦点在y轴上,其上的点![]() 到焦点的距离为5,则抛物线方程为( )
到焦点的距离为5,则抛物线方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.抛物线![]() 截直线
截直线![]() 所得弦长等于
( )
所得弦长等于
( )
A.![]() B.
B.![]() C.
C.![]() D.15
D.15
4.顶点在原点,坐标轴为对称轴的抛物线过点(-2,3),则它的方程是 ( )
A.![]() 或
或![]() B.
B.![]() 或
或![]()
C.![]() D.
D.![]()
5.点![]() 到曲线
到曲线![]() (其中参数
(其中参数![]() )上的点的最短距离为 ( )
)上的点的最短距离为 ( )
A.0 B.1 C.![]() D.2
D.2
6.抛物线![]() 上有
上有![]()
![]() 三点,
三点,![]() 是它的焦点,若
是它的焦点,若![]() 成等差数列,则
( )
成等差数列,则
( )
A.![]() 成等差数列 B.
成等差数列 B.![]() 成等差数列
成等差数列
C.![]() 成等差数列 D.
成等差数列 D.![]() 成等差数列
成等差数列
7.若点A的坐标为(3,2),![]() 为抛物线
为抛物线![]() 的焦点,点
的焦点,点![]() 是抛物线上的一动点,则
是抛物线上的一动点,则![]() 取得最小值时点
取得最小值时点![]() 的坐标是
( )
的坐标是
( )
A.(0,0) B.(1,1) C.(2,2) D.![]()
8.已知抛物线![]() 的焦点弦
的焦点弦![]() 的两端点为
的两端点为![]() ,
,![]() ,则关系式
,则关系式
![]() 的值一定等于
( )
的值一定等于
( )
A.4p B.-4p C.p2 D.-p
9.过抛物线![]() 的焦点F作一直线交抛物线于P,Q两点,若线段PF与FQ的长分别是
的焦点F作一直线交抛物线于P,Q两点,若线段PF与FQ的长分别是![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.若AB为抛物线y2=2px (p>0)的动弦,且AB=a (a>2p),则AB的中点M到y轴的最近距离是 ( )
A.![]() a B.
a B.![]() p C.
p C.![]() a+
a+![]() p D.
p D.![]() a-
a-![]() p
p
11.抛物线![]() 上到其准线和顶点距离相等的点的坐标为 ______________.
上到其准线和顶点距离相等的点的坐标为 ______________.
12.已知圆![]() ,与抛物线
,与抛物线![]() 的准线相切,则
的准线相切,则![]() ___________.
___________.
13.如果过两点![]() 和
和![]() 的直线与抛物线
的直线与抛物线![]() 没有交点,那么实数a的取值范围是
.
没有交点,那么实数a的取值范围是
.
14.对于顶点在原点的抛物线,给出下列条件;
(1)焦点在y轴上; (2)焦点在x轴上;
(3)抛物线上横坐标为1的点到焦点的距离等于6;(4)抛物线的通径的长为5;
(5)由原点向过焦点的某条直线作垂线,垂足坐标为(2,1).
其中适合抛物线y2=10x的条件是(要求填写合适条件的序号) ______.
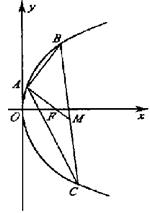 15.已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线
15.已知点A(2,8),B(x1,y1),C(x2,y2)在抛物线![]() 上,△ABC的重心与此抛物线的焦点F重合(如图)
上,△ABC的重心与此抛物线的焦点F重合(如图)
(1)写出该抛物线的方程和焦点F的坐标;
(2)求线段BC中点M的坐标;
(3)求BC所在直线的方程.
16.已知抛物线y=ax2-1上恒有关于直线x+y=0对称的相异两点,求a的取值范围.
17.抛物线x2=4y的焦点为F,过点(0,-1)作直线L交抛物线A、B两点,再以AF、BF为邻边作平行四边形FARB,试求动点R的轨迹方程.
18.已知抛物线C:![]() ,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
,过C上一点M,且与M处的切线垂直的直线称为C在点M的法线.
(1)若C在点M的法线的斜率为![]() ,求点M的坐标(x0,y0);
,求点M的坐标(x0,y0);
(2)设P(-2,a)为C对称轴上的一点,在C上是否存在点,使得C在该点的法线通过点P?若有,求出这些点,以及C在这些点的法线方程;若没有,请说明理由.
![]() 选修1-1
第2章 圆锥曲线与方程
选修1-1
第2章 圆锥曲线与方程
§2.5圆锥曲线单元测试
1)如果实数![]() 满足等式
满足等式![]() ,那么
,那么![]() 的最大值是( )
的最大值是( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
2)若直线![]() 与圆
与圆![]() 相切,则
相切,则![]() 的值为( )
的值为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3)已知椭圆![]()
![]() 的两个焦点为
的两个焦点为![]() 、
、![]() ,且
,且![]() ,弦AB过点
,弦AB过点![]() ,则△
,则△![]() 的周长为( )
的周长为( )
(A)10 (B)20 (C)2![]() (D)
(D) ![]()
4)椭圆![]() 上的点P到它的左准线的距离是10,那么点P 到它的右焦点的距离是( )
上的点P到它的左准线的距离是10,那么点P 到它的右焦点的距离是( )
(A)15 (B)12 (C)10 (D)8
5)椭圆![]() 的焦点
的焦点![]() 、
、![]() ,P为椭圆上的一点,已知
,P为椭圆上的一点,已知![]() ,则△
,则△![]() 的面积为( )
的面积为( )
(A)9 (B)12 (C)10 (D)8
6)椭圆![]() 上的点到直线
上的点到直线![]() 的最大距离是( )
的最大距离是( )
(A)3(B)![]() (C)
(C)![]() (D)
(D)![]()
7)以坐标轴为对称轴、渐近线互相垂直、两准线间距离为2的双曲线方程是( )
(A)![]() (B)
(B)![]()
(C)![]() 或
或![]() (D)
(D)![]() 或
或![]()
8)双曲线![]() 右支点上的一点P到右焦点的距离为2,则P点到左准线的距离为( )
右支点上的一点P到右焦点的距离为2,则P点到左准线的距离为( )
(A)6 (B)8 (C)10 (D)12
9)过双曲线![]() 的右焦点F2有一条弦PQ,PQ=7,F1是左焦点,那么△F1PQ的周长为( )
的右焦点F2有一条弦PQ,PQ=7,F1是左焦点,那么△F1PQ的周长为( )
(A)28 (B)![]() (C)
(C)![]() (D)
(D)![]()
10)双曲线虚轴上的一个端点为M,两个焦点为F1、F2,![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
11)过抛物线![]() (a>0)的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别为p、q,则
(a>0)的焦点F作一直线交抛物线于P、Q两点,若线段PF与FQ的长分别为p、q,则![]() 等于( )
等于( )
(A)2a
(B)![]() (C)
(C)![]()
![]() (D)
(D)![]()
12) 如果椭圆![]() 的弦被点(4,2)平分,则这条弦所在的直线方程是( )
的弦被点(4,2)平分,则这条弦所在的直线方程是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
13)与椭圆![]() 具有相同的离心率且过点(2,-
具有相同的离心率且过点(2,-![]() )的椭圆的标准方程是
)的椭圆的标准方程是
14)离心率![]() ,一条准线为
,一条准线为![]() 的椭圆的标准方程是
。
的椭圆的标准方程是
。
15)过抛物线![]() (p>0)的焦点F作一直线l与抛物线交于P、Q两点,作PP1、1垂直于抛物线的准线,垂足分别是P1、Q1,已知线段PF、QF的长度分别是a、b,那么P1Q1= 。
(p>0)的焦点F作一直线l与抛物线交于P、Q两点,作PP1、1垂直于抛物线的准线,垂足分别是P1、Q1,已知线段PF、QF的长度分别是a、b,那么P1Q1= 。
16)若直线l过抛物线![]() (a>0)的焦点,并且与y轴垂直,若l被抛物线截得的线段长为4,则a= 。17) 已知椭圆C的焦点F1(-
(a>0)的焦点,并且与y轴垂直,若l被抛物线截得的线段长为4,则a= 。17) 已知椭圆C的焦点F1(-![]() ,0)和F2(
,0)和F2(![]() ,0),长轴长6,设直线
,0),长轴长6,设直线![]() 交椭圆C于A、B两点,求线段AB的中点坐标。
交椭圆C于A、B两点,求线段AB的中点坐标。
18) 已知双曲线与椭圆![]() 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为![]() ,求双曲线方程.
,求双曲线方程.
19) 抛物线![]() 上的一点P(x , y)到点A(a,0)(a∈R)的距离的最小值记为
上的一点P(x , y)到点A(a,0)(a∈R)的距离的最小值记为![]() ,求
,求![]() 的表达式.
的表达式.
20)求两条渐近线为![]() 且截直线
且截直线![]() 所得弦长为
所得弦长为![]() 的双曲线方程.
的双曲线方程.
21)已知直线y=ax+1与双曲线3x2-y2=1交于A、B两点,(1)若以AB线段为直径的圆过坐标原点,求实数a的值。(2)是否存在这样的实数a,使A、B两点关于直线![]() 对称?说明理由.
对称?说明理由.
![]() 选修1-1
第3章 导数及其运用
选修1-1
第3章 导数及其运用
§3.1导数概念及其几何意义
重难点:了解导数概念的实际背景,理解导数的几何意义.
考纲要求:①了解导数概念的实际背景.
②理解导数的几何意义.
经典例题:利用导数的定义求函数y=x(x≠0)的导数.
当堂练习:
1、在函数的平均变化率的定义中,自变量的的增量![]() 满足( )
满足( )
A ![]() >0 B
>0 B ![]() <0
C
<0
C ![]()
![]() D
D ![]() =0
=0
2、设函数![]() ,当自变量
,当自变量![]() 由
由![]() 改变到
改变到![]() 时,函数值的改变量是( )
时,函数值的改变量是( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
3、已知函数![]() 的图像上一点(1,2)及邻近一点
的图像上一点(1,2)及邻近一点![]() ,则
,则![]() 等于( )
等于( )
A 2 B 2![]() C
C ![]() D 2+
D 2+![]()
4、质点运动规律![]() ,则在时间
,则在时间![]() 中,相应的平均速度是( )
中,相应的平均速度是( )
A ![]() B
B ![]() C
C ![]() D
D ![]()
5.函数y=f(x)在x=x0处可导是它在x=x0处连续的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.在曲线y=2x2-1的图象上取一点(1,1)及邻近一点(1+Δx,1+Δy),则![]() 等于
等于
A.4Δx+2Δx2 B.4+2Δx C.4Δx+Δx2 D.4+Δx
7.若曲线y=f(x)在点(x0,f(x0))处的切线方程为2x+y-1=0,则
A.f′(x0)>0 B.f′(x0)<0 C.f′(x0)=0 D.f′(x0)不存在
8.已知命题p:函数y=f(x)的导函数是常数函数;命题q:函数y=f(x)是一次函数,则命题p是命题q的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
9.设函数f(x)在x0处可导,则![]()
![]() 等于
等于
A.f′(x0) B.0 C.2f′(x0) D.-2f′(x0)
10.设f(x)=x(1+x),则f′(0)等于
A.0 B.1 C.-1 D.不存在
11.若曲线上每一点处的切线都平行于x轴,则此曲线的函数必是___.
12.两曲线y=x2+1与y=3-x2在交点处的两切线的夹角为___________.
13.设f(x)在点x处可导,a、b为常数,则![]()
![]() =_____.
=_____.
14.一球沿一斜面自由滚下,其运动方程是s=s(t)=t2(位移单位:m,时间单位:s),求小球在t=5时的瞬时速度________.
15.已知质点M按规律s=2t2+3做直线运动(位移单位:cm,时间单位:s),
(1)当t=2,Δt=0.01时,求![]() .
.
(2)当t=2,Δt=0.001时,求![]() .
.
(3)求质点M在t=2时的瞬时速度.
16.已知曲线y=2x2上一点A(1,2),求(1)点A处的切线的斜率.(2)点A处的切线方程.
17.已知函数f(x)=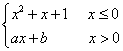
![]() ,试确定a、b的值,使f(x)在x=0处可导.
,试确定a、b的值,使f(x)在x=0处可导.
18.设f(x)=![]() ,求f′(1).
,求f′(1).
![]() 选修1-1
第3章 导数及其运用
选修1-1
第3章 导数及其运用
§3.2导数的运算
重难点:能根据定义求几个简单函数的导数,能利用导数公式表及导数的四则运算法则求简单函数的导数.
考纲要求:①能根据导数定义,求函数![]() 的导数.
的导数.
②能利用表1给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数.
表1:常见基本初等函数的导数公式和常用导数运算公式:
![]()
![]()
法则1 ![]() 法则2
法则2 ![]()
法则3 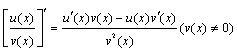
经典例题:求曲线y=![]() 在原点处切线的倾斜角.
在原点处切线的倾斜角.
当堂练习:
1.函数f(x)=a4+5a2x2-x6的导数为 ( )
A.4a3+10ax2-x6 B.4a3+10a2x-6x5
C.10a2x-6x5 D.以上都不对
2.函数y=3x(x2+2)的导数是( )
A.3x2+6 B.6x2 C.9x2+6 D.6x2+6
3.函数y=(2+x3)2的导数是( )
A.6x5+12x2 B.4+2x3 C.2(2+x3)3 D.2(2+x3)· 3x
4.函数y=x-(2x-1)2的导数是( )
A.3-4x B.3+4x C.5+8x D.5-8x
5.设函数f(x)=ax3+3x2+2,若f'(-1)=4,则a的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.函数y=![]() 的导数是( )
的导数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.函数y=![]() 的导数是( )
的导数是( )
A.![]() B.0
C.
B.0
C.![]() D.
D.![]()
8.函数y=![]() 的导数是( )
的导数是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
9.函数f(x)=![]() 的导数是 ( )
的导数是 ( )
A.![]() B.
B.
![]()
C. ![]() D.
D.
![]()
106.曲线y=-![]() x3+2x2-6在x=2处的导数为( )
x3+2x2-6在x=2处的导数为( )
A.3 B.4 C.5 D.6
11.曲线y=x2(x2-1)2+1在点(-1,1)处的切线方程为_________.
12.函数y=xsinx-cosx的导数为_________.
13.若f(x)=xcosx+![]() ,则f'(x)=_________.
,则f'(x)=_________.
14.若f(x)=cotx,则f'(x)=_________.
15.求曲线y=2x3-3x2+6x-1在x=1及x=-1处两切线的夹角.
16.已知函数f(x)=x2(x-1),若f'(x0)=f(x0),求x0的值.
17.已知函数y=![]() ,求在x=1时的导数.
,求在x=1时的导数.
18.求函数y=![]() 的导数.
的导数.
![]() 选修1-1
第3章 导数及其运用
选修1-1
第3章 导数及其运用
§3.3导数在研究函数中的应用
重难点:了解函数单调性和导数的关系;能利用导数研究函数的单调性,会求函数的单调区间,对多项式函数一般不超过三次;了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、极小值,对多项式函数一般不超过三次;会求闭区间上函数的最大值、最小值,对多项式函数一般不超过三次.
考纲要求:①了解函数单调性和导数的关系;能利用导数研究函数的单调性,会求函数的单调区间,对多项式函数一般不超过三次.
②了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、极小值,对多项式函数一般不超过三次;会求闭区间上函数的最大值、最小值,对多项式函数一般不超过三次.
经典例题:已知函数![]() 与
与![]() 的图象都过点P
的图象都过点P![]() 且在点P处有相
且在点P处有相
同的切线.
(1) 求实数![]() 的值;
的值;
(2) 设函数![]() , 求
, 求![]() 的单调区间, 并指出
的单调区间, 并指出![]() 在该区间上的单调性.
在该区间上的单调性.
当堂练习:
1. 函数![]() 是减函数的区间为 ( )
是减函数的区间为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
2. 函数![]() , 已知
, 已知![]() 在
在![]() 时取得极值, 则
时取得极值, 则![]() ( )
( )
A. 2 B. 3 C. 4 D. 5
3. 在函数![]() 的图象上, 其切线的倾斜角小于
的图象上, 其切线的倾斜角小于![]() 的点中, 坐标为整数的点的个数是
的点中, 坐标为整数的点的个数是
( )
A. 3 B. 2 C. 1 D. 0
4. 函数![]() 的图象与直线
的图象与直线![]() 相切, 则
相切, 则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
1
D.
1
5. 已知函数![]() (m为常数) 图象上点A处的切线与直线
(m为常数) 图象上点A处的切线与直线![]()
的夹角为![]() , 则点A的横坐标为
( )
, 则点A的横坐标为
( )
A. 0
B.
1
C. 0或![]() D. 1或
D. 1或![]()
6. 曲线![]()
![]() 在
在![]() 处的切线的斜率为
( )
处的切线的斜率为
( )
A. 7 B. 6 C. 5 D. 4
7. 已知某物体的运动方程是![]()
![]()
![]() , 则当
, 则当![]() 时的瞬时速度是
( )
时的瞬时速度是
( )
A. 10m /s B. 9m /s C. 4m /s D. 3m /s
8. 函数![]() =
=![]() 在区间
在区间![]() 上的最大值与最小值分别是
( )
上的最大值与最小值分别是
( )
A. 5, 4 B. 13, 4 C. 68, 4 D. 68, 5
9. 已知函数y=-x 2-2x+3在区间![]() 上的最大值为
上的最大值为![]() , 则a等于
( )
, 则a等于
( )
A. -![]() B.
B. ![]() C. -
C. -![]() D. -
D. -![]() 或-
或-![]()
10. 若函数y=x 3-2x 2+mx, 当x=![]() 时, 函数取得极大值, 则m的值为
( )
时, 函数取得极大值, 则m的值为
( )
A. 3
B. 2
C. 1
D. ![]()
11. 曲线![]() 在点
在点![]() 处的切线与x轴、直线
处的切线与x轴、直线![]() 所围成的三角形的面积为
.
所围成的三角形的面积为
.
12. 曲线![]() 在点
在点![]() 处的切线方程是
.
处的切线方程是
.
13. 与直线![]() =0平行, 且与曲线y=
=0平行, 且与曲线y=![]() 相切的直线方程为
.
相切的直线方程为
.
14. 曲线y=![]() 在点M
在点M![]() 处的切线的斜率为-1, 则a=
.
处的切线的斜率为-1, 则a=
.
15. 已知函数![]()
(1) 求![]() 的单调递减区间;
的单调递减区间;
(2) 若![]() 在区间
在区间![]() 上的最大值为20, 求它在该区间上的最小值.
上的最大值为20, 求它在该区间上的最小值.
16. 已知函数![]() 的图象过点P
的图象过点P![]() , 且在点M
, 且在点M![]() 处的切线
处的切线
方程为![]() .
.
(1) 求函数![]() 的解析式; (2) 求函数
的解析式; (2) 求函数![]() 的单调区间.
的单调区间.
17. 已知函数![]() 当
当![]() 时, y的极值为3.
时, y的极值为3.
求: (1) a, b的值; (2) 该函数单调区间.
18. 设函数![]() 若对于任意
若对于任意![]() 都有
都有![]() 成立, 求实数
成立, 求实数![]() 的
的
取值范围.
![]() 选修1-1
第3章 导数及其运用
选修1-1
第3章 导数及其运用
§3.4生活中的优化问题
重难点:会利用导数解决某些实际问题.
考纲要求:①会利用导数解决某些实际问题.
经典例题:某制造商制造并出售球形瓶装的某种饮料.瓶子的制造成本是0.8πr2分(其中r是瓶子的半径,单位是厘米).已知每出售1 mL的饮料,制造商可获利0.2分,且制造商能制作的瓶子的最大半径为6 cm.
(1)瓶子半径多大时,能使每瓶饮料的利润最大?
(2)瓶子半径多大时,每瓶饮料的利润最小?
当堂练习:
1.函数y=x3+x的单调增区间为( )
A.(-∞,+∞) B.(0,+∞)
C.(-∞,0) D.不存在
2.若函数f(x)=x2+bx+c的图象的顶点在第四象限,则函数f′(x)的图象是( )
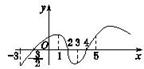
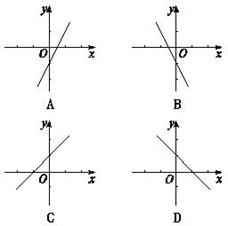
3.右上图是函数y=f(x)的导函数y=f′(x)的图象,则下面判断正确的是 ( )
A.在区间(-2,1)内f(x)是增函数 B.在(1,3)内f(x)是减函数
C.在(4,5)内f(x)是增函数 D.在x=2时f(x)取到极小值
4.下列说法正确的是( )
A.函数在闭区间上的极大值一定比极小值大 B.函数在闭区间上的最大值一定是极大值
C.对于f(x)=x3+px2+2x+1,若p<![]() ,则f(x)无极值 D.函数f(x)在区间(a,b)上一定存在最值
,则f(x)无极值 D.函数f(x)在区间(a,b)上一定存在最值
5.若函数f(x)=x3-ax2+1在(0,2)内单调递减,则实数a的取值范围是( )
A.a≥3 B.a=2 C.a≤3 D.0<a<3
6.★若f(x)=ax3+bx2+cx+d(a>0)在R上是增函数,则( )
A.b2-4ac>0 B.b>0,c>0
C.b=0,c>0 D.b2-3ac<0
7.已知函数f(x)=ax3+(2a-1)x2+2,若x=-1是y=f(x)的一个极值点,则a的值为( )
A.2
B.-2
C.![]() D.4
D.4
8.在区间(0,+∞)内,函数y=ex-x是( )
A.增函数 B.减函数 C.先增后减 D.先减后增
9.函数y=f(x)=lnx-x在区间(0,e]上的最大值为( )
A.1-e B.-1 C.-e D.0
10.函数y=x5-x3-2x,则下列判断正确的是( )
A.在区间(-1,1)内函数为增函数 B.在区间(-∞,-1)内函数为减函数
C.在区间(-∞,1)内函数为减函数 D.在区间(1,+∞)内函数为增函数
11.函数f(x)=x3-3x2+7的极大值是 .
12.函数y=4x2+![]() 的单调增区间为 .
的单调增区间为 .
13.函数y=3x2-2lnx的单调减区间为 .
14.函数y=x4-8x2+2在[-1,3]上的最大值为 .
15.已知函数y=ax与y=-![]() 在区间(0,+∞)上都是减函数,试确定函数y=ax3+bx2+5的单调区间.
在区间(0,+∞)上都是减函数,试确定函数y=ax3+bx2+5的单调区间.
16.当室内的有毒细菌开始增加时,就要使用杀菌剂.刚开始使用的时候,细菌数量还会继续增加,随着时间的增加,它增加幅度逐渐变小,到一定时间,细菌数量开始减少.如果使用杀菌剂t小时后的细菌数量为b(t)=105+104t-103t2.
(1)求细菌在t=5与t=10时的瞬时速度;
(2)细菌在哪段时间增加,在哪段时间减少?为什么?
17.已知a为实数,f(x)=(x2-4)(x-a).
(1)求导数f′(x);(2)若f′(-1)=0,求f(x)在[-2,2]上的最大值和最小值.
18.某产品按质量分为10个档次,生产第一档(即最低档次)的利润是每件8元,每提高一个档次,利润每件增加2元,但在相同的时间内产量减少3件.在相同的时间内,最低档的产品可生产60件.问在相同的时间内,生产第几档次的产品的总利润最大?有多少元?
![]() 选修1-1
第3章 导数及其运用
选修1-1
第3章 导数及其运用
§3.5导数及其运用单元测试
1、设![]() 是可导函数,且
是可导函数,且![]() ( )
( )
A.![]() B.-1 C.0 D.-2
B.-1 C.0 D.-2
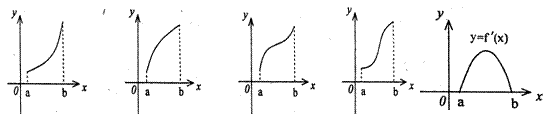 2、f/(x)是f(x)的导函数,f/(x)的图象如右图所示,则f(x)的图象只可能是( )
2、f/(x)是f(x)的导函数,f/(x)的图象如右图所示,则f(x)的图象只可能是( )
(A) (B) (C) (D)
3、下列函数中,在![]() 上为增函数的是
( )
上为增函数的是
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、已知![]() 是R上的单调增函数,则
是R上的单调增函数,则![]() 的取值范围是 ( )
的取值范围是 ( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
5、已知函数![]() 在
在![]() 上是单调函数,则实数
上是单调函数,则实数![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
6、下列说法正确的是 ( )
A. 函数在闭区间上的极大值一定比极小值大;
B. 函数在闭区间上的最大值一定是极大值;
C. 对于![]() ,若
,若![]() ,则
,则![]() 无极值;
无极值;
D.函数![]() 在区间
在区间![]() 上一定存在最值.
上一定存在最值.
7、函数![]() 在
在![]() 处有极值10, 则点
处有极值10, 则点![]() 为
( )
为
( )
A.![]() B.
B.![]() C.
C. ![]() 或
或![]() D.不存在
D.不存在
8、定义在闭区间![]() 上的连续函数
上的连续函数![]() 有唯一的极值点
有唯一的极值点![]() ,且
,且![]() ,则下列说法正确的是
( )
,则下列说法正确的是
( )
A.函数![]() 有最小值
有最小值![]() B. 函数
B. 函数![]() 有最小值,但不一定是
有最小值,但不一定是![]()
C.函数![]() 的最大值也可能是
的最大值也可能是![]() D. 函数
D. 函数![]() 不一定有最小值
不一定有最小值
9、函数![]() 在[0,3]上的最大值和最小值分别是
( )
在[0,3]上的最大值和最小值分别是
( )
A. 5,15 B. 5,![]() C. 5,
C. 5,![]() D. 5,
D. 5,![]()
10、函数![]() 上最大值等于
( )
上最大值等于
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11、设函数![]() ,则
,则![]() ′
′![]() =____________________
=____________________
12、函数![]() 的单调递减区间为
的单调递减区间为
13、函数![]() 的极大值为6,极小值为2,则
的极大值为6,极小值为2,则![]() 的减区间是
的减区间是
14、点![]() 是曲线
是曲线![]() 上任意一点, 则点
上任意一点, 则点![]() 到直线
到直线![]() 的距离的最小值是
的距离的最小值是
15、已知直线![]() 为曲线
为曲线![]() 在点
在点![]() 处的切线,
处的切线,![]() 为该曲线的另一条切线,且
为该曲线的另一条切线,且![]()
![]() (Ⅰ)求直线
(Ⅰ)求直线![]() 的方程;(Ⅱ)求由直线
的方程;(Ⅱ)求由直线![]()
![]()
![]() 和
和![]() 轴所围成的三角形的面积
轴所围成的三角形的面积
16、设函数![]()
(Ⅰ)当![]() 求函数满足
求函数满足![]() 时的
时的![]() 的集合;
的集合;
(Ⅱ)求a的取值范围,使f(x)在区间(0,+∞)上是单调减函数![]()
17、设函数f(x)=x(x-1)(x-a),(a>1)
(Ⅰ)求导数f¢ (x);
(Ⅱ)若不等式f(x1)+ f(x2)£0成立,求a的取值范围
![]()
18、已知![]() 在
在![]() 时有极大值6,在
时有极大值6,在![]() 时有极小值,求
时有极小值,求![]() 的值;并求
的值;并求![]() 在区间[-3,3]上的最大值和最小值.
在区间[-3,3]上的最大值和最小值.
19、设函数![]()
(Ⅰ)求![]() 的单调区间和极值;
的单调区间和极值;
(Ⅱ)若关于![]() 的方程
的方程![]() 有3个不同实根,求实数a的取值范围.
有3个不同实根,求实数a的取值范围.
(Ⅲ)已知当![]() 恒成立,求实数k的取值范围.
恒成立,求实数k的取值范围.
![]() 选修1-1
选修1-1综合测试
选修1-1
选修1-1综合测试
1.已知命题甲:![]() ,命题乙:点
,命题乙:点![]() 是可导函数
是可导函数![]() 的极值点,则甲是乙的( )
的极值点,则甲是乙的( )
A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分而不必要条件
2、已知椭圆的焦点为![]() 和
和![]() ,点
,点![]() 在椭圆上的一点,且
在椭圆上的一点,且![]() 是
是![]() 的等差中项,则该椭圆的方程为( )
的等差中项,则该椭圆的方程为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
3、已知![]() ,点P在A、B所在的平面内运动且保持
,点P在A、B所在的平面内运动且保持![]() ,则
,则![]() 的最大值和最小值分别是 ( )
的最大值和最小值分别是 ( )
A.![]() 、3 B.10、2 C.5、1 D.6、4
、3 B.10、2 C.5、1 D.6、4
4、椭圆的一焦点与短轴两顶点组成一个等边三角形,则椭圆的离心率为( )
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
5.双曲线x2-ay2=1的焦点坐标是 ( )
A.(![]() , 0) , (-
, 0) , (-![]() , 0) B.(
, 0) B.(![]() , 0), (-
, 0), (-![]() , 0)
, 0)
C.(-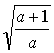 , 0),(
, 0),(![]() , 0) D.(-
, 0) D.(-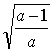 , 0), (
, 0), (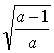 , 0)
, 0)
6、若双曲线![]() 与
与![]() 的离心率分别为
的离心率分别为![]() ,则当
,则当![]() 变化时,
变化时,![]() 的最小值是( )
的最小值是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.曲线y=x3+x-2在点P0处的切线平行于直线y=4x-1,则P0的坐标可能是( )
A.(0,1) B.(1,0) C.(-1,0) D.(1,4)
8. 函数![]() 在区间
在区间![]() 上单调递增,那么实数a的取值范围是( )
上单调递增,那么实数a的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9、方程x3-6x2+9x-10=0的实根个数是 ( )
A、3 B、2 C、1 D、0
10.已知函数f(x)的导函数![]() 的图像如左图所示,那么函数f(x)的图像最有可能的是( )
的图像如左图所示,那么函数f(x)的图像最有可能的是( )
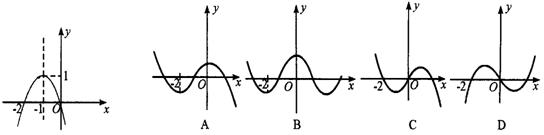
11.命题![]() 的否命题是
.
的否命题是
.
12.已知p是r的充分不必要条件,s是r的必要条件,q是s的必要条件,那么p是q成立的 条件。(填“充分不必要”“必要不充分”、“充要”或“既不充分也不必要” )
13.若方程![]() 所表示的曲线为C,给出下列四个命题:
所表示的曲线为C,给出下列四个命题:
①若C为椭圆,则1<t<4; ②若C为双曲线,则t>4或t<1;
③曲线C不可能是圆; ④若C表是椭圆,且长轴在x轴上,则![]() .其中真命题的序号为
(把所有正确命题的序号都填在横线上)
.其中真命题的序号为
(把所有正确命题的序号都填在横线上)
14.函数y=![]() 的单调增区间是 ,减区间是 .
的单调增区间是 ,减区间是 .
15.求与椭圆![]() 有共同焦点,且过点
有共同焦点,且过点![]() 的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率。
的双曲线方程,并且求出这条双曲线的实轴长、焦距、离心率。
16.设椭圆方程为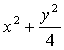 =1,过点M(0,1)的直线l交椭圆于点A、B,O为坐标原点,点P满足
=1,过点M(0,1)的直线l交椭圆于点A、B,O为坐标原点,点P满足![]() ,当l绕点M旋转时,求动点P的轨迹方程.
,当l绕点M旋转时,求动点P的轨迹方程.
17.设f(x)=x3-![]() x2-2x+5
x2-2x+5
(1)求函数f(x)的单调区间。(2)求极值点与极值。
18.已知椭圆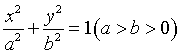 的离心率
的离心率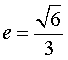 ,过点
,过点![]() 和
和![]() 的直线与原点的距离为
的直线与原点的距离为![]() 。
。
⑴求椭圆的方程;
⑵已知定点![]() ,若直线
,若直线![]() 与椭圆交于
与椭圆交于![]() 两点,问:是否存在
两点,问:是否存在![]() 的值,使以
的值,使以![]() 为直径的圆过
为直径的圆过![]() 点?请说明理由。
点?请说明理由。
选修1-1参考答案
第1章 常用逻辑用语
§1.1命题及其关系
经典例题:【 解析】由![]() ,得
,得![]() .
. ![]()
![]() :
:![]() .
.
由![]() ,得
,得![]() .
.
![]()
![]() :B={
:B={![]() }.
}.
∵![]() 是
是![]() 的充分非必要条件,且
的充分非必要条件,且![]() ,
, ![]() A
A![]() B.
B.
![]()
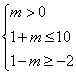 即
即![]()
当堂练习:
1.C; 2.B;
3.A; 4.C; 5.C; 6.C; 7.C; 8.D; 9.B; 10.C; 11. ②; 12. ①④⑤⑥; 13. m=![]() (也可为
(也可为![]() 或0);14. 充分不必要.
或0);14. 充分不必要.
15. 【 解析】 (1)逆命题:若x=0,或y=0则xy=0;否命题:xy≠0,则x≠0且y≠0;
逆否命题:若x≠0,且 y≠0则xy≠0;
(2)逆命题:若xy>0,则x>0,y>0;否命题:若x≤0,或y≤0则xy≤0;
逆否命题:若xy≤0;则 x≤0,或y≤0
16. 【 解析】 “![]() 或
或![]() ”
”![]()
![]() ,
,![]()
![]()
![]() ,因为“
,因为“![]() 或
或![]() ”
”![]()
![]() ,但
,但![]()
![]() , 故 “
, 故 “![]() 或
或![]() ”是“
”是“![]() ”的必要不充分条件.
”的必要不充分条件.
17. 【 解析】方程①有实根的充要条件是![]() 解得m
解得m![]() 1.
1.
方程②有实根的充要条件是![]() ,解得
,解得![]()
![]() 故m=-1或m=0或m=1.
故m=-1或m=0或m=1.
当m=-1时,①方程无整数解.当m=0时,②无整数解;
当m=1时,①②都有整数.从而①②都有整数解m=1.反之,m=1①②都有整数解.
∴①②都有整数解的充要条件是m=1.
18. 【 解析】根据韦达定理得a=α+β,b=αβ.判定的条件是p:![]() 结论是q:
结论是q:![]() (注意p中a、b满足的前提是
(注意p中a、b满足的前提是
Δ=a2-4b≥0)
(1)由![]() ,得a=α+β>2,b=αβ>1,∴q
,得a=α+β>2,b=αβ>1,∴q![]() p
p
(2)为证明p![]() q,可以举出反例:取α=4,β=
q,可以举出反例:取α=4,β=![]() ,它满足a=α+β=4+
,它满足a=α+β=4+![]() >2,b=αβ=4×
>2,b=αβ=4×![]() =2>1,但q不成立.
=2>1,但q不成立.
综上讨论可知a>2,b>1是α>1,β>1的必要但不充分条件.
§1.2简单的逻辑联结词
经典例题:【 解析】由已知p,q中有且仅有一为真,一为假.
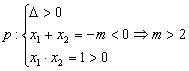 .
. ![]() .
.
(1)若p假q真,则![]() ;
;
(2)若p真q假,则![]() .
.
综上所述:![]() .
.
当堂练习:
1.C; 2.B; 3.B; 4.B; 5.A; 6.B; 7.A; 8.B; 9.B; 10.B; 11. 此题是开放性题,答案不唯一,可以是“侧棱与底面所成角相等”;或“侧面与底面所成角相等;……; 12. 6是12或24的约数;6是12的约数,也是24的约数;6不是12的约数; 13. ②;14. ②③④.
15. 【解】 ① p∨q:(2=2)∨(2>2),即2≥2.(真)
由于2=2是真命题,所以2≥2是真命题.
②p∨q:(正方形的对角线互相垂直)∨(矩形的对角线互相平分).
由于两个命题都是真的,所以p∨q是真命题.
16. 【 解析】 设使p的解集为![]() 的
的![]() 的集合为A,使
的集合为A,使![]() 在
在![]() 内是增函数的
内是增函数的![]() 的集合为B,则本题即求
的集合为B,则本题即求![]() 答案为
答案为![]() .
.
17. 【 解析】 若按一般思维习惯,对三条抛物线与x轴公共点情况一一分类讨论,则较为繁琐,若从其反面思考,先求“三抛物线均与x轴无公共点的![]() 的范围”则很简单.
的范围”则很简单.
由 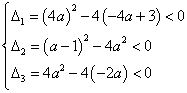 解之,得
解之,得![]()
![]() ,记
,记![]() ,
,
则所求a的范围是 ∁![]()
18. 【 解析】 ∵p且q为假∴p、q至少有一命题为假,又“非q”为假 ∴q为真,从而可知p为假.
由p为假且q为真,可得:![]()
即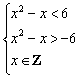 ∴
∴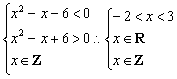
故x的取值为:-1、0、1、2.
§1.3全称量词与存在量词
经典例题:【 解析】 ⑴全称命题⑵全称命题⑶存在性命题.⑷存在性命题.
当堂练习:
1.A;
2.C; 3.C; 4.C; 5.C; 6.C; 7.A; 8.D; 9.C; 10.C; 11. ![]() ,
,![]() ; 12.
; 12. ![]() ,
,![]() ; 13.
; 13.![]() ,x∈∁RQ;14. 任意一个三角形都有外接圆
,x∈∁RQ;14. 任意一个三角形都有外接圆
15. 【 解析】 ①假命题②真命题③真命题④假命题
16. 【 解析】 ①全称命题;真命题②全称命题;假命题③存在命题;真命题④存在命题;真命题.
17. 【 解析】 ![]()
18. 【 解析】 (1)“对所有的正数x, >x-1”的否定是“存在正数x, ≤x-1”;
(2)“不存在实数x,x2+1<2x”的否定是“存在实数x,x2+1≥2x ”;
(3)“集合A中的任意一个元素都是集合B的元素”的否定是“存在集合A中的元素不是集合B中的元素”;
(4)“集合A中至少有一个元素是集合B的元素”的否定是“集合A中的所有元素都不是集合B中的元素”.
§1.4常用逻辑用语单元测试
1.D; 2.B; 3.B; 4.B; 5.A; 6.D; 7.B; 8.A; 9.D; 10.A; 11. ②④; 12. 平行四边形不一定是菱形;或至少存在一个平行四边形不是菱形; 13. 必要,充分,必要;14. 必要不充分
15.本题考查四种命题间的关系.
解:(1)逆命题:若一个四边形的对角线相等且互相平分,则它是矩形(假命题).
否命题:若一个四边形不是矩形,则它的对角线不相等或不互相平分(假命题).
逆否命题:若一个四边形的对角线不相等或不互相平分,则它不是矩形(真命题).
(2)逆命题:如果一个正数不是质数,那么这个正数是正偶数(假命题).
否命题:如果一个正数不是偶数,那么这个数是质数(假命题).
逆否命题:如果一个正数是质数,那么这个数不是偶数(假命题).
16.解:(1)根据真值表,复合命题可以写成简单形式:
p或q:连续的三个整数的乘积能被2或能被3整除.
p且q:连续的三个整数的乘积能被2且能被3整除.
非p:存在连续的三个整数的乘积不能被2整除.
∵连续的三整数中有一个(或两个)是偶数,而有一个是3的倍数,
∴p真,q真,∴p或q与p且q均为真,而非p为假.
(2)根据真值表,只能用逻辑联结词联结两个命题,不能写成简单形式:
p或q:对角线互相垂直的四边形是菱形或对角线互相平分的四边形是菱形.
p且q:对角线互相垂直的四边形是菱形且对角线互相平分的四边形是菱形.
非p:存在对角线互相垂直的四边形不是菱形.
∵p假q假,∴p或q与p且q均为假,而非p为真.
17.解:对任意实数![]() 都有
都有![]() 恒成立
恒成立![]()
![]() ;关于
;关于![]() 的方程
的方程![]() 有实数根
有实数根![]() ;如果P正确,且Q不正确,有
;如果P正确,且Q不正确,有![]() ;如果Q正确,且P不正确,有
;如果Q正确,且P不正确,有![]() 。所以实数
。所以实数![]() 的取值范围为
的取值范围为![]() 。
。
18.本题考查充要条件、充分条件、必要条件.对于这类问题,将语言叙述符号化,画出它们的综合结构图,再给予判定.
解:p、q、r、s的关系如图所示,由图可知
![]()
答案:(1)s是q的充要条件 (2)r是q的充要条件 (3)p是q的必要条件
19.证明:用反证法,假设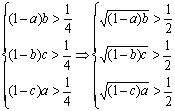 ,①+②+③得:
,①+②+③得:
![]() ,左右矛盾,故假设不成立,∴(1-a)b,(1-b)c,(1-c)a不同时大于
,左右矛盾,故假设不成立,∴(1-a)b,(1-b)c,(1-c)a不同时大于![]() .
.
20.解析:先证充分性,而必要性只需要通过举反例来否定.
先证明条件的充分性:
|
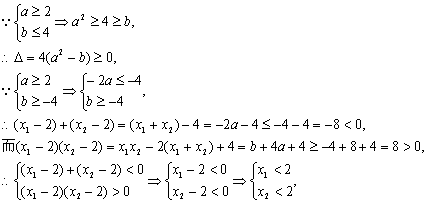
①、②知“a≥2且b≤4” ![]() “方程有实数根,且两根均小于2”.
“方程有实数根,且两根均小于2”.
再验证条件不必要:
∵方程x2-x=0的两根为x1=0, x2=1,则方程的两根均小于2,而a=-![]() <2,
<2,
∴“方程的两根小于2” ![]() “a≥2且b≤4”.
“a≥2且b≤4”.
综上,a≥2且b≤4是方程有实数根且两根均小于2的充分但不必要条件.
第2章 圆锥曲线与方程
§2.1-2椭圆
经典例题:[解析]:设A(x1,y1),B(x2,y2),![]() 由焦半径公式有a-ex1+a-ex2=
由焦半径公式有a-ex1+a-ex2=![]() ,∴x1+x2=
,∴x1+x2=![]() ,
,
即AB中点横坐标为![]() ,又左准线方程为
,又左准线方程为![]() ,∴
,∴![]() ,即a=1,∴椭圆方程为x2+
,即a=1,∴椭圆方程为x2+![]() y2=1.
y2=1.
当堂练习:
1.D;
2.D; 3.D; 4.A; 5.A; 6.D; 7.B; 8.D; 9.C; 10.D; 11. ![]() ; 12.
; 12. ![]() ; 13.
; 13. ![]() ;14.
;14. ![]() ;
;
![]()
![]() 15. [解析]:由
15. [解析]:由
![]()
![]() ,∴椭圆的方程为:
,∴椭圆的方程为:![]() 或
或![]() .
.
16.[解析]:(1)![]() ∴OAPB的正方形
∴OAPB的正方形
由
![]() ∴P点坐标为(
∴P点坐标为(![]() )
)
(2)设A(x1,y1),B(x2,y2)
则PA、PB的方程分别为![]() ,而PA、PB交于P(x0,y0)
,而PA、PB交于P(x0,y0)
即x1x0+y1y0=4,x2x0+y2y0=4,∴AB的直线方程为:x0x+y0y=4
(3)由![]() 、
、![]()
![]()
![]()
![]()
当且仅当![]() .
.
17. [解析]:设![]() ,由OP ⊥ OQ
,由OP ⊥ OQ ![]() x 1 x 2
+ y 1 y 2 = 0
x 1 x 2
+ y 1 y 2 = 0
![]() 又将
又将![]()
![]()
![]() ,
,![]()
![]() 代入①化简得
代入①化简得 ![]() .
.
(2) ![]() 又由(1)知
又由(1)知![]()
![]() ,∴长轴 2a
∈ [
,∴长轴 2a
∈ [![]() ].
].
18.[解析]:设动点M(x,y),动直线L:y=x+m,并设P(x1,y1),Q(x2,y2)是方程组![]() 的解,消去y,得3x2+4mx+2m2-4=0,其中Δ=16m2-12(2m2-4)>0,∴-
的解,消去y,得3x2+4mx+2m2-4=0,其中Δ=16m2-12(2m2-4)>0,∴-![]() <m<
<m<![]() ,且x1+x2=-
,且x1+x2=-![]() ,x1x2=
,x1x2=![]() ,又∵MP=
,又∵MP=![]() x-x1,MQ=
x-x1,MQ=![]() x-x2.由MPMQ=2,得x-x1x-x2=1,也即
x-x2.由MPMQ=2,得x-x1x-x2=1,也即
x2-(x1+x2)x+x1x2=1,于是有![]() ∵m=y-x,∴x2+2y2-4=3.由x2+2y2-4=3,得椭圆
∵m=y-x,∴x2+2y2-4=3.由x2+2y2-4=3,得椭圆![]() 夹在直线
夹在直线![]() 间两段弧,且不包含端点.由x2+2y2-4=-3,得椭圆x2+2y2=1.
间两段弧,且不包含端点.由x2+2y2-4=-3,得椭圆x2+2y2=1.
§2.3双曲线
经典例题:[解析]:联立方程组![]() 消去y得(2k2-1)x2+4kbx+(2b2+1)=0,
消去y得(2k2-1)x2+4kbx+(2b2+1)=0,
当![]() 若b=0,则k
若b=0,则k![]() ;若
;若![]() ,不合题意.
,不合题意.
当![]() 依题意有△=(4kb)2-4(2k2-1)(2b2+1)>0,
依题意有△=(4kb)2-4(2k2-1)(2b2+1)>0,![]() 对所有实数b恒成立,
对所有实数b恒成立,![]() ∴2k2<1,得
∴2k2<1,得![]() .
.
当堂练习:
1.D;
2.D; 3.C; 4.C; 5.B; 6.B; 7.D; 8.A; 9.B; 10.D; 11. ![]() ; 12.
; 12. ![]() ; 13.
; 13. ![]() ;14.
;14. ![]() ;
;
15.[解析]:设双曲线方程为:![]() ,∵双曲线有一个焦点为(4,0),
,∵双曲线有一个焦点为(4,0),![]()
双曲线方程化为: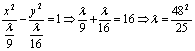 ,
,
∴双曲线方程为: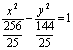 ∴
∴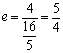 .
.
16.[解析]:易知![]() ,准线方程:
,准线方程:![]() ,设
,设![]() ,
,
则![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]() 成等比数列.
成等比数列.
17. [解析]:(1)∵x2-y2=1,∴c=.设PF1+PF2=2a(常数a>0),2a>2c=2,∴a>
由余弦定理有cos∠F1PF2===-1
∵PF1PF2≤()2=a2,∴当且仅当PF1=PF2时,PF1PF2取得最大值a2.
此时cos∠F1PF2取得最小值-1,由题意-1=-,解得a2=3,![]()
 ∴P点的轨迹方程为+y2=1.
∴P点的轨迹方程为+y2=1.
(2)设l:y=kx+m(k≠0),则由,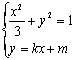 将②代入①得:(1+3k2)x2+6kmx+3(m2-1)=0
(*)
将②代入①得:(1+3k2)x2+6kmx+3(m2-1)=0
(*)
设A(x1,y1),B(x2,y2),则AB中点Q(x0,y0)的坐标满足:x0=
即Q(-) ∵MA=MB,∴M在AB的中垂线上,
∴klkAB=k·=-1 ,解得m= …③ 又由于(*)式有两个实数根,知△>0,
即 (6km)2-4(1+3k2)[3(m2-1)]=12(1+3k2-m2)>0 ④ ,将③代入④得
12[1+3k2-()2]>0,解得-1<k<1,由k≠0,∴k的取值范围是k∈(-1,0)∪(0,1).
18.[解析]:以接报中心为原点O,正东、正北方向为x轴、y轴正向,建立直角坐标系.设A、B、C分别是西、东、北观测点,则A(-1020,0),B(1020,0),C(0,1020)
设P(x,y)为巨响为生点,由A、C同时听到巨响声,得PA=PB,故P在AC的垂直平分线PO上,PO的方程为y=-x,因B点比A点晚4s听到爆炸声,故PB- PA=340×4=1360
由双曲线定义知P点在以A、B为焦点的双曲线![]() 上, 依题意得a=680, c=1020,
上, 依题意得a=680, c=1020,
![]()
![]()
用y=-x代入上式,得![]() ,∵PB>PA,
,∵PB>PA,![]()
![]() ,答:巨响发生在接报中心的西偏北45°距中心
,答:巨响发生在接报中心的西偏北45°距中心![]() 处.
处.
§2.4抛物线
![]()
![]()
![]() 经典例题:【解】(1) 解方程组
经典例题:【解】(1) 解方程组 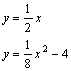 得
得 ![]() 或
或 ![]()
即A(-4,-2),B(8,4), 从而AB的中点为M(2,1).由kAB==![]() ,直线AB的垂直平分线方程
,直线AB的垂直平分线方程
y-1=![]() (x-2). 令y=-5, 得x=5,
∴Q(5,-5).
(x-2). 令y=-5, 得x=5,
∴Q(5,-5).
(2) 直线OQ的方程为x+y=0, 设P(x,
![]() x2-4).∵点P到直线OQ的距离
x2-4).∵点P到直线OQ的距离
d=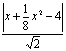 =
=![]() ,
,![]() ,∴SΔOPQ=
,∴SΔOPQ=![]()
![]() =
=![]() .
.
∵P为抛物线上位于线段AB下方的点, 且P不在直线OQ上, ∴-4≤x<4![]() -4或4
-4或4![]() -4<x≤8.
-4<x≤8.
∵函数y=x2+8x-32在区间[-4,8] 上单调递增, ∴当x=8时, ΔOPQ的面积取到最大值30.
当堂练习:
1.C;
2.D; 3.A; 4.B; 5.B; 6.A; 7.C; 8.B; 9.C; 10.D; 11. ![]() ; 12. 2; 13.
; 12. 2; 13. ![]() ;14. (2),(5);
;14. (2),(5);
15.[解析]:(1)由点A(2,8)在抛物线![]() 上,有
上,有![]() ,
,
解得p=16. 所以抛物线方程为![]() ,焦点F的坐标为(8,0).
,焦点F的坐标为(8,0).
(2)如图,由于F(8,0)是△ABC的重心,M是BC的中点,所以F是线段AM的
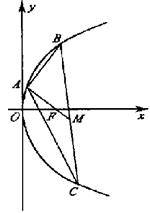 定比分点,且
定比分点,且![]() ,设点M的坐标为
,设点M的坐标为![]() ,则
,则
![]() ,解得
,解得![]() ,
,
所以点M的坐标为(11,-4).
(3)由于线段BC的中点M不在x轴上,所以BC所在
的直线不垂直于x轴.设BC所在直线的方程为:![]()
由![]() 消x得
消x得![]() ,
,
所以![]() ,由(2)的结论得
,由(2)的结论得![]() ,解得
,解得![]()
因此BC所在直线的方程为:![]()
16.[解析]:设在抛物线y=ax2-1上关于直线x+y=0对称的相异两点为P(x,y),Q(-y,-x),则
![]()
![]() ,由①-②得x+y=a(x+y)(x-y),∵P、Q为相异两点,∴x+y≠0,又a≠0,
,由①-②得x+y=a(x+y)(x-y),∵P、Q为相异两点,∴x+y≠0,又a≠0,
∴![]() ,代入②得a2x2-ax-a+1=0,其判别式△=a2-4a2(1-a)>0,解得
,代入②得a2x2-ax-a+1=0,其判别式△=a2-4a2(1-a)>0,解得![]() .
.
17.[解析]:设R(x,y),∵F(0,1), ∴平行四边形FARB的中心为![]() ,L:y=kx-1,代入抛物线方程得x2-4kx+4=0, 设A(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=4,且△=16k2-16>0,即k>1 ①,
,L:y=kx-1,代入抛物线方程得x2-4kx+4=0, 设A(x1,y1),B(x2,y2),则x1+x2=4k,x1x2=4,且△=16k2-16>0,即k>1 ①,
![]() ,∵C为AB的中点.
,∵C为AB的中点.
![]() ∴
∴ 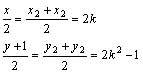
![]()
![]()
![]() ,消去k得x2=4(y+3),由① 得,
,消去k得x2=4(y+3),由① 得,![]() ,故动点R的轨迹方程为x2=4(y+3)(
,故动点R的轨迹方程为x2=4(y+3)(
![]() ).
).
18. [解析]:(1)由题意设过点M的切线方程为:![]() ,代入C得
,代入C得![]() ,
,
则![]() ,
,![]() ,即M(-1,
,即M(-1,![]() ).
).
(2)当a>0时,假设在C上存在点![]() 满足条件.设过Q的切线方程为:
满足条件.设过Q的切线方程为:![]() ,代入
,代入
![]()
![]() ,则
,则![]() ,
,
且![]()
![]() .若
.若![]() 时,由于
时,由于![]() ,
,
![]()
![]() ∴
∴ 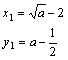 或
或 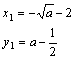 ;若k=0时,显然
;若k=0时,显然![]() 也满足要求.
也满足要求.
∴有三个点(-2+![]() ,
,![]() ),(-2-
),(-2-![]() ,
,![]() )及(-2,-
)及(-2,-![]() ),
),
且过这三点的法线过点P(-2,a),其方程分别为:
x+2![]() y+2-2a
y+2-2a![]() =0,x-2
=0,x-2![]() y+2+2a
y+2+2a![]() =0,x=-2.
=0,x=-2.
当a≤0时,在C上有一个点(-2,-![]() ),在这点的法线过点P(-2,a),其方程为:x=-2.
),在这点的法线过点P(-2,a),其方程为:x=-2.
§2.5圆锥曲线单元测试
1.D; 2.D; 3.D; 4.B; 5.A; 6.D; 7.D; 8.B;
9.C; 10.B; 11. C; 12.D; 13. ![]() 或
或![]() ;14.
;14. ![]() ;15.
;15. ![]() ;16.
;16. ![]() ;
;
17. 解:由已知条件得椭圆的焦点在x轴上,其中c=![]() ,a=3,从而b=1,所以其标准方程是:
,a=3,从而b=1,所以其标准方程是:
![]() .联立方程组
.联立方程组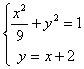 ,消去y得,
,消去y得, ![]() .
.
设A(![]() ),B(
),B(![]() ),AB线段的中点为M(
),AB线段的中点为M(![]() )那么:
)那么: ![]() ,
,![]() =
=![]()
所以![]() =
=![]() +2=
+2=![]() .
.
也就是说线段AB中点坐标为(-![]() ,
,![]() ).
).
18. 解:由于椭圆焦点为F(0,![]() 4),离心率为e=
4),离心率为e=![]() ,所以双曲线的焦点为F(0,
,所以双曲线的焦点为F(0,![]() 4),离心率为2,
4),离心率为2,
从而c=4,a=2,b=2![]() .
.
所以求双曲线方程为: ![]() .
.
19. 解:由于![]() ,PA=
,PA=![]()
=![]() =
=![]() ,其中x
,其中x![]()
(1)a![]() 1时,当且仅当x=0时,
1时,当且仅当x=0时, ![]() =PAmin=a.
=PAmin=a.
(2)a>时, 当且仅当x=a-1时, ![]() =PAmin=
=PAmin=![]() .
.
所以![]() =
=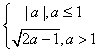 .
.
20. 解:设双曲线方程为x2-4y2=![]() .
.
联立方程组得: 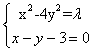 ,消去y得,3x2-24x+(36+
,消去y得,3x2-24x+(36+![]() )=0
)=0
设直线被双曲线截得的弦为AB,且A(![]() ),B(
),B(![]() ),那么:
),那么: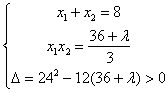
那么:AB=![]()
解得: ![]() =4,所以,所求双曲线方程是:
=4,所以,所求双曲线方程是:![]()
21. 解:(1)联立方程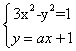 ,消去y得:(3-a2)x2-2ax-2=0.
,消去y得:(3-a2)x2-2ax-2=0.
设A(![]() ),B(
),B(![]() ),那么:
),那么: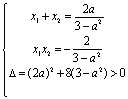
由于以AB线段为直径的圆经过原点,那么:![]() ,即
,即![]() 。
。
所以:![]() ,得到:
,得到:![]() ,解得a=
,解得a=![]()
(2)假定存在这样的a,使A(![]() ),B(
),B(![]() )关于直线
)关于直线![]() 对称。
对称。
那么: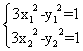 ,两式相减得:
,两式相减得:![]() ,从而
,从而![]()
因为A(![]() ),B(
),B(![]() )关于直线
)关于直线![]() 对称,所以
对称,所以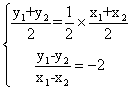
代入(*)式得到:-2=6,矛盾。
也就是说:不存在这样的a,使A(![]() ),B(
),B(![]() )关于直线
)关于直线![]() 对称。
对称。
第3章 导数及其运用
§3.1导数概念及其几何意义
经典例题:解:∵y=x,∴x>0时,y=x,则![]()
![]() ∴
∴![]()
![]() =1.
=1.
当x<0时,y=-x,![]() ,∴
,∴![]()
![]() .
.
∴y′=![]() .
.
当堂练习:
1.C; 2.D; 3.C; 4.A; 5.A; 6.B; 7.B; 8.B;
9.C; 10.B; 11.常数函数; 12.arctan![]() ; 13.(a+b)f′(x);
; 13.(a+b)f′(x);
14. 10 m/s;
15. 分析:Δs即位移的改变量,Δt即时间的改变量,![]() 即平均速度,当Δt越小,求出的
即平均速度,当Δt越小,求出的![]() 越接近某时刻的速度.
越接近某时刻的速度.
解:∵![]() =4t+2Δt
=4t+2Δt
∴(1)当t=2,Δt=0.01时,![]() =4×2+2×0.01=8.02
cm/s
=4×2+2×0.01=8.02
cm/s
(2)当t=2,Δt=0.001时,![]() =4×2+2×0.001=8.002
cm/s
=4×2+2×0.001=8.002
cm/s
(3)v=![]() (4t+2Δt)=4t=4×2=8 cm/s.
(4t+2Δt)=4t=4×2=8 cm/s.
16. 解:(1)k=![]()
![]() .∴点A处的切线的斜率为4.
.∴点A处的切线的斜率为4.
(2)点A处的切线方程是y-2=4(x-1)即y=4x-2
17. 解:![]()
![]() =
=![]()
![]() =
=![]() (Δx+1)=1
(Δx+1)=1
![]()
![]() =
=![]()
![]()
![]()
![]()
若b≠1,则![]()
![]() 不存在
不存在
∴b=1且a=1时,才有f(x)在x=0处可导
∴a=1,b=1.
18.解:f′(1)= ![]()
![]() =
= ![]()
![]()
=![]() =
=![]() .
.
§3.2导数的运算
经典例题:解:∵y'=![]() , y'x=0=1,∴tanθ=1,θ=
, y'x=0=1,∴tanθ=1,θ=![]() 为所求倾斜角.
为所求倾斜角.
当堂练习:
1.C; 2.C; 3.A; 4.D; 5.D; 6.D; 7.D; 8.B;
9.C; 10.C; 11. y=1; 12. 2sinx+xcosx;
13. cosx-xsinx+![]() ;14.
;14. ![]() ;
;
15. 解:∵y'=6x2-6x+6,∴y'x=1=6, y'x=-1=18. 设夹角为α, 则tanα=![]() =
=![]() ,
,
∴α=arctan![]() .
.
16. 解:∵f(x)=x3-x2,∴f'(x0)=3x02-2x0. 由f'(x0)=f(x0),得3x02-2x0=x03-x02,
即x03-4x02+2x0=0. 所以x0=0或x0=2±![]() .
.
17. 解:∵y'=(![]() )'=
)'=![]() =
=![]() ,∴y'x=1=-
,∴y'x=1=-![]() .
.
18. 解:∵y=![]() =
=![]() =
=![]() , ∴y'=
, ∴y'=![]() .
.
§3.3导数在研究函数中的应用
经典例题:解:(1) ![]()
由题意得: 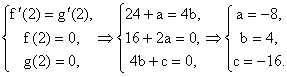
(2) 由(1)得![]()
![]()
![]() 由
由![]() 得:
得:![]() 或
或![]()
![]() 的递增区间是
的递增区间是![]() ;
; ![]() 的递减区间是
的递减区间是![]() .
.
当堂练习:
1.D; 2.B; 3.D; 4.B; 5.C; 6.A; 7.C; 8.C;
9.D; 10.C; 11. ![]() ; 12.
; 12. ![]() ; 13.
; 13. ![]() ;14.-3;
;14.-3;
15. 解: (1) ![]() 令
令![]() 或
或![]()
所以函数![]() 的单调递减区间为
的单调递减区间为![]() ,
, ![]() .
.
(2) 因为![]()
![]()
所以![]() . 因为在
. 因为在![]() 上
上![]() , 所以
, 所以![]() 在
在![]() 上单调递增, 又由于
上单调递增, 又由于
![]() 在
在![]() 上单调递减, 因此
上单调递减, 因此![]() 和
和![]() 分别是
分别是![]() 在区间
在区间![]() 上的最大值和
上的最大值和
最小值, 于是有![]() . 故
. 故![]()
因此![]() , 即函数
, 即函数![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
16. 解: (1) 由![]() 的图象经过P
的图象经过P![]() ,知
,知![]() , 所以
, 所以![]()
![]() .即
.即![]()
由在![]() 处的切线方程是
处的切线方程是![]() , 知
, 知
![]() ,
,![]()
故所求的解析式是 ![]()
(2) ![]() 令
令![]() 即
即![]()
解得 ![]() 当
当![]()
当![]()
故![]() 在
在![]() 内是增函数, 在
内是增函数, 在![]() 内是减函数,
内是减函数,
在![]() 内是增函数.
内是增函数.
17. 解: (1) ![]()
![]() 当
当![]() 时, y的极值为3.
时, y的极值为3.![]() .
.
(2) 令![]()
令![]() 或
或![]()
![]() y在
y在![]() 上为单调增函数;
上为单调增函数;
y在![]() 上为单调减函数.
上为单调减函数.
18. 解: ![]() 令
令![]() 得
得![]() 或
或![]() .
.
∵当![]() 或
或![]() 时,
时, ![]() ∴
∴![]() 在
在![]() 和
和![]() 上为增函数,
上为增函数,
在![]() 上为减函数, ∴
上为减函数, ∴![]() 在
在![]() 处有极大值, 在
处有极大值, 在![]() 处有极小值.
处有极小值.
极大值为![]() , 而
, 而![]() , ∴
, ∴![]() 在
在![]() 上的最大值为7.
上的最大值为7.
若对于任意x![]() 都有
都有![]() 成立, 得m的范围
成立, 得m的范围
![]() .
.
§3.4生活中的优化问题
经典例题: 分析 本题考查导数的应用及利用导数知识解决实际问题的能力.
解 由于瓶子的半径为r,所以每瓶饮料的利润是
y=f(r)=0.2×![]() πr3-0.8πr2=0.8π(
πr3-0.8πr2=0.8π(![]() -r2),0<r≤6.
-r2),0<r≤6.
令f′(r)=0.8π(r2-2r)=0.
当r=2时,f′(r)=0;
当r∈(0,2)时,f′(r)<0;
当r∈(2,6)时,f′(r)>0.
因此,当半径r>2时,f′(r)>0,它表示f(r)单调递增,即半径越大,利润越高;半径r<2时,f′(r)<0,它表示f(r)单调递减,即半径越大,利润越低.
(1)半径为6 cm时,利润最大.
(2)半径为2 cm时,利润最小,这时f(2)<0,表示此种瓶内饮料的利润还不够瓶子的成本,此时利润是负值.
当堂练习:
1.A; 2.A; 3.C; 4.C; 5.A; 6.D; 7.A; 8.A;
9.B; 10.D; 11. 7; 12.
(![]() ,+∞); 13. (0,
,+∞); 13. (0,![]() );14. 11;
);14. 11;
15. 解 ∵函数y=ax与y=-![]() 在区间(0,+∞)上是减函数,
在区间(0,+∞)上是减函数,
∴a<0,b<0.
由y=ax3+bx2+5,得y′=3ax2+2bx.
令y′>0,即3ax2+2bx>0,∴![]() <x<0.
<x<0.
因此当x∈(![]() ,0)时,函数为增函数;
,0)时,函数为增函数;
令y′<0,即3ax2+2bx<0,
∴x<![]() 或x>0.
或x>0.
因此当x∈(-∞,![]() )时,函数为减函数;
)时,函数为减函数;
x∈(0,+∞)时,函数也为减函数.
16. 分析 本题考查导数的几何意义及利用导数知识解决实际问题的能力.
解 (1)b′(t)=-2 000t+10 000,
b′(t)t=5=-2 000×5+10 000=0,
b′(t)t=10=-2 000×10+10 000=-10 000,
即细菌在t=5与t=10时的瞬时速度分别为0和-10 000.
(2)由-2 000t+10 000>0,得t<5,
由-2 000t+10 000<0,得t>5,
即细菌在t∈(0,5)时间段数量增加,在t∈(5,+∞)时间段数量减少.
17. 分析 本题主要考查函数、导数、不等式等基础知识,考查分析推理和知识的综合应用能力.求函数在闭区间的最值,只需比较导数为零的点与区间端点处的函数值的大小即可.
解 (1)由原式得f(x)=x3-ax2-4x+4a,
∴f′(x)=3x2-2ax-4.
(2)由f′(-1)=0,得a=![]() .
.
此时有f(x)=(x2-4)(x-![]() ),
),
∴f′(x)=3x2-x-4.
由f′(x)=0,得x=![]() 或x=-1.
或x=-1.
又f(![]() )=-
)=-![]() ,f(-1)=
,f(-1)=![]() ,f(-2)=0,f(2)=0,
,f(-2)=0,f(2)=0,
∴f(x)在[-2,2]上的最大值为![]() ,最小值为
,最小值为![]() .
.
18. 分析 在一定条件下,“利润最大”“用料最省”“面积最大”“效率最高”“强度最大”等问题,在生产、生活中经常用到,在数学上这类问题往往归结为求函数的最值问题.除了常见的求最值的方法外,还可用求导法求函数的最值.但无论采取何种方法都必须在函数的定义域内进行.
解法一 设相同的时间内,生产第x(x∈N*,1≤x≤10)档次的产品利润y最大.
依题意,得y=[8+2(x-1)][60-3(x-1)]
=-6x2+108x+378
=-6(x-9)2+864(1≤x≤10),
显然,当x=9时,ymax=864(元),
即在相同的时间内,生产第9档次的产品的总利润最大,最大利润为864元.
解法二 由上面解法得到y=-6x2+108x+378.
求导数,得y′=-12x+108.
令y′=-12x+108=0,
解得x=9.因为x=9∈[1,10],y只有一个极值点,所以它是最值点,即在相同的时间内,生产第9档次的产品利润最大,最大利润为864元.
§3.5导数及其运用单元测试
1.B; 2.D; 3.B; 4.D; 5.B; 6.C; 7.B; 8.A;
9.C; 10.D; 11. ![]() ; 12.
; 12.![]() ; 13.
; 13. ![]() ;14.
;14. ![]() ;
;
15、(I)解:![]()
令 ![]() 得
得![]()
若 ![]() 则
则![]() ,
,
故![]() 在
在![]() 上是增函数,
上是增函数,![]() 在
在![]() 上是增函数
上是增函数 ![]()
若 ![]() 则
则![]() ,故
,故![]() 在
在![]() 上是减函数
上是减函数 ![]()
(II)
![]()
![]()
![]()
![]()
16、解:(Ⅰ)当![]()
![]()
![]() ,化为
,化为![]()
![]()
![]()
故,满足(Ⅰ)条件的集合为![]()
![]()
(Ⅱ)![]()
要使f(x)在区间(0,+∞)上是单调减函数,必须![]() ,
,
即 ![]() ,但
,但![]() 时,
时,![]() 为常函数,所以
为常函数,所以![]()
17、.解:(I)![]()
(II)因![]()
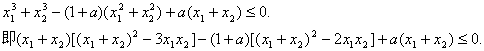
又由(I)知
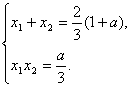 代入前面不等式,两边除以(1+a),并化简得
代入前面不等式,两边除以(1+a),并化简得
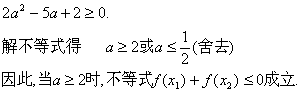
18、.解:(1)![]() 由条件知
由条件知
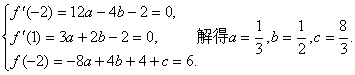
(2)![]()
| x | -3 | (-3,-2) | -2 | (-2,1) | 1 | (1,3) | 3 |
|
| + | 0 | - | 0 | + | ||
|
|
| ↗ | 6 | ↘ |
| ↗ |
|
由上表知,在区间[-3,3]上,当![]() 时,
时,![]()
![]() 时,
时,![]()
19、解:(Ⅰ)![]()
∴当![]() ,
,
∴![]() 的单调递增区间是
的单调递增区间是![]() ,单调递减区间是
,单调递减区间是![]()
当![]() ;当
;当![]()
(Ⅱ)由(Ⅰ)的分析可知![]() 图象的大致形状及走向(图略)
图象的大致形状及走向(图略)
∴当![]() 的图象有3个不同交点,
的图象有3个不同交点,
即方程![]() 有三解(
有三解(
(Ⅲ)![]()
∵![]() 上恒成立
上恒成立
令![]() ,由二次函数的性质,
,由二次函数的性质,![]() 上是增函数,
上是增函数,
∴![]() ∴所求k的取值范围是
∴所求k的取值范围是![]()
选修1-1综合测试
1.B; 2.C; 3.D; 4.A; 5.C; 6.B; 7.C; 8.A;
9.C; 10.A; 11. ![]() ; 12. 充分不必要; 13. (2);14.
; 12. 充分不必要; 13. (2);14. 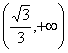
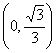 ;
;
15.

16(1)在![]()
![]() 上为单调递增区间,在
上为单调递增区间,在![]() 上为单调递减区间.
上为单调递减区间.
(2)x=1时,y=![]() ,x=
,x=![]() 时,y=
时,y=![]()
17.解:设P(x,y)是所求轨迹上的任一点,
①当斜率存在时,直线l的方程为y=kx+1,A(x1,y1),B(x2,y2),
由![]() 得:(4+k2)x2+2kx-3=0, x1+x2=-
得:(4+k2)x2+2kx-3=0, x1+x2=-![]() y1+y2=
y1+y2=![]() ,
,
由![]() 得:(x,y)=
得:(x,y)=![]() (x1+x2,y1+y2),
(x1+x2,y1+y2),
即: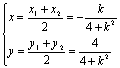
消去k得:4x2+y2-y=0
当斜率不存在时,AB的中点为坐标原点,也适合方程所以动点P的轨迹方程为:4x2+y2-y= 0。
18.
