![]() 选修1-2
第1章 统计案例
选修1-2
第1章 统计案例
§1.1独立性检验
重难点:了解独立性检验(只要求![]() 列联表)的基本思想、方法及其简单应用.
列联表)的基本思想、方法及其简单应用.
考纲要求:①了解独立性检验(只要求![]() 列联表)的基本思想、方法及其简单应用.
列联表)的基本思想、方法及其简单应用.
②了解假设检验的基本思想、方法及其简单应用.
经典例题:在一次恶劣气候的飞机航程中,调查了男女乘客在飞机上晕机的情况:男乘客晕机的有24人,不晕机的有31人;女乘客晕机的有8人,不晕机的有26人。请你根据所给数据判断是否在恶劣气候飞行中,男人比女人更容易晕机.
当堂练习:
1.独立性检验中的统计假设就是假设相关事件A,B ( )
A.互斥 B.不互斥 C.相互独立 D.不独立
2.下列说法中正确的是 ( )
①独立性检验的基本思想是带有概率性质的反证法;②独立性检验就是选取一个假设![]() 条件下的小概率事件,若在一次试验中该事件发生了,这是与实际推断相抵触的“不合理”现象,则作出拒绝
条件下的小概率事件,若在一次试验中该事件发生了,这是与实际推断相抵触的“不合理”现象,则作出拒绝![]() 的推断;③独立性检验一定能给出明确的结论.
的推断;③独立性检验一定能给出明确的结论.
A. ①② B.①③ C.②③ D.①②③
3.提出统计假设![]() ,计算出
,计算出![]() 的值,则拒绝
的值,则拒绝![]() 的是
(
)
的是
(
)
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4. 独立性检验中的“小概率事件”是指某事件发生的概率 ( )
A.小于4% B.小于5% C. 小于6% D.小于8%
5.给出假设![]() ,下列结论中不能对
,下列结论中不能对![]() 成立与否作出明确判断的是( )
成立与否作出明确判断的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
| 认为作业量大 | 认为作业量不大 | 总数 | |
| 男生 | 18 | 9 | 27 |
| 女生 | 8 | 15 | 23 |
| 总数 | 26 | 24 | 50 |
6.某班主任对全班50名学生进行了作业量的调查,数据如下表:
| 无效 | 有效 | 合计 | |
| 男性患者 | 15 | 35 | 50 |
| 女性患者 | 4 | 46 | 50 |
| 合计 | 19 | 81 | 100 |
则学生的性别与作业量的大小有关系的把握大约为( )
A.99% B.95%
C. 90% D.无充分根据
7.研究某新药的疗效,给50个患者服用此药,跟踪调查后得如右表的数据。
设![]() :服用此药的效果与患者的性别无关.则
:服用此药的效果与患者的性别无关.则![]() ,
,
从而得出结论
8.在性别与吃零食这两个分类变量的计算中,下列说法正确的是
①若![]() 的观测值为k=6.635,我们有99%的把握认为吃零食与性别有关系,那么在100个吃零食的人中必有99人是女性;
的观测值为k=6.635,我们有99%的把握认为吃零食与性别有关系,那么在100个吃零食的人中必有99人是女性;
②从独立性检验可知有99%的把握认为吃零食与性别有关系时,我们说某人吃零食,那么此人是女性的可能性为99%;
③若从统计量中求出有99%的把握认为吃零食与性别有关系,是指有1%的可能性使得出的判断出现错误.
9.下列关于![]() 的说法中,正确的是
的说法中,正确的是
①![]() 在任何相互独立问题中都可以用于检验是否相关;②
在任何相互独立问题中都可以用于检验是否相关;②![]() 越大,两个事件的相关性越大;③
越大,两个事件的相关性越大;③![]() 是用来判断两个相互独立事件相关与否的一个统计量,它可以用来判断两个事件是否相关这一类问题.
是用来判断两个相互独立事件相关与否的一个统计量,它可以用来判断两个事件是否相关这一类问题.
| 患肝病 | 未患肝病 | 合计 | |
| 酗酒 | 30 | 170 | 200 |
| 不酗酒 | 20 | 280 | 300 |
| 合计 | 50 | 450 | 500 |
10.某医疗机构为了了解肝病与酗酒是否有
关,对成年人进行了一次随机抽样调查,结果
如右表,则从直观上你能得到什么结论.
11.为了调查服用某种新药是否会患某种慢性病,调查了200名服用此新药和100名未服用此种新药的人,调查结果如下表,试问此种患慢性病是否与服用新药有关?
| 患慢性病 | 未患慢性病 | 合计 | |
| 服用新药 | 40 | 160 | 200 |
| 乙工作 | 13 | 87 | 100 |
| 合计 | 53 | 247 | 300 |
12.在对人们饮食习惯的一次调查中,共调查了124人,其中六十岁以上的70人,六十岁以下的54人,六十岁以上的人中有43人的饮食以蔬菜为主,另外27人则以肉类为主;六十岁以下的人中有21人饮食以蔬菜为主,另外33人则以肉类为主。(1)根据以上数据建立一个2×2的列联表;(2)判断人的饮食习惯是否与年龄有关.
![]() 选修1-2
第1章 统计案例
选修1-2
第1章 统计案例
§1.2回归分析
重难点:解聚类分析的基本思想、方法及其简单应用;了解回归的基本思想、方法及其简单应用.
考纲要求:①了解聚类分析的基本思想、方法及其简单应用.
②了解回归的基本思想、方法及其简单应用.
经典例题:某校医务室抽查了10名学生在高一和高二时的体重(单位:kg)如下表:
| 高一成绩 | 74 | 71 | 72 | 68 | 76 | 73 | 67 | 70 | 65 | 74 |
| 高二成绩 | 76 | 75 | 71 | 70 | 76 | 79 | 65 | 77 | 62 | 72 |
(1)利用相关系数r判断![]() 与
与![]() 是否具有相关关系?
是否具有相关关系?
(2)若![]() 与
与![]() 具有相关关系,试估计高一体重为78kg的学生在高二时的体重.
具有相关关系,试估计高一体重为78kg的学生在高二时的体重.
当堂练习:
1.下列两个变量之间的关系中,哪个是函数关系 ( )
A.学生的性别与他的数学成绩 B.人的工作环境与健康状况
C.女儿的身高与父亲的身高 D. 正三角形的边长与面积
2.从某大学随机选取8名女大学生,其身高![]() (cm)和体重
(cm)和体重![]() (kg)的回归方程为
(kg)的回归方程为 ![]() ,则身高172cm的女大学生,由回归方程可以预报其体重 ( )
,则身高172cm的女大学生,由回归方程可以预报其体重 ( )
A.为6 0.316![]() B. 约为6 0.316
B. 约为6 0.316![]() C.大于6 0.316
C.大于6 0.316![]() D.小于6 0.316
D.小于6 0.316![]()
3.为研究变量![]() 和
和![]() 的线性相关性,甲、乙二人分别作了研究,利用线性回归方法得到回归直线方程
的线性相关性,甲、乙二人分别作了研究,利用线性回归方法得到回归直线方程![]() 和
和![]() ,两人计算知
,两人计算知![]() 相同,
相同,![]() 也相同,则
也相同,则![]() 与
与![]() 的关系为 ( )
的关系为 ( )
A.重合 B.平行 C.相交于点![]() D. 无法判断
D. 无法判断
4.设两个变量x和y之间具有线性相关关系,它们的相关系数是![]() ,
,![]() 关于
关于![]() 的回归直线的回归系数为
的回归直线的回归系数为![]() ,回归截距是
,回归截距是![]() ,那么必有
(
)
,那么必有
(
)
A.![]() 与
与![]() 的符号相同 B.
的符号相同 B. ![]() 与
与![]() 的符号相同 C.
的符号相同 C. ![]() 与
与![]() 的符号相反 D.
的符号相反 D. ![]() 与
与![]() 的符号相反
的符号相反
5. 工人月工资(元)依劳动生产率(千元)变化的回归直线方程为![]() ,下列判断正确的是
(
)
,下列判断正确的是
(
)
A.劳动生产率为1000元时,工资为340元
B.劳动生产率提高1000元时,工资提高180元
C.劳动生产率提高1000元时,工资平均提高180元
D.工资为520元时,劳动生产率为2000元
6.由右表可计算出变量![]() 的线性回归方程为( )
的线性回归方程为( )
|
| 5 | 4 | 3 | 2 | 1 |
|
| 2 | 1.5 | 1 | 1 | 0.5 |
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
7.若回归直线方程中的回归系数b=0时,则相关系数![]() =
=
8.下列结论中,能表示变量![]() 具有线性相关关系的是
具有线性相关关系的是
①![]() ②
②![]() ③
③![]() ④
④![]()
9.下列说法中正确的是 (填序号)
①回归分析就是研究两个相关事件的独立性;②回归模型都是确定性的函数;③回归模型都是线性的;④回归分析的第一步是画散点图或求相关系数![]() ;⑤回归分析就是通过分析、判断,确定相关变量之间的内在的关系的一种统计方法.
;⑤回归分析就是通过分析、判断,确定相关变量之间的内在的关系的一种统计方法.
10.变量![]() 与
与![]() 具有线性相关关系,当
具有线性相关关系,当![]() 取值为16,14,12,8时,通过观测得到
取值为16,14,12,8时,通过观测得到![]() 的值分别为11,9,8,5.若在实际问题中,
的值分别为11,9,8,5.若在实际问题中,![]() 的预报最大取值是10,则
的预报最大取值是10,则![]() 的最大取值不能超过多少?
的最大取值不能超过多少?
11.在某年一项关于16艘轮船的研究中,船的吨位区间从192吨到3246吨,船员的数目从5人到32人.船员人数![]() 关于船的吨位
关于船的吨位![]() 的线性回归方程为
的线性回归方程为![]()
(1)假设两艘轮船吨位相差1000吨,则船员平均人数相差多少?
(2)对于最小的船估计的船员数是多少?对于最大的船估计的船员数是多少?(本小题保留整数)
12.已知10只狗的血球体积及红血球的测量值如下(x(血球体积,mm),y(血红球数,百万)):
| x | 45 | 42 | 46 | 48 | 42 | 35 | 58 | 40 | 39 | 50 |
| y | 6.53 | 6.30 | 9.25 | 7.50 | 6.99 | 5.90 | 9.49 | 6.20 | 6.55 | 7.72 |
(1)画出上表的散点图; (2)求![]() ,
,![]() ,
,![]() ,
,![]() ; (3)由散点图判断能否用线性回归方程来刻画
; (3)由散点图判断能否用线性回归方程来刻画![]() 与
与![]() 之间的关系,若能,求出线性回归方程.
之间的关系,若能,求出线性回归方程.
![]() 选修1-2
第1章 统计案例
选修1-2
第1章 统计案例
§1.3统计案例单元测试
参考公式
|
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
|
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
1、 在画两个变量的散点图时,下面哪个叙述是正确的( )
(A)预报变量在![]() 轴上,解释变量在
轴上,解释变量在![]() 轴上
轴上
(B)解释变量在![]() 轴上,预报变量在
轴上,预报变量在![]() 轴上
轴上
(C)可以选择两个变量中任意一个变量在![]() 轴上
轴上
(D)可以选择两个变量中任意一个变量在![]() 轴上
轴上
2、设两个变量x和y之间具有线性相关关系,它们的相关系数是r,y关于x的回归直线的斜率是b,纵截距是a,那么必有( )
(A) b与r的符号相同 (B) a与r的符号相同
(C) b与r的相反 (D) a与r的符号相反
3、一位母亲记录了儿子3~9岁的身高,由此建立的身高与年龄的回归模型为y=7.19x+73.93
用这个模型预测这个孩子10岁时的身高,则正确的叙述是( )
(A)身高一定是145.83cm (B)身高在145.83cm以上
(C)身高在145.83cm以下 (D)身高在145.83cm左右
4、两个变量![]() 与
与![]() 的回归模型中,分别选择了4个不同模型,它们的相关指数
的回归模型中,分别选择了4个不同模型,它们的相关指数![]() 如下 ,其中拟合效果最好的模型是( )
如下 ,其中拟合效果最好的模型是( )
(A)模型1的相关指数![]() 为0.98 (B) 模型2的相关指数
为0.98 (B) 模型2的相关指数![]() 为0.80
为0.80
(C)模型3的相关指数![]() 为0.50 (D) 模型4的相关指数
为0.50 (D) 模型4的相关指数![]() 为0.25
为0.25
5、工人月工资(元)依劳动生产率(千元)变化的回归直线方程为![]() ,下列判断正确的是( )
,下列判断正确的是( )
(A)劳动生产率为1000元时,工资为50元
(B)劳动生产率提高1000元时,工资提高150元
(C)劳动生产率提高1000元时,工资提高90元
(D)劳动生产率为1000元时,工资为90元
6、为研究变量![]() 和
和![]() 的线性相关性,甲、乙二人分别作了研究,利用线性回归方法得到回归直线方程
的线性相关性,甲、乙二人分别作了研究,利用线性回归方法得到回归直线方程![]() 和
和![]() ,两人计算知
,两人计算知![]() 相同,
相同,![]() 也相同,下列正确的是( )
也相同,下列正确的是( )
(A) ![]() 与
与![]() 重合
(B)
重合
(B) ![]() 与
与![]() 一定平行
一定平行
(C) ![]() 与
与![]() 相交于点
相交于点![]() (D) 无法判断
(D) 无法判断![]() 和
和![]() 是否相交
是否相交
7、考察棉花种子经过处理跟生病之间的关系得到如下表数据:
| 种子处理 | 种子未处理 | 合计 | |
| 得病 | 32 | 101 | 133 |
| 不得病 | 61 | 213 | 274 |
| 合计 | 93 | 314 | 407 |
根据以上数据,则( )
(A)种子经过处理跟是否生病有关 (B)种子经过处理跟是否生病无关
(C)种子是否经过处理决定是否生病 (D)以上都是错误的
8、变量![]() 与
与![]() 具有线性相关关系,当
具有线性相关关系,当![]() 取值16,14,12,8时,通过观测得到
取值16,14,12,8时,通过观测得到![]() 的值分别为11,9,8,5,若在实际问题中,
的值分别为11,9,8,5,若在实际问题中,![]() 的预报最大取值是10,则
的预报最大取值是10,则![]() 的最大取值不能超过( )
的最大取值不能超过( )
(A)16 (B)17 (C)15 (D)12
9、在研究身高和体重的关系时,求得相关指数![]() ______________,可以叙述为“身高解释了64%的体重变化,而随机误差贡献了剩余的36%”所以身高对体重的效应比随机误差的效应大得多。
______________,可以叙述为“身高解释了64%的体重变化,而随机误差贡献了剩余的36%”所以身高对体重的效应比随机误差的效应大得多。
10、某大学在研究性别与职称(分正教授、副教授)之间是否有关系,你认为应该收集哪些数据?
11、某高校“统计初步”课程的教师随机调查了选该课的一些学生情况,具体数据如下表:
| 性别 专业 | 非统计专业 | 统计专业 |
| 男 | 13 | 10 |
| 女 | 7 | 20 |
为了判断主修统计专业是否与性别有关系,根据表中的数据,得到
![]()
因为![]() ,所以判定主修统计专业与性别有关系,那么这种判断出错的可能性为_____________
,所以判定主修统计专业与性别有关系,那么这种判断出错的可能性为_____________
12、许多因素都会影响贫穷,教育也许是其中之一,在研究这两个因素的关系时收集了美国50个州的成年人受过9年或更少教育的百分比(![]() )和收入低于官方规定的贫困线的人数占本州人数的百分比(
)和收入低于官方规定的贫困线的人数占本州人数的百分比(![]() )的数据,建立的回归直线方程如下
)的数据,建立的回归直线方程如下![]() ,斜率的估计等于0.8说明
,成年人受过9年或更少教育的百分比(
,斜率的估计等于0.8说明
,成年人受过9年或更少教育的百分比(![]() )和收入低于官方的贫困线的人数占本州人数的百分比(
)和收入低于官方的贫困线的人数占本州人数的百分比(![]() )之间的相关系数
(填充“大于0”或“小于0”)
)之间的相关系数
(填充“大于0”或“小于0”)
13、在对人们的休闲方式的一次调查中,共调查了124人,其中女性70人,男性54人。女性中有43人主要的休闲方式是看电视,另外27人主要的休闲方式是运动;男性中有21人主要的休闲方式是看电视,另外33人主要的休闲方式是运动。
(1)根据以上数据建立一个2×2的列联表;
(2)判断性别与休闲方式是否有关系。
14、某种书每册的成本费y(元)与印刷册数x(千册)有关,经统计得到数据如下:
| x | 1 | 2 | 3 | 5 | 10 | 20 | 30 | 50 | 100 | 200 |
| y | 10.15 | 5.52 | 4.08 | 2.85 | 2.11 | 1.62 | 1.41 | 1.30 | 1.21 | 1.15 |
检验每册书的成本费y与印刷册数的倒数![]() 之间是否具有线性相关关系,如有,求出y对x的回归方程。
之间是否具有线性相关关系,如有,求出y对x的回归方程。
![]() 选修1-2
第2章 推理与证明
选修1-2
第2章 推理与证明
§2.1-2 合情推理与演绎推理、直接证明与间接证明
重难点:了解合情推理的含义,能利用归纳和类比等进行简单的推理,了解合情推理在数学发现中的作用;了解演绎推理的重要性,掌握演绎推理的基本模式,并能运用它们进行一些简单推理;了解合情推理和演绎推理之间的联系和差异;了解直接证明的两种基本方法:分析法和综合法;了解分析法和综合法的思考过程、特点;了解间接证明的一种基本方法――反证法;了解反证法的思考过程、特点.
考纲要求:①了解合情推理的含义,能利用归纳和类比等进行简单的推理,了解合情推理在数学发现中的作用.
②了解演绎推理的重要性,掌握演绎推理的基本模式,并能运用它们进行一些简单推理.
③了解合情推理和演绎推理之间的联系和差异.
④了解直接证明的两种基本方法:分析法和综合法;了解分析法和综合法的思考过程、特点.
⑤了解间接证明的一种基本方法――反证法;了解反证法的思考过程、特点.
经典例题:25. 通过计算可得下列等式:
![]()
![]()
![]()
┅┅
![]()
将以上各式分别相加得:![]()
即:![]()
类比上述求法:请你求出![]() 的值..
的值..
当堂练习:
1.如果数列![]() 是等差数列,则( )
是等差数列,则( )
A.![]() B.
B.
![]() C.
C.![]() D.
D.![]()
2.下面使用类比推理正确的是 ( )
A.“若![]() ,则
,则![]() ”类推出“若
”类推出“若![]() ,则
,则![]() ”
”
B.“若![]() ”类推出“
”类推出“![]() ”
”
C.“若![]() ” 类推出“
” 类推出“![]() (c≠0)”
(c≠0)”
D.“![]() ” 类推出“
” 类推出“![]() ”
”
3.有这样一段演绎推理是这样的“有些有理数是真分数,整数是有理数,则整数是真分数”
结论显然是错误的,是因为 ( )
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
4.设![]() ,
,![]()
![]() ,n∈N,则
,n∈N,则![]() ( )
( )
A.![]() B.-
B.-![]() C.
C.![]() D.-
D.-![]()
5.在十进制中![]() ,那么在5进制中数码2004折合成十进制为(
)
,那么在5进制中数码2004折合成十进制为(
)
A.29 B. 254 C. 602 D. 2004
6.函数![]() 的图像与直线
的图像与直线![]() 相切,则
相切,则![]() =( )
=( )
A. ![]() B.
B.![]() C.
C.
![]() D. 1
D. 1
7.下面的四个不等式:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中不成立的有 ( )
.其中不成立的有 ( )
A.1个 B.2个 C.3个 D.4个
8.抛物线![]() 上一点
上一点![]() 的纵坐标为4,则点
的纵坐标为4,则点![]() 与抛物线焦点的距离为( )
与抛物线焦点的距离为( )
A.2 B.3 C.4 D. 5
9.设 ![]() , 则
, 则![]() ( )
( )
A. ![]() B.
0 C.
B.
0 C.![]() D. 1
D. 1
10.已知向量![]() ,
, ![]() ,且
,且![]() , 则由
, 则由![]() 的值构成的集合是( )
的值构成的集合是( )
A.{2,3} B. {-1, 6} C. {2} D. {6}
11. 有一段演绎推理是这样的:“直线平行于平面,则平行于平面内所有直线;已知直线![]() 平面
平面![]() ,直线
,直线![]() 平面
平面![]() ,直线
,直线![]() ∥平面
∥平面![]() ,则直线
,则直线![]() ∥直线
∥直线![]() ”的结论显然是错误的,这是因为( )
”的结论显然是错误的,这是因为( )
A.大前提错误 B.小前提错误 C.推理形式错误 D.非以上错误
12.已知![]()
![]() ,猜想
,猜想![]() 的表达式为( )
的表达式为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
13. 类比平面几何中的勾股定理:若直角三角形ABC中的两边AB、AC互相垂直,则三角形三边长之间满足关系:![]() 。若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则三棱锥的侧面积与底面积之间满足的关系为
.
。若三棱锥A-BCD的三个侧面ABC、ACD、ADB两两互相垂直,则三棱锥的侧面积与底面积之间满足的关系为
.
14.从![]() 中,可得到一般规律为 (用数学表达式表示)
中,可得到一般规律为 (用数学表达式表示)
15.函数y=f(x)在(0,2)上是增函数,函数y=f(x+2)是偶函数,则f(1),f(2.5),f(3.5)的大小关系是 .
16.设平面内有n条直线![]() ,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用
,其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用![]() 表示这n条直线交点的个数,则
表示这n条直线交点的个数,则![]() =
;当n>4时,
=
;当n>4时,![]() =
(用含n的数学表达式表示)
=
(用含n的数学表达式表示)
17.证明:![]() 不能为同一等差数列的三项.
不能为同一等差数列的三项.
18.在△ABC中,![]() ,判断△ABC的形状.
,判断△ABC的形状.
19.已知:空间四边形ABCD中,E,F分别为BC,CD的中点,判断直线EF与平面ABD的关系,并证明你的结论.
20.已知函数![]() ,求
,求![]() 的最大值.
的最大值.
21.△ABC三边长![]() 的倒数成等差数列,求证:角
的倒数成等差数列,求证:角![]()
![]() .
.
22.在各项为正的数列![]() 中,数列的前n项和
中,数列的前n项和![]() 满足
满足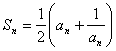
(1) 求![]() ;(2) 由(1)猜想数列
;(2) 由(1)猜想数列![]() 的通项公式;(3) 求
的通项公式;(3) 求![]()
23.自然状态下鱼类是一种可再生资源,为持续利用这一资源,需从宏观上考察其再生能力及捕捞强度对鱼群总量的影响,用![]() 表示某鱼群在第
表示某鱼群在第![]() 年年初的总量,
年年初的总量,![]() ,且
,且![]() >0.不考虑其它因素,设在第
>0.不考虑其它因素,设在第![]() 年内鱼群的繁殖量及捕捞量都与
年内鱼群的繁殖量及捕捞量都与![]() 成正比,死亡量与
成正比,死亡量与![]() 成正比,这些比例系数依次为正常数
成正比,这些比例系数依次为正常数![]() .
.
(Ⅰ)求![]() 与
与![]() 的关系式;
的关系式;
(Ⅱ)猜测:当且仅当![]() ,
,![]() 满足什么条件时,每年年初鱼群的总量保持不变?(不要求证明)
满足什么条件时,每年年初鱼群的总量保持不变?(不要求证明)
24. 设函数![]() .
.
(1)证明:![]() ;
;
(2)设![]() 为
为![]() 的一个极值点,证明
的一个极值点,证明![]() .
.
25.已知![]() 恒不为0,对于任意
恒不为0,对于任意![]()
等式![]() 恒成立.求证:
恒成立.求证:![]() 是偶函数.
是偶函数.
26.已知ΔABC的三条边分别为![]() 求证:
求证:![]()
![]() 选修1-2
第2章 推理与证明
选修1-2
第2章 推理与证明
§2.3 推理与证明单元测试
1、由数列1,10,100,1000,……猜测该数列的第n项可能是( )
A.10n; B.10n-1; C.10n+1; D.11n.
2、类比平面内正三角形的“三边相等,三内角相等”的性质,可推出正四面体的下列哪些性质,你认为比较恰当的是( )
①各棱长相等,同一顶点上的任两条棱的夹角都相等;②各个面都是全等的正三角形,相邻两个面所成的二面角都相等;③各个面都是全等的正三角形,同一顶点上的任两条棱的夹角都相等
A.①; B.①②; C.①②③; D.③。
3、下列表述正确的是( )
①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理。
A.①②③; B.②③④; C.②④⑤; D.①③⑤。
4、演绎推理是以下列哪个为前提,推出某个特殊情况下的结论的推理方法( )
A.一般的原理原则; B.特定的命题; C.一般的命题; D.定理、公式。
5、实数a、b、c不全为0的条件是( )
A.a、b、c均不为0; B.a、b、c中至少有一个为0;
C.a、b、c至多有一个为0; D.a、b、c至少有一个不为0。
6、设m≠n,x=m4-m3n,y=n3m-n4,则x与y的大小关系为( )
A.x>y; B.x=y; C.x<y; D.x≠y。
7、下列表述:①综合法是执因导果法;②综合法是顺推法;③分析法是执果索因法;④分析法是间接证法;⑤反证法是逆推法。正确的语句有( )个
A.2; B.3; C.4; D.5。
8、在演绎推理中,只要 是正确的,结论必定是正确的。
9、用演绎法证明y=x2是增函数时的大前提是 。
10、由“等腰三角形的两腰相等”可以类比推出正棱锥的类似属性是 。
11、如果数列{an}的前n项和Sn=2n2-3n,那么这个数列是 数列。
12、命题“△ABC中,若∠A>∠B,则a>b”的结论的否定是 。
13、在数列{an}中,![]() ,试猜想这个数列的通项公式。
,试猜想这个数列的通项公式。
14、用适当方法证明:已知:![]() ,求证:
,求证:![]() 。
。
![]() 选修1-2
第3章 数系的扩充与复数的引入
选修1-2
第3章 数系的扩充与复数的引入
§3.1复数的概念
重难点:理解复数的基本概念;理解复数相等的充要条件;了解复数的代数表示法及其几何意义.
考纲要求:①理解复数的基本概念.
②理解复数相等的充要条件.
③了解复数的代数表示法及其几何意义.
经典例题: 若复数![]() ,求实数
,求实数![]() 使
使![]() 。(其中
。(其中![]() 为
为![]() 的共轭复数).
的共轭复数).
当堂练习:
1.![]() 是复数
是复数![]() 为纯虚数的( )
为纯虚数的( )
A.充分条件 B.必要条件 C.充要条件 D.非充分非必要条件
2.设![]() ,则
,则![]() 在复平面内对应的点位于( )
在复平面内对应的点位于( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.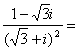 ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.复数z满足![]() ,那么
,那么![]() =( )
=( )
A.2+i B.2-i C.1+2i D.1-2i
5.如果复数![]() 的实部与虚部互为相反数,那么实数b等于( )
的实部与虚部互为相反数,那么实数b等于( )
A. B. C.2 D.-
6.集合{Z︱Z=![]() },用列举法表示该集合,这个集合是( )
},用列举法表示该集合,这个集合是( )
A{0,2,-2} B.{0,2}
C.{0,2,-2,2![]() }
D.{0,2,-2,2
}
D.{0,2,-2,2![]() ,-2
,-2![]() }
}
7.设O是原点,向量![]() 对应的复数分别为
对应的复数分别为![]() ,那么向量
,那么向量![]() 对应的复数是( )
对应的复数是( )
![]()
![]()
![]()
![]()
8、复数![]() ,则
,则![]() 在复平面内的点位于第( )象限。
在复平面内的点位于第( )象限。
A.一 B.二 C.三 D .四
9.复数![]() 不是纯虚数,则有( )
不是纯虚数,则有( )
![]()
![]()
![]()
![]()
10.设i为虚数单位,则![]() 的值为( )
的值为( )
A.4 B.-4 C.4i D.-4i
11.设![]() (
(![]() 为虚数单位),则z=
;z=
.
为虚数单位),则z=
;z=
.
12.复数![]() 的实部为 ,虚部为
。
的实部为 ,虚部为
。
13.已知复数z与 (z +2)2-8i 均是纯虚数,则 z =
14.设![]() ,
,![]() ,复数
,复数![]() 和
和![]() 在复平面内对应点分别为A、B,O为原点,则
在复平面内对应点分别为A、B,O为原点,则![]() 的面积为
。
的面积为
。
15. 已知复数z=(2+![]() )
)![]()
![]()
![]() ).当实数m取什么值时,复数z是:
).当实数m取什么值时,复数z是:
(1)零;(2)虚数;(3)纯虚数;(4)复平面内第二、四象限角平分线上的点对应的复数。
![]()
17. 设![]() R,若z对应的点在直线
R,若z对应的点在直线![]() 上。求m的值。
上。求m的值。
18. 已知关于![]() 的方程组
的方程组![]() 有实数,求
有实数,求![]() 的值。
的值。
.
![]() 选修1-2
第3章 数系的扩充与复数的引入
选修1-2
第3章 数系的扩充与复数的引入
§3.2-3复数的四则运算及几何意义
重难点:会进行复数代数形式的四则运算;了解复数代数形式的加、减运算的几何意义.
考纲要求:①会进行复数代数形式的四则运算.
②了解复数代数形式的加、减运算的几何意义.
经典例题:已知关于x的方程![]() 有实根,求这个实根以及实数k的值.
有实根,求这个实根以及实数k的值.
当堂练习:
1、对于![]() ,下列结论成立的是
( )
,下列结论成立的是
( )
A ![]() 是零
B
是零
B ![]() 是纯虚数 C
是纯虚数 C ![]() 是正实数 D
是正实数 D ![]() 是负实数
是负实数
2、已知![]() ,那么复数
,那么复数![]() 在复平面内对应的点位于
(
)
在复平面内对应的点位于
(
)
A 第一象限 B 第二象限 C 第三象限 D 第四象限
3、设非零复数x,y满足![]() ,则代数式
,则代数式![]() 的值是 ( )
的值是 ( )
A![]() B -1 C 1
D 0
B -1 C 1
D 0
4、若![]() ,则z的最大值是 ( )
,则z的最大值是 ( )
A 3 B 7 C 9 D 5
5、复数z在复平面内对应的点为A,将点A绕坐标原点按逆时针方向旋转![]() ,再向左平移一个单位,向下平移一个单位,得到点B,此时点B与点A恰好关于坐标原点对称,则复数z为
(
)
,再向左平移一个单位,向下平移一个单位,得到点B,此时点B与点A恰好关于坐标原点对称,则复数z为
(
)
A -1 B 1 C i D-i
6、![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、复数z=i+i2+i3+i4的值是 ( )
A.-1 B.0 C.1 D.i
8.设复平面内,向量![]() 的复数是1+i,将向量
的复数是1+i,将向量![]() 向右平移一个单位后得到向量
向右平移一个单位后得到向量![]() ,则向量
,则向量![]() 与点A′对应的复数分别是c
与点A′对应的复数分别是c
A.1+i与1+i B.2+i与2+i
C.1+i与2+i D.2+i与1+i
9.若复数z满足z+i+z-i=2,则z+i+1的最小值是a
A.1 B.![]() C.2 D.
C.2 D.![]()
10.若集合A={zz-1≤1,z∈C},B={zargz≥![]() ,z∈C},则集合A∩B在复平面内所表示的图形的面积是b
,z∈C},则集合A∩B在复平面内所表示的图形的面积是b
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.已知![]() .求
.求![]() 的值 .
的值 .
12.已知复数![]() .
.
13.复平面内点A对应的复数为2+i,点B对应的复数为3+3i,向量![]() 绕点A逆时针旋转90°到
绕点A逆时针旋转90°到![]() ,则点C对应的复数为_________.
,则点C对应的复数为_________.
14.设复数z=cosθ+(2-sin2θ)i.当θ∈(-![]() )时,复数z在复平面内对应点的轨迹方程是_________.
)时,复数z在复平面内对应点的轨迹方程是_________.
15. 已知![]() ,且复数
,且复数![]() 的虚部减去它的实部所得的差等于
的虚部减去它的实部所得的差等于![]() ,求复数
,求复数![]() 的模.
的模.
16. 已知复数![]() 当
当![]() 求a的取值范围,
求a的取值范围,![]()
17. 在复数范围内解方程![]() (i为虚数单位)
(i为虚数单位)
18. 复平面内点A对应的复数是1,过点A作虚轴的平行线l,设l上的点对应的复数为z,求![]() 所对应的点的轨迹.
所对应的点的轨迹.
![]() 选修1-2
第3章 数系的扩充与复数的引入
选修1-2
第3章 数系的扩充与复数的引入
§3.4 数系的扩充与复数的引入单元测试
1、复数![]() 的值等于( )
的值等于( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
2、已知集合M={1,![]() },N={1,3},M∩N={1,3},则实数m的值为( )
},N={1,3},M∩N={1,3},则实数m的值为( )
(A) 4 (B)-1 (C)4或-1 (D)1或6
3、设复数![]() 则
则![]() 是
是![]() 是纯虚数的( )
是纯虚数的( )
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分又不必要条件
4、复数Z与点Z对应,![]() 为两个给定的复数,
为两个给定的复数,![]() ,则
,则![]() 决定的Z的轨迹是( )
决定的Z的轨迹是( )
(A)过![]() 的直线
(B)线段
的直线
(B)线段![]() 的中垂线
的中垂线
(C)双曲线的一支
(D)以Z![]() 为端点的圆
为端点的圆
5、设复数![]() 满足条件
满足条件![]() 那么
那么![]() 的最大值是( )
的最大值是( )
(A)3 (B)4
(C)![]() (D)
(D)![]()
6、复平面上的正方形的三个顶点表示的复数有三个为![]() 那么第四
那么第四
个顶点对应的复数是( )
(A)![]() (B)
(B)![]() (C)
(C)![]() (D)
(D)![]()
7、集合{Z︱Z=![]() },用列举法表示该集合,这个集合是( )
},用列举法表示该集合,这个集合是( )
A{0,2,-2} (B){0,2} (C){0,2,-2,2![]() }(D){0,2,-2,2
}(D){0,2,-2,2![]() ,-2
,-2![]() }
}
8、![]()
![]() 则
则![]() (
)
(
)
(A)![]() (B)
(B)![]() (C)2
(D)2
(C)2
(D)2![]()
9、对于两个复数![]() ,
,![]() ,有下列四个结论:①
,有下列四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,其中正确的结论的个数为( )
,其中正确的结论的个数为( )
(A)1 (B)2 (C)3 (D)4
10、1,![]() ,
,![]() 是某等比数列的连续三项,则
是某等比数列的连续三项,则![]() 的值分别为( )
的值分别为( )
(A)![]() (B)
(B)![]()
(C)![]() (D)
(D)![]()
11、计算:![]() =
=
12、已知复数z1=3+4i, z2=t+i,,且z1·![]() 是实数,则实数t等于
是实数,则实数t等于
13、如果复数![]() 满足
满足![]() ,则
,则![]() 的最大值是
的最大值是
14、已知虚数![]() (
(![]() )的模为
)的模为![]() ,则
,则![]() 的最大值是 ,
的最大值是 ,![]() 的最小值为 .
的最小值为 .
15、设复数![]() ,试求m取何值时
,试求m取何值时
(1)Z是实数; (2)Z是纯虚数; (3)Z对应的点位于复平面的第一象限
16、在复数范围内解方程![]() (i为虚数单位)
(i为虚数单位)
17、设![]() 满足下列条件的复数
满足下列条件的复数![]() 所对应的点
所对应的点![]() 的集合表示什么图形
的集合表示什么图形
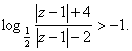
18、已知复数![]() ,
,![]() 满足
满足![]() ,且
,且![]() 为纯虚数,求证:
为纯虚数,求证:![]() 为实数
为实数
19、已知![]() ,
,![]() 对于任意实数x,都有
对于任意实数x,都有![]() 恒成立,试求实数
恒成立,试求实数![]() 的取值范围
的取值范围
20、设关于![]() 的方程
的方程![]() ,若方程有实数根,求锐角
,若方程有实数根,求锐角![]() 和实数根
和实数根
![]() 选修1-2
第4章 框图
选修1-2
第4章 框图
§4.1-2流程图、结构图
重难点:了解工序流程图(即统筹图)和结构图;能绘制简单实际问题的流程图,了解流程图在解决实际问题中的作用;会运用结构图梳理已学过的知识、整理收集到的资料信息.
考纲要求:①了解程序框图.
②了解工序流程图(即统筹图)和结构图.
③能绘制简单实际问题的流程图,了解流程图在解决实际问题中的作用;会运用结构图梳理已学过的知识、整理收集到的资料信息.
经典例题:画出解关于![]() 的不等式,
的不等式,![]() (
(![]() )的流程图.
)的流程图.
当堂练习:
1.下列流程图的基本符号中,表示判断的是( )
![]()
![]()
![]()
![]() A.
B.
C.
D.
A.
B.
C.
D.
2.下列的流程图示中表示选择结构的是( )
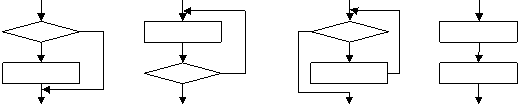

A. B. C. D.
3.下列对程序框图的描述,正确的是( )
A.只有一个起点,一个终点 B.只有一个起点,一个或多个终点
C.多个起点,一个或多个终点 D.多个起点,只有一个终点
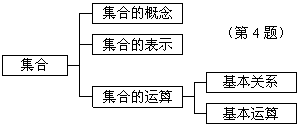 4.右图是《集合》的知识结构图,如果要加入“子集”,则应该放在( )
4.右图是《集合》的知识结构图,如果要加入“子集”,则应该放在( )
A.“集合的概念”的下位
B.“集合的表示”的下位
C.“基本关系”的下位
D.“基本运算”的下位
5.下面的程序框图的作用是按大小顺序输出两数,则括号处的处理可以是( )


A.A←B:B←A B.T←B:B←A :A←T C. T←B:A←T :B←A D.A←B:T←A :B←T
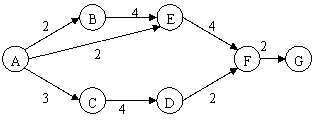 6.某成品的组装工序图如右,箭头上的数字表示组装过程中所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工作,则组装该产品所需要的最短时间是( )
6.某成品的组装工序图如右,箭头上的数字表示组装过程中所需要的时间(小时),不同车间可同时工作,同一车间不能同时做两种或两种以上的工作,则组装该产品所需要的最短时间是( )
A.11 B.13 C.15 D.17
7.一般来说,一个复杂的流程图都可以分解成_________、_________、__________三种结构;
8.一般地,对于树状结构图,下位比上位________,上位比下位___________;
9.读下面的流程图,若输入的值为-5时,输出的结果是__________.
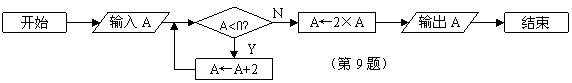
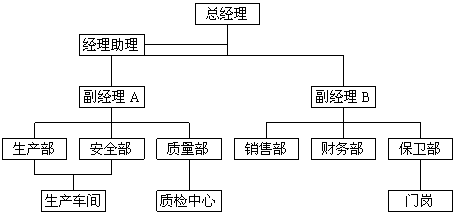
 10.某公司做人事调整:设总经理一个,配有经理助理一名;设副经理两人,直接对总经理负责,设有6个部门,其中副经理A管理生产部、安全部和质量部,经理B管理销售部、财务部和保卫部;生产车间由生产部和安全部共同管理,公司配有质检中心和门岗。请根据以上信息设计并画出该公司的人事结构图。
10.某公司做人事调整:设总经理一个,配有经理助理一名;设副经理两人,直接对总经理负责,设有6个部门,其中副经理A管理生产部、安全部和质量部,经理B管理销售部、财务部和保卫部;生产车间由生产部和安全部共同管理,公司配有质检中心和门岗。请根据以上信息设计并画出该公司的人事结构图。
11.观察下面的过程,回答问题:
因为![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ,
,
所以![]()
(1)上面的计算求的是什么?
(2)根据上面的例子归纳出算法,并画出流程图。
![]() 选修1-2
选修1-2综合测试
选修1-2
选修1-2综合测试
1.复数-9的平方根是 ( )
A.![]() B.
B.![]() C.
C.![]() D.不存在
D.不存在
2.已知复数z满足![]() ,则z等于( )
,则z等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.某个与正整数有关的命题,能由![]() 时命题成立推得
时命题成立推得![]() 时命题成立,若已知
时命题成立,若已知![]() 是命题不成立,则以下推理结论正确的是( )
是命题不成立,则以下推理结论正确的是( )
A.![]() 是此命题不成立
B.
是此命题不成立
B.![]() 是此命题不成立
是此命题不成立
C.![]() 是此命题不成立
D.如果
是此命题不成立
D.如果![]() 时命题成立,那么对任意
时命题成立,那么对任意![]() ,此命题成立
,此命题成立
4.上一个n层台阶,若每次可上一层或两层,设所有不同的上法的总数为![]() ,则下列猜想中正确的是( )
,则下列猜想中正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.设![]() 则
则![]() 是( )
是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.已知复数z的模为2,则![]() 的最大值为( )
的最大值为( )
A.1
B.2
C.![]() D.3
D.3
7.![]() 在复平面内表示的点在( )
在复平面内表示的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.若复数![]() 对应的向量为
对应的向量为![]() ,复数
,复数![]() 对应的向量为
对应的向量为![]() ,
,![]() ×
×![]() 则等于( )
则等于( )
A.10
B.8
C.![]() D.4
D.4
9.当![]() 时,
时,![]() 的值等于( )
的值等于( )
A.1
B.-1
C.![]() D.
D.![]()
10.若方程![]() ,则方程的根为( )
,则方程的根为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11.设复数![]() ,则复数
,则复数![]() 的虚部等于 .
的虚部等于 .
12.复数z满足![]() ,那么
,那么![]() .
.
13.类比推理的一般步骤① ;② .
14.如果![]() 且
且![]() ,则
,则![]() .
.
15.在复平面上,正方形ABCD的两个顶点A,B对应的复数分别为 1+2i,3-5i.求另外两个顶点C,D对应的复数.
16.已知复数z1满足(1+i)z1=-1+5i, z2=a-2-i, 其中i为虚数单位,a∈R, 若![]() <z1,求a的取值范围.
<z1,求a的取值范围.
17.若有A、B、C三个不同大小的数字,你能设计一个算法,找出其中的最大值吗?试给出解决问题的一种算法,并画出流程图.
18.旅馆里住着6位旅客,他们分别来自:北京(B)、天津(T)、上海(S)、扬州(Y)、南京(N)和杭州(H).
他们分别姓赵、钱、孙、李、周和吴,还知道:(1)老赵和北京人都是医生,老周和天津人都是教师,老孙和上海人都是工程师;(2)扬州人和老钱、老吴都是退伍军人,而上海人从未参过军;(3)南京人和扬州人都比老赵岁数大,杭州人人比老钱的岁数大,老吴最年轻;(4)老钱和北京人将一起去扬州,老孙和南京人要去广州.
试根据条件确立每位旅客的籍贯.
选修2-1参考答案
第1章 统计案例
§1.1独立性检验
经典例题:根据题意,列出列联表如下:
| 晕机 | 不晕机 | 合计 | |
| 男 | 24 | 31 | 55 |
| 女 | 8 | 26 | 34 |
| 合计 | 32 | 57 | 89 |
提出统计假设,![]() :在恶劣气候飞行中男人与女人一样容易晕机则
:在恶劣气候飞行中男人与女人一样容易晕机则
![]()
![]() ,故我们有90%的把握认为在这次航程中男人比女人更容易晕机.
,故我们有90%的把握认为在这次航程中男人比女人更容易晕机.
当堂练习:
1.C; 2.A; 3.A; 4.B; 5.A; 6.B; 7. 7.86;服用此药的效果与患者的性别有关. ; 8. ③; 9. ③;
10.在酗酒的人中患病的概率为![]() =15%
=15%
在不酗酒的人中患病的概率为![]() =6.7%
=6.7%
因此,酗酒与否,其患肝病的可能性有较大差异,故患肝病与酗酒有关.
患肝病与酗酒有关。
11.提出统计假设,![]() :患慢性病与服用新药无关
:患慢性病与服用新药无关
根据列联表中的数据,可以求得: ![]()
当统计假设![]() 成立时,
成立时,![]() 的概率约为10%,而这里
的概率约为10%,而这里![]()
∴我们不能否定![]() ,即根据目前的调查数据,不能作出患慢性病是否与服用新药有关的结论.
,即根据目前的调查数据,不能作出患慢性病是否与服用新药有关的结论.
| 主食蔬菜 | 主食肉类 | 合计 | |
| 六十岁以下 | 21 | 33 | 54 |
| 六十岁以下 | 43 | 27 | 70 |
| 合计 | 64 | 60 | 124 |
12..(1)2×2的列联表如右:
(2) 提出统计假设,![]() :
:
假设人的饮食习惯与年龄无关,
![]()
当统计假设![]() 成立时,
成立时,![]() 的概率约为2.5%,即有97.5%的把握认为“人的饮食习惯与年龄有关”.
的概率约为2.5%,即有97.5%的把握认为“人的饮食习惯与年龄有关”.
§1.2回归分析
经典例题:
(1)![]() ,
, ![]()
![]()
![]() . 由小概率0.05及
. 由小概率0.05及![]() 查得
查得![]()
∵ ![]() , ∴
, ∴ ![]() 与
与![]() 具有相关关系.
具有相关关系.
(2) ![]() ,
,![]()
∴ 回归直线方程为:![]() ,当
,当![]() 时,
时,![]() .
.
即计高一体重为78kg的学生在高二时的体重约为81kg.
当堂练习:
1.D; 2.B; 3.C; 4.A; 5.C; 6.A; 7. 0; 8. ③; 9. ④⑤;
10.15.
11. (1)6.2人;(2)11人,30人.
12.(1)散点图如下图
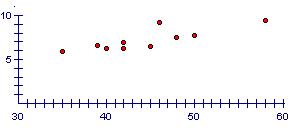
(2)![]()
![]()
![]() ,
,![]()
(3)由散点图知:能用线性回归方程来刻画![]() 与
与![]() 之间的关系,设回归直线为
之间的关系,设回归直线为![]()
![]()
![]()
![]()
![]()
∴ 线性回归方程为:![]()
§1.3统计案例单元测试
1.B; 2.A; 3.D; 4.A; 5.C; 6.C; 7.B; 8.C; 9. 64%;10.女教授人数,男教授人数,女副教授人数,男副教授人数; 11. 5%; 12. 一个地区受过9年或更少教育的百分比每增加1%,收入低于官方规定的贫困线的人数占本州人数的百分比将增加0.8%左右, 大于0;
13. 解:(1)2×2的列联表
| 性别 休闲方式 | 看电视 | 运动 | 总计 |
| 女 | 43 | 27 | 70 |
| 男 | 21 | 33 | 54 |
| 总计 | 64 | 60 | 124 |
(2)假设“休闲方式与性别无关”
计算![]()
因为![]() ,所以有理由认为假设“休闲方式与性别无关”是不合理的,
,所以有理由认为假设“休闲方式与性别无关”是不合理的,
即有97.5%的把握认为“休闲方式与性别有关”
14 解:首先设变量![]() ,题目所给的数据变成如下表所示的数据
,题目所给的数据变成如下表所示的数据
|
| 1 | 0.5 | 0.33 | 0.2 | 0.1 | 0.05 | 0.03 | 0.02 | 0.01 | 0.005 |
|
| 10.15 | 5.52 | 4.08 | 2.85 | 2.11 | 1.62 | 1.41 | 1.30 | 1.21 | 1.15 |
经计算得![]() ,从而认为
,从而认为![]() 与y之间具有线性相关关系,
与y之间具有线性相关关系,
由公式得![]()
所以![]()
最后回代![]() ,可得
,可得![]()
第2章 推理与证明
经典例题:
[解] ![]()
![]()
![]() ┅┅
┅┅
![]()
将以上各式分别相加得:![]()
所以: ![]()
![]()
当堂练习:
1.B; 2.C; 3.C; 4.D; 5.B; 6.B; 7. A; 8.D;
9.D; 10.C; 11.A; 12.B;13.![]() ; 14.
; 14. ![]() ; 15.
f(2.5)>f(1)>f(3.5); 16. 5;
; 15.
f(2.5)>f(1)>f(3.5); 16. 5; ![]() ;
;
17.证明:假设![]() 、
、![]() 、
、![]() 为同一等差数列的三项,则存在整数m,n满足
为同一等差数列的三项,则存在整数m,n满足
![]() =
=![]() +md ①
+md ① ![]() =
=![]() +nd ②
+nd ②
①![]() n-②
n-②![]() m得:
m得:![]() n-
n-![]() m=
m=![]() (n-m) 两边平方得: 3n2+5m2-2
(n-m) 两边平方得: 3n2+5m2-2![]() mn=2(n-m)2
mn=2(n-m)2
左边为无理数,右边为有理数,且有理数![]() 无理数
无理数
所以,假设不正确。即 ![]() 、
、![]() 、
、![]() 不能为同一等差数列的三项
不能为同一等差数列的三项
18. ![]() ABC是直角三角形; 因为sinA=
ABC是直角三角形; 因为sinA=![]()
据正、余弦定理得 :(b+c)(a2-b2-c2)=0;
又因为a,b,c为![]() ABC的三边,所以 b+c
ABC的三边,所以 b+c![]() 0
0
所以 a2=b2+c2 即![]() ABC为直角三角形.
ABC为直角三角形.
19.平行; 提示:连接BD,因为E,F分别为BC,CD的中点, EF∥BD.
20.提示:用求导的方法可求得![]() 的最大值为0
的最大值为0
21.证明:![]()
![]() =
=![]()
![]()
![]() 为△ABC三边,
为△ABC三边,![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
22.(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
23.解(I)从第n年初到第n+1年初,鱼群的繁殖量为axn,被捕捞量为bxn,死亡量为
![]()
![]()
(II)若每年年初鱼群总量保持不变,则xn恒等于x1, n∈N*,从而由(*)式得
![]() 因为x1>0,所以a>b. 猜测:当且仅当a>b,且
因为x1>0,所以a>b. 猜测:当且仅当a>b,且![]() 时,每年年初鱼群的总量保持不变.
时,每年年初鱼群的总量保持不变.
24. 证明:1)![]()
=![]() =
=![]()
2) ![]()
![]()
![]() ① 又
① 又![]() ②
②
由①②知![]() =
=![]() 所以
所以![]()
25.简证:令![]() ,则有
,则有![]() ,再令
,再令![]() 即可
即可
26.证明:设![]()
设![]() 是
是![]() 上的任意两个实数,且
上的任意两个实数,且![]() ,
,
![]()
因为![]() ,所以
,所以![]() 。所以
。所以![]() 在
在![]() 上是增函数。
上是增函数。
由![]() 知
知![]() 即
即![]() .
.
§2.3 推理与证明单元测试
1.B; 2.C; 3.D; 4.A; 5.D; 6.A; 7. B; 8. 大前提和推理过程; 9. 增函数的定义;
10. 侧面都是全等的三角形; 11. 等差; 12. a≤b;
13. 解:在数列{an}中,∵![]()
∴![]()
∴可以猜想,这个数列的通项公式是![]()
14. 证明:(用综合法) ∵![]() ,
,
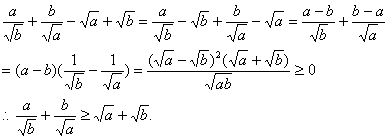 ;
;
第3章 数系的扩充与复数的引入
§3.1复数的概念
经典例题:
解析:由![]() ,可知
,可知![]() ,代入
,代入![]() 得:
得:
![]()
![]() ,即
,即![]()
![]()
![]()
则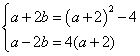 ,解得
,解得![]() 或
或![]() 。
。
当堂练习:
1.B; 2.D; 3.B; 4.B; 5.D; 6.A; 7. B; 8.D;
9.C; 10.B; 11. ![]() ,
,![]() ; 12. 1,
; 12. 1,![]() ;13.
;13. ![]() ; 14. 1;
; 14. 1;
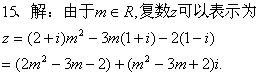
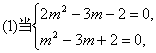

16.解:![]()
![]()
![]()

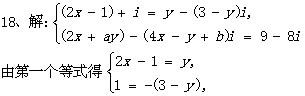
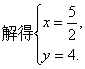 将上述结果代入第二个等式中得
将上述结果代入第二个等式中得

§3.2-3复数的四则运算及几何意义
经典例题:分析:本题考查两个复数相等的充要条件.方程的根必适合方程,设x=m为方程的实根,代入、整理后得a+bi的形式,再由复数相等的充要条件得关于k、m的方程组,求解便可.
解:设x=m是方程的实根,代入方程得
m2+(k+2i)m+2+ki=0,即(m2+km+2)+(2m+k)i=0.
由复数相等的充要条件得![]()
解得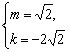 或
或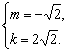
∴方程的实根为x=![]() 或x=-
或x=-![]() ,相应k的值为-2
,相应k的值为-2![]() 或2
或2![]() .
.
当堂练习:
1.C; 2.A; 3.B; 4.B; 5.B; 6.C; 7. B; 8.C;
9.A; 10.B; 11. z = i –1; 12. 1;13. 2i; 14. x2=y-1,x∈(0,1![]() ;
;
15.解;
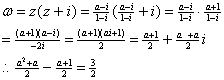 即
即![]()
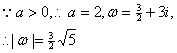
16.提示: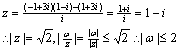 因
因![]()
![]()
![]() 故a的取值范围是
故a的取值范围是![]()
17.原方程化简为![]() , 设z=x+yi(x、y∈R),代入上述方程得 x2+y2+2xi=1-i,
, 设z=x+yi(x、y∈R),代入上述方程得 x2+y2+2xi=1-i,
∴x2+y2=1且2x=-1,解得x=-![]() 且y=±
且y=±![]() , ∴原方程的解是z=-
, ∴原方程的解是z=-![]() ±
±![]() i.
i.
18. 解:如下图.因为点A对应的复数为1,直线l过点A且平行于虚轴,所以可设直线l上的点对应的复数为z=1+bi(b∈R).
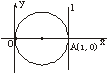
因此![]()
![]() .设
.设![]() =x+yi(x、y∈R),于是x+yi=
=x+yi(x、y∈R),于是x+yi=![]() i.根据复数相等的条件,有
i.根据复数相等的条件,有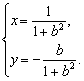 消去b,
消去b,
有x2+y2=![]() =
=![]() =
=![]() =x.所以x2+y2=x(x≠0),即(x-
=x.所以x2+y2=x(x≠0),即(x-![]() )2+y2=
)2+y2=![]() (x≠0).所以
(x≠0).所以![]() 所对应的点的集合是以(
所对应的点的集合是以(![]() ,0)为圆心,
,0)为圆心,![]() 为半径的圆,但不包括原点O(0,0).
为半径的圆,但不包括原点O(0,0).
§3.4 数系的扩充与复数的引入单元测试
1.D; 2.B; 3.C; 4.B; 5.B; 6.C; 7. A; 8.A;
9.B; 10.C; 11. ![]() ; 12.
; 12. ![]() ;13.
;13. ![]() ; 14.
; 14. ![]() ,
,![]() ;
;
15、解:
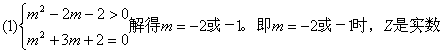
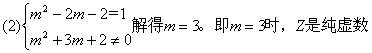
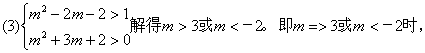
Z对应的点位于复平面的第一象限
16、
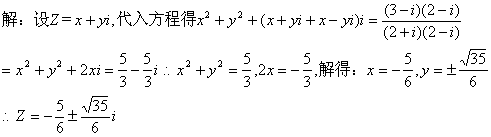
17、

18、
19、解: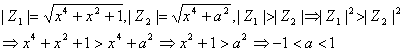
20、解:![]()
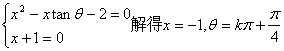
§4.1-2流程图、结构图
经典例题:
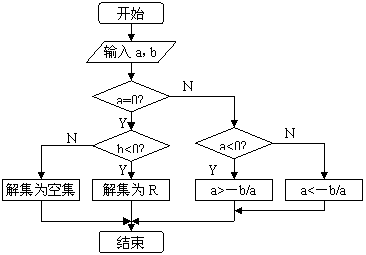 |
当堂练习:
1.D; 2.A; 3.A; 4.C; 5.B; 6.B; 7. 顺序 条件(选择) 循环; 8. 具体,抽象 (其他类似答案也可); 9. 2;
 10.
10.
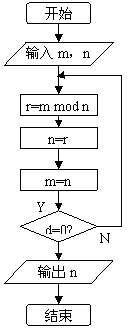 11. 解:(1)计算的是2006和1600的最大共约数
11. 解:(1)计算的是2006和1600的最大共约数
(2)设置两个数较大数为M,较小数为N,
第一步,计算m除n的余数r;
第二步,除数变成被除数,余数变成除数
第三步,回到第一步,直到余数为0
选修1-2综合测试
1.C;
2.B; 3.B; 4.B; 5.D; 6.D; 7.B; 8.A; 9.B; 10.D; 11.1; 12.![]() ; 13.①通过观察个别情况发现某些相同性质;②从已知的相同性质中推出一个明确表达的一般性结论;14.2006;
; 13.①通过观察个别情况发现某些相同性质;②从已知的相同性质中推出一个明确表达的一般性结论;14.2006;
15.解:设D(x,y)
![]()
![]()
![]()
![]()
![]()
由![]()
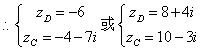
16.解:由题意得 z1=![]() =2+3i,
=2+3i,
于是![]() =
=![]() =
=![]() ,
,![]() =
=![]() .
.
![]() <
<![]() ,得a2-8a+7<0,1<a<7.
,得a2-8a+7<0,1<a<7.
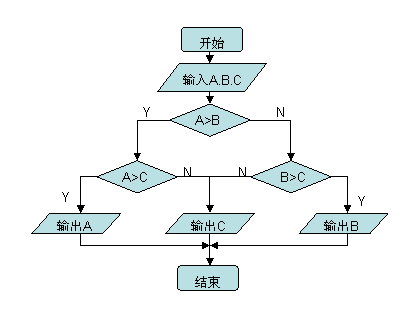
17. 解:应该先两两比较,算法和流程图如下:
S1 输入A、B、C;
S2 如果A>B,那么转S3,否则转S4;
S3 如果A>C,那么输出A,转S5,否则输出C,转S5;
S4 如果B>C,那么输出B,转S5,否则输出C;
S5 结束。
| B | T | S | Y | N | H | |
| 赵 | \ | \ | \ | \ | \ | |
| 钱 | \ | \ | \ | \ | \ | |
| 孙 | \ | \ | \ | \ | \ | |
| 李 | \ | \ | \ | \ | \ | |
| 周 | \ | \ | \ | \ | \ | |
| 吴 | \ | \ | \ | \ | \ |
18.
根据条件(1):老赵不是北京人,老周不是天津人,老孙不是上海人.再根据职业不同可断定:老周和老孙都不是北京人,老赵和老周都不是上海人,老赵和老周都不是上海人,老赵和老孙都不是天津人,在表中相应划上斜线表示不可能.根据条件(2):可划去钱(Y),吴(Y),钱(S),吴(S).根据条件(3):可划去赵(N),赵(Y),钱(H),吴(S),吴(S).根据条件(4):可划去钱(B),孙(N),钱(N).
最后再观察表上空格,可以断定老赵是杭州人,老钱是天津人,就可划去孙(H),可知老孙是扬州人,或划去周(Y),周(H),可知老周是南京人,从而可知,老吴是北京人,老李是上海人.
所以,老赵是杭州人,老钱是天津人,老孙是扬州人,老李是上海人,老周是南京人,老吴是北京人.