2.2 直线、平面平行的判定及其性质
一、选择题
1、a∥
，则a平行于内的(D )
A、一条确定的直线
B、任意一条直线
C、所有直线
D、无数多条平行线
2、如果直线a∥平面，那么直线a与平面内的(D )
A、一条直线不相交
B、两条直线不相交
C、无数条直线不相交
D、任意一条直线都不相交
3、m、n是平面
外的两条直线，在m∥的前提下，m∥n是n∥的( )
A、充分而不必要条件 B、必要而不充分条件
C、充分必要条件 D、既不充分也不必要条件
4、直线a∥面，面内有n条互相平行的直线，那么这n条直线和直线a( )
A、全平行 B、全异面
C、全平行或全异面 D、不全平行也不全异面
5、直线a∥平面，平面内有n条直线相交于一点，那么这n条直线中与直线a平行的( )
A、至少有一条 B、至多有一条
C、有且只有一条 D、不可能有
6、a和b是两条异面直线，下列结论正确的是( )
A、过不在a、b上的任意一点，可作一个平面与a、b都平行
B、过不在a、b上的任意一点，可作一条直线与a、b都相交
C、过不在a、b上的任意一点，可作一条直线与a、b都平行
D、过a可以并且只可以作一个平面与b平行
二、填空题
7、若直线a∥平面 
，直线b∥平面，且 a
，b，且 ∩=c，则 a、b的位置关系是
8、若直线 a ∥平面 ，直线b∥ 平面，a，b,则a、b的位置关系是＿
三、判断题
9、
a∥ ( )
10、若直线a与平面内的无数条直线平行，则a∥ （ ）；
三、解答题
11、如图，异面直线
、
，
，
，
为
中点，
，
，
，
，
，
，求：
为
中点。
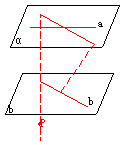
12、三个平面两两相交不共线，求证三条直线交于一点或两两平行。
13、、异面直线，
为空间任一点，过作直线
与、均相交，这样的直线可以作多少条。
14、如图，已知异面直线AB、CD都平行于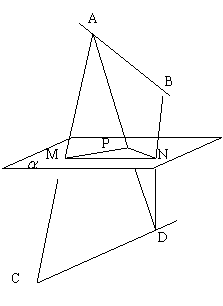
平面，且AB、CD在两侧，若AC、BD与分别交于M、N两点、求证：
。
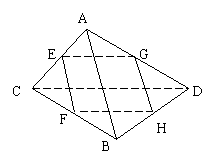
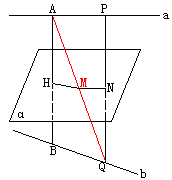
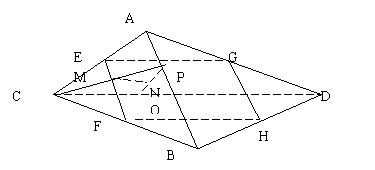
15、如图：线段AB、CD所在的直线是异面直线，E、F、G、H分别是线段AC、CB、BD、DA的中点，P、Q两点分别是AB和CD上的任意点，求证：PQ被平面EFGH平分、
 |
参考答案
一、选择题
1、D；2、D；3、A；4、C；5、B；6、D
二、填空题
7、a∥b
8、平行或异面
三、判断题
9、错
10、错
四、解答题
11、证：连
交于
，连
、
∴ 
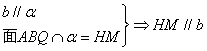
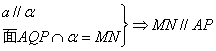
12、证：设
，
，
∴ 、
（1）若
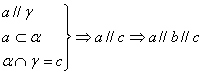
（2）若
∴ 、、
交于一点
13、解：
，
或无数。
过存在唯一个平面
过存在唯一个平面
① 若或
，有无数条
② 若
或，且
且
直线不存在
③ 
且
，有且只有一条。
，过、作平面
∴ 
∴ 
连与相交
∴ 存在与、均相交
假设有两条过的直线
、
与、均相交
，确立平面
与、各有一个交点
∴ 
同理
，与、异面矛盾
∴ 假设不成立
∴ 只有一条
 |
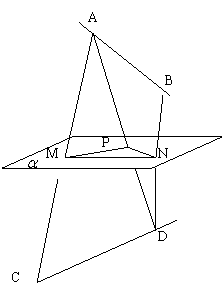14、证明：连AD交于P，连MP、PN
CD∥
平面ACD∩=MP CD∥MP
CD
同理AB∥PN
15、证明：PQ∩平面EEFGH=N，
连PC，设PC∩EF=M
平面PCQ∩平面EFGH=MN，
CQ∥平面EFGH
∴MN∥CQ
因为EF是△ABC的中位线，所以M是CP的中点，则N是PQ的中点，
即 PQ被平面EFGH平分
 |