2.2 直线、平面平行的判定及其性质
一、选择题
1、直线a，b异面直线，直线a和平面a平行，则直线b和平面a的位置关系是（ ）
A、bÌa B、b∥a C、b与a相交 D、以上都有可能
2、如果点M是两条异面直线外的一点，则过点M且与a，b都平行的平面 （ ）
A、只有一个 B、恰有两个
C、或没有，或只有一个 D、有无数个
3、不同直线
和不同平面
，给出下列命题
① 
② 
③ 
④ 
其中假命题有： （ ）
A、0个 B、1个 C、2个 D、3个
4、如果△ABC的三个顶点到平面
的距离相等且不为零，那么△ABC的( )
A、三边均与平行
B、三边中至少有一边与平行
C、三边中至多有一边与平行
D、三边中至多有两边与平行
5、下列命题正确的是( )
A、一条直线与一个平面平行，它就和这个平面内的任意一条直线平行
B、平行于同一个平面的两条直线平行
C、与两个相交平面的交线平行的直线，必平行于这两个平面
D、平面外的两条平行直线中的一条与一个平面平行，则另一条直线也与此平面平行
二、填空题
6、直线a∥b，a∥平面
，则b与平面的位置关系是________
7、A是两异面直线a、b外的一点，过A最多可作________个平面同时与a、b平行
8、过两条平行直线中的一条，可以作________个平面平行于另一条直线
9、若平面及这个平面外的一条直线l同时垂直于直线m，则直线l和平面的位置关系是________
10、与空间四边形ABCD四个顶点距离相等的平面共有________个
11、若直线________，则l不可能与平面a内无数条直线都相交
三、解答题
12、
、
、
两两异面，空间与、、，均相交的直线有多少条？
13、
，
，
，求证：
。
14、已知直线a∥平面
，点A∈直线b。
A∈，a∥b，求证：b
、
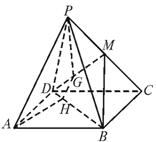
15、已知ABCD是平行四边形，点P是平面ABCD外一点，M是PC的中点，在DM上取一点G，过G和AP作平面交平面BDM于GH，求证：AP∥GH、
参考答案
一、选择题
D；2、C；3、D；4、C；5、D
二、填空题
6、
7、1个
8、无数个
9、
10、7
11、
三、解答题
12、证：存在，
，
，
存在，
，
与、异面，中有无数个点在、外
每一个点可作一条线与、均相交
∴ 无数条
13、证：过作
∴ 
过作
∴ 
∴ 
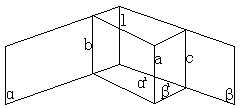
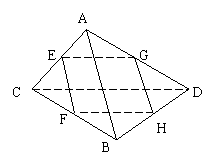14、证明：假设b 
，平面过a与A，∩=
，
∵a∥ ∴a∥
又∵b∩=A，且a∥b
∴过点A与a平行的直线有两条b、
这与“过直线外一点有且只有一条直线与已知直线平行”相矛盾。
∴ b
15、证明：连结AC，设AC交BD于O，连结MO、
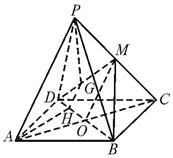
∵ 四边形ABCD是平行四边形，
∴ O是AC的中点、
又M是PC的中点，
∴ MO∥PA、
又MO面BDM、PA面BDM、
∴ PA∥面BDM、
又经过PA与点G的平面交面BDM于GH、
∴ AP∥GH、