高三数学第一轮复习训练题
数学（二十）（理科 导数与复数）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1.函数y = (1－sinx)
的导数是
(A) y=2sin2x-cosx (B) y=sin2x+2cosx (C) y=2sin2x-2cosx (D) y=sin2x-2cosx
2.设
，则
等于
A -1 B 1 C 0 D 任意实数
3.复数
等于
A．
B．
C．
D．
4..函数
=
，则
=
A 0 B 1 C2006 D 2007
5.在复平面内，复数
对应的点位于
A 第一象限 B 第二象限 C 第三象限 D 第四象限
6．曲线
在点(1 ，
)处切线的倾斜角为
A.
B.
C. 
D.
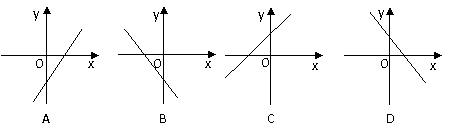
7．
的图象开口向上，且顶点在第二象限，则
的图象大概是：
 |
8.设
是定义在R上的偶函数，当
时，
，且
，则不等式
的解集为
A．（－1，0）∪（1，+
） B．（－1，0）∪（0，1）
C．（－，－1）∪（1，+） D．（－，－1）∪（0，1）
9.对于R上可导的任意函数f（x），若满足（x－1）
³0，则必有
A.f（0）＋f（2）<2f（1） B. f（0）＋f（2）£2f（1）
C. f（0）＋f（2）³2f（1） D. f（0）＋f（2）>2f（1）
10.函数
的单调减区间是
A．
B．
C．
及 D．
11.已知
A．1+2i B。1-2i C。2+i D。2
12.已知f＇（0）=2，则
=
A．4 B．－8 C．0 D．8
二、填空题：本大题共4小题；每小题4分，共16分，把答案填在题中的横线上。
13.已知函数
在R上可导，函数
，则
--
14.f（x）= 1+3sin x + 4cos x取得最大值时tan x =
15.设
、
为实数，且
，则+=_________
16.设
分别是定义在R上的奇函数和偶函数，当
时，
且
则不等式
的解集是
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或推演步骤。
17.已知
，求
的值
18.设t≠0，点P（t,0）是函数f（x）=x3+ax与g（x）=bx2+c的图象的一个公共点，两函数的图象在点P处有相同的切线..
（1）用t表示a，b，c；
（2）若函数y=f（x）－g（x）在（－1，3）上单调递减，求t的取值范围.
19.已知函数
,(a
R),设曲线
在点(1 
)处的切线为
,若与圆C: 
相切，求a的值
20.已知函数
（1）求函数f (x)的单调区间；
（2）求证：x
> 1时，
21.已知函数
，求函数在[1，2]上的最大值.
22.设函数与数列
满足关系：(1) a1.>a, 其中a是方程
的实根，(2) an+1=
( nN+ ) ,如果的导数满足0<
<1
（1）证明： an>a （2）试判断an与an+1的大小，并证明结论。
2008－2009学年度祁东二中高三第一轮复习训练题
数学（二十）（理科 导数与复数）参考答案
一 DBABD DCACA CD
二 13. 0 14. 
15. 4 16. 
三．17．解：
=
18．解：（1）
由
①
由已知得：
② 
③
联立①②③得：
（2）由题意
恒成立.
由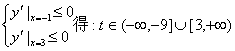
19．解：依题意有：= a, =2ax+
(x<2)
方程为
=0
与圆相切 
=
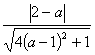a=
20．解 1）依题意知函数的定义域为x > 0. 
，
所以，当a≤0时，f (x)的单调递增区间为（0，+∞）
当
时，
，令
，有
；
所以函数f (x)的单调递增区间为
；令
，有
所以函数f (x)的单调递减区间为
.
（2）设
时，
，
所以g (x)在（1，+∞）上是增函数，
∴当x>1时，
21．解：∵，
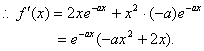
令
是减函数，在（0，
）上是增函数.
（i）当0<<1，即a>2时，f(x)在（1，2）上是减函数， ∴
.
（ii）当
时， ∴ f(x)在（1，）是增函数，在（，2）上是减函数，
（ii）当>2时，即0<a<1时，f
(x)在（1，2）上是增函数，
∴f(x)max= f (2)=4e－2a.…
综上所述，当0< a <1时，f (x)的最大值为4e－2a，
当1≤a≤2时，f (x)的最大值为
，
当a >2时，f (x)的最大值为e－a
22．证明：(1)当n=1时，由题设知a 1> a成立。
假设n=k时,
a k> a成立
(k
)，
由>0知增函数，则
，
又由已知:
=a，
于是a k+1> a ，即对n=k+1时也成立，
故 对任意正整数n, a n> a都成立。
解：(2)令
则
故
为增函数
则 当x> a时,有
而
即
由(1)知a n> a 
(
)
故 对任意正整数n都有a n> a n+1。