高三理科数学数学摸底试题
理科
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟。
参考公式
如果事件A、B互斥,那么 P(A+B)=P(A)+P(B)
如果事件A、B相互独立,那么 P(A·B)=P(A)·P(B)
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发
生k次的概率![]()
球的表面积公式 ![]() (其中R表示球的半径)
(其中R表示球的半径)
球的体积公式 ![]() (其中R表示球的半径)
(其中R表示球的半径)
第Ⅰ卷(选择题,共60分)
一、选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的,请把正确的答案填在题后的括号内.)
1、复数![]() 满足
满足![]() ,则
,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2、函数![]() 是( )
是( )
A.周期为![]() 的奇函数 B.周期为
的奇函数 B.周期为![]() 的偶函数
的偶函数
C.周期为![]() 的奇函数
D.周期为
的奇函数
D.周期为![]() 的偶函数
的偶函数
3、![]() ( )
( )
A.充分但不必要条件 B.必要但不充分条件
C.充分且必要条件 D.既不充分也不必要条件
4、等差数列![]() 的公差为2,若
的公差为2,若![]() 、
、![]() 、
、![]() 成等比数列,则
成等比数列,则![]() =( )
=( )
 A.-6 B.-8 C.8 D.6
A.-6 B.-8 C.8 D.6
5、设函数f(x)= ,则![]() 的值为
的值为
A、a B、b C、min{a,b}.D、max{a,b}
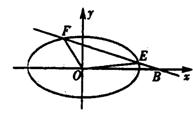
6、已知双曲线![]() 两条准线间的距离为
两条准线间的距离为![]() ,则双曲线的离心率是( )
,则双曲线的离心率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、已知![]() 是两条不重合的直线,
是两条不重合的直线,![]() 是两个不同的平面,则下列命题正确的是( )
是两个不同的平面,则下列命题正确的是( )
A. 若![]() 则
则![]() B. 若
B. 若![]() ,
,![]() ,则
,则![]()
C. 若![]() ,
,![]() 则
则![]() D. 若
D. 若![]() ,
,![]() 则
则![]()
8、口袋中放有大小相等的两个红球和一个白球,有放回地每次摸取一个球,定义数列![]() ,
,![]() ,如果
,如果![]() 为数列
为数列![]() 的前
的前![]() 项和,那么
项和,那么![]() 的概率为( )
的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9.已知![]() 是定义在实数集R上的函数,它的反函数为
是定义在实数集R上的函数,它的反函数为![]() ,若
,若![]()
|
A.2 B.1 C.0 D.-1
10、定义行列式运算: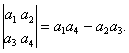 将函数
将函数 的图象向左平移
的图象向左平移![]() 个单位
个单位![]() ,所得图象对应的函数为偶函数,则
,所得图象对应的函数为偶函数,则![]() 的最小值是( )
的最小值是( )
A. ![]() B.
B.![]() C.
C. ![]() D.
D.
![]()
11、等差数列![]() 的公差d不为零,Sn是其前n项和,则下列四个命题中的假命题是( )
的公差d不为零,Sn是其前n项和,则下列四个命题中的假命题是( )
A.若d<0,且S3=S8,则{Sn}中,S5和S6都是{Sn}中的最大项
B.给定n,对于一定![]() ,都有
,都有![]()
C.若d>0,则{Sn}中一定有最小的项
D.存在![]() ,使
,使![]() 同号
同号
12、抛物线![]() 的准线l与y轴交于点P,若l绕点P以每秒
的准线l与y轴交于点P,若l绕点P以每秒![]() 弧度的角速度按逆时针方向旋转t秒钟后,恰与抛物线第一次相切,则t等于
弧度的角速度按逆时针方向旋转t秒钟后,恰与抛物线第一次相切,则t等于
A.1 B.2 C.3 D.4
第Ⅱ卷(非选择题共90分)
二、填空题:(本大题共4小题,每小题4分,共16分。把答案填在题中横线上。)
13.在约束条件 下,目标函数
下,目标函数![]() =
=![]() 的最大值为
.
的最大值为
.
14. 若体积为![]() 的球面上三点
的球面上三点![]() 满足
满足![]() ,
,![]() ,则球心到平面
,则球心到平面![]() 的距离为
.
的距离为
.
15.已知![]() 展开式中第4项为常数项,则展开式的各项的系数和为 .
展开式中第4项为常数项,则展开式的各项的系数和为 .
|
三、解答题:(本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。)
17、(本小题满分12分)
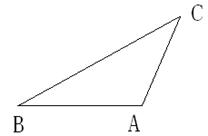 如图,在
如图,在![]() 中,
中,![]() .
.
(Ⅰ)求![]() ;
;
(Ⅱ) 记![]() 的中点为
的中点为![]() ,求中线
,求中线![]() 的长。
的长。
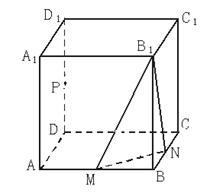
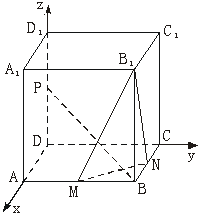
18、(本小题满分12分)
正方体![]() 中,
中,![]() 分别为棱
分别为棱![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)设二面角![]() 为
为![]() ,求
,求![]() 的值。
的值。
19、(本小题满分12分)
某公司欲建连成片的网球场数座,用128万元购买土地10000平方米,该球场每座的建筑面积为1000平方米,球场的总建筑面积的每平方米的平均建筑费用与球场数有关,当该球场建n个时,每平方米的平均建筑费用用![]() 表示,且
表示,且![]()
![]() (其中
(其中![]() ),又知建五座球场时,每平方米的平均建筑费用为400元,为了使该球场每平方米的综合费用最省(综合费用是建筑费用与购地费用之和),公司应建几个球场?
),又知建五座球场时,每平方米的平均建筑费用为400元,为了使该球场每平方米的综合费用最省(综合费用是建筑费用与购地费用之和),公司应建几个球场?
20、(本小题满分12分)
设![]() ,函数
,函数![]() (1)讨论
(1)讨论![]() 的单调性;
的单调性;
(2)求![]() 在区间
在区间![]() 上的最小值。
上的最小值。
21、(本小题满分12分)
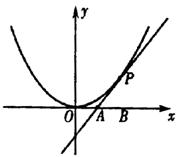 如图,已知直线
如图,已知直线![]() 与抛物线
与抛物线![]() 相切于点P(2,1),且与
相切于点P(2,1),且与![]() 轴交于点
轴交于点![]() ,O为坐标原点,定点B的坐标为(2,0).
,O为坐标原点,定点B的坐标为(2,0).
(I)若动点![]() 满足
满足![]() ,
,
求动点![]() 轨迹
轨迹![]() 的方程;
的方程;
(II)若过点B的直线![]() (斜率不等于零)与(I)
(斜率不等于零)与(I)
中的轨迹![]() 交于不同的两点E、F(E在B、F之间),
交于不同的两点E、F(E在B、F之间),
试求△OBE与△OBF面积之比的取值范围。
22.(本小题满分14分)
已知数列![]()
![]()
(I)若a1=2,证明![]() 是等比数列;
是等比数列;
(II)在(I)的条件下,求![]() 的通项公式;
的通项公式;
(III)若![]() ,证明数列{
,证明数列{![]() }的前n项和Sn满足Sn<1.
}的前n项和Sn满足Sn<1.
参考答案
理科
一选择题、1-5:BBAAD 6-10:DCBCC 11-12:DC
二填空题、13、2 14、![]() 15、
15、![]() 16、
16、![]()
三解答题、
17.解: (Ⅰ)由![]() ,
, ![]() 是三角形内角,得
是三角形内角,得![]() ………2分
………2分
∴ ![]() ……………5分
……………5分
![]() ………………………………6分
………………………………6分
(Ⅱ) 在![]() 中,由正弦定理,
中,由正弦定理,![]() ,
,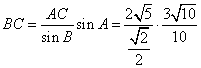
![]() …9分
…9分
![]() ,
, ![]() ,
,
由余弦定理得:![]()
=![]() ………12分
………12分
18、解法一:(1)如图,以D为原点,DA、DC、DD1分别为x轴、y轴、z轴建立空间直角坐标系,取正方体棱长为2,则P(0,0,1)、M(2,1,0)、B(2,2,0)、B1(2,2,2).
∵![]() ·
·![]() =(2,2,-1)·(0,1,2)=0,
=(2,2,-1)·(0,1,2)=0,
∴MB1⊥PB,同理,知NB1⊥PB.
∵MB1∩NB1=B1,∴PB⊥平面MNB1.
(2)∵PB⊥平面MNB1,BA⊥平面B1BN,
∴![]() =(2,2,-1)与
=(2,2,-1)与![]() =(0,2,0)所夹的角即为α,cosα=
=(0,2,0)所夹的角即为α,cosα=![]() =
=![]() .
.
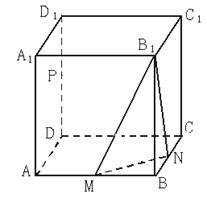
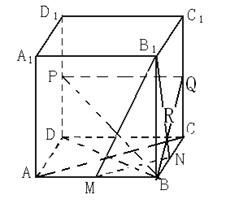
解法二:(1)、如图:连结PB, DB, AC, MN

过点P作垂直CC垂足于Q,可知PD垂直平面![]() ,连结BQ,
,连结BQ,![]()
则![]()
![]()
![]() (由三垂线定理) 4分
(由三垂线定理) 4分
![]() 6分
6分
(2)、连结MR,可知![]() 8分
8分
设正方体的棱长为2,依题可知![]() 10分
10分
![]() 12分
12分
19.
|
由题意知f(5)=400, f(x)=f(5)(1+![]() )=400(1+
)=400(1+![]() )
)
从而每平方米的综合费用为y=f(x)+![]() =20(x+
=20(x+![]() )+300≥20.2
)+300≥20.2![]() +300=620(元),
+300=620(元),
当且仅当x=8时等号成立
故当建成8座球场时,每平方米的综合费用最省.
20.解:函数![]() 的定义域为
的定义域为![]() ,
,![]() 。(
。(![]() ) (2分)
) (2分)
由![]() ; (3分)
; (3分)
由![]() ; (4分)
; (4分)
故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减。(5分)
上单调递减。(5分)
(2)①当![]() ,即
,即![]() 时,由(Ⅰ)知
时,由(Ⅰ)知![]() 在
在![]() 上单调递增,
上单调递增,
所以![]()
![]()
![]() ;(6分)
;(6分)
②当![]() 时,由(Ⅰ)知
时,由(Ⅰ)知![]() 在
在![]() 上单调递减,所以
上单调递减,所以![]()
![]()
![]() (7分)
(7分)
③当![]() 时,需比较
时,需比较![]() 与
与![]() 的大小。
的大小。
因为![]() -
-![]()
![]() -
-![]()
![]()
所以,若![]() ,则
,则![]()
![]() ,此时
,此时![]()
![]()
![]() ;(10分)
;(10分)
若![]() ,则
,则![]()
![]() ,此时
,此时![]()
![]()
![]() 。(11分)
。(11分)
综上,当![]() 时
时![]()
![]() ;,当
;,当![]() 时
时![]()
![]() (12分)
(12分)
21.(本小题满分12分)
解:(I)由![]() ,
, ![]()
∴直线l的斜率为![]() , ………………………………………1分
, ………………………………………1分
故l的方程为![]() ,
,
∴点A坐标为(1,0) ………………………………… 2分
设![]() 则
则![]() ,
,
由![]() 得
得
![]()
整理,得![]() ……………5分
……………5分
(II)如图,由题意知直线l的斜率存在且不为零,设l方程为y=k(x-2)(k≠0)①
|
![]() ,
,
由△>0得0<k2<![]() . 设E(x1,y1),F(x2,y2)
. 设E(x1,y1),F(x2,y2)
则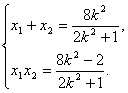 ②………………………………7分
②………………………………7分
令![]() ,
,
由此可得![]()
由②知![]()

![]() .∴△OBE与△OBF面积之比的取值范围是(3-2
.∴△OBE与△OBF面积之比的取值范围是(3-2![]() ,1).…12分
,1).…12分

解法2:![]()
![]()
![]()
![]() ,
,![]()
![]()
![]() 切线PA的方程为
切线PA的方程为![]() ,令y=0得x=1
,令y=0得x=1 ![]()
![]()
|
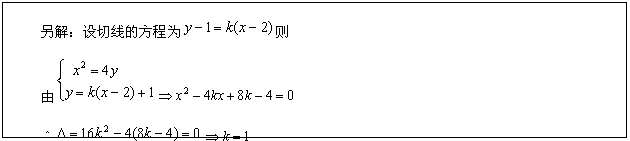 设M(x,y),则
设M(x,y),则由![]()
![]()
![]()
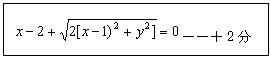 化简得,
化简得,![]() ,
,
故动点M轨迹方程为![]() 。
。
评注:上述两种方法是处理切线问题的基本方法应对此加以理解。
解法3:设![]()
![]() 则
则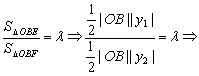
![]() ①
①
因为![]() 所以可设直线的方程为
所以可设直线的方程为![]() 。
。
由![]()
![]()
![]() ②
②
![]() ③
③
![]()
由![]() 得
得![]() 又
又![]() 解得
解得![]()
![]() 的取值范围
的取值范围![]()
![]() 。
。
解法4:设![]()
![]() 则
则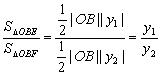
因为![]() 所以可设直线的方程为
所以可设直线的方程为![]()
由![]()
![]()
![]()
![]()
![]()
由![]() 得
得![]() 又
又![]() ,解得
,解得![]()
![]() 的取值范围
的取值范围![]()
![]() 。
。
解法5:设![]()
![]() ,
,![]()
![]() 则
则
![]()
![]() 且
且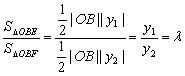 , 又
, 又![]()
![]()
由③![]() ②
②![]()
![]()
结合①②化简得![]() ⑤ 由②⑤得
⑤ 由②⑤得![]()
![]()
![]()
![]()
![]() 的取值范围
的取值范围![]()
![]() 。
。
解法6:
当![]() 趋向于
趋向于![]() 时,
时,![]() :
:![]() 比趋向于1
比趋向于1
当![]() 趋向于0时,
趋向于0时,![]() :
:![]() 比趋向于
比趋向于![]()
![]() 的取值范围
的取值范围![]()
![]() 。
。
评点:请同学们细细品味各种处理问题的方式,学会理性思维合理运算。
22.(本小题满分14分)
解(I)![]() ,
,
由已知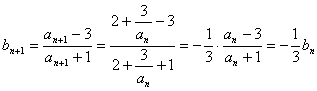 ,
,
![]() 是首项为
是首项为![]() ,公比为
,公比为![]() 的等比数列.…………………………4分
的等比数列.…………………………4分
(II)由(I)知![]() ,
,
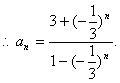 ……………………………………………………6分
……………………………………………………6分
(III)首先证明![]()
①当n=1时,![]() ;………………………………7分
;………………………………7分
②假设![]() …………………………………………………8分
…………………………………………………8分
当![]()
![]() ,
,
![]() ,
,
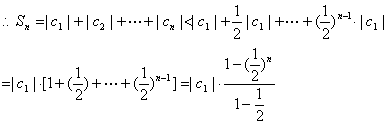
=![]() ,…………………………………………………………12分
,…………………………………………………………12分
![]() ,
,
即![]() ,
,
![]() …………………………………………14分
…………………………………………14分