高三理科数学模拟试卷
理 科
总分:150分 时量:120分钟 供题人:武汉中学高三数学组
一、选择题:本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中有且只有一项是符合题目要求的.
1.复数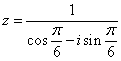 的共轭复数
的共轭复数![]() 是
( )
是
( )
A.![]()
![]() B.
B.![]()
C.![]() D.
D.![]()
2.在各项都为正数的等比数列![]() 中,
中,![]() ,前三项的和为21,则
,前三项的和为21,则![]() ( )
( )
A.33 B.
3.某一计算机网络有![]() 个终端,每个终端在一天中没有使用的概率为
个终端,每个终端在一天中没有使用的概率为![]() ,则这个网络中一天平均使用的终端个数是
( )
,则这个网络中一天平均使用的终端个数是
( )
A .![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.已知m、n是不重合的直线,α、β是不重合的平面,有下列命题,
①若m![]() α, , n∥α,则m∥n, ②若α∩β= n ,m∥n, 则m∥α,且 m∥β
α, , n∥α,则m∥n, ②若α∩β= n ,m∥n, 则m∥α,且 m∥β
③若m∥α,m∥β,则α∥β, ④若m⊥α, m⊥β, 则α∥β
其中正确的命题个数是 ( )
A .1
B
5.湖南经视台某采访小组共有8名记者,现从8名记者中按性别比例选取4名记者分别派往湘潭、株洲、长沙、常德四个地方执行采访任务,已知共有960种不同的安排方式。则其中有男记者 ( )
A.2名 B.4名 C.6名 D.2名或6名
6.定义行列式运算: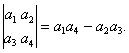 将函数
将函数 的图象向左平移
的图象向左平移![]() 个单位
个单位![]() ,所得图象对应的函数为偶函数,则
,所得图象对应的函数为偶函数,则![]() 的最小值是 ( )
的最小值是 ( )
A. ![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
7.设函数![]() ,若
,若![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B. ![]()
C. ![]() D.
D. ![]()
8.设![]() 是
是![]() 内任一点,且
内任一点,且![]() 设
设![]() 的面积分别为
的面积分别为![]() ,且
,且![]() ,则在平面直角中坐标系中,以
,则在平面直角中坐标系中,以![]() 为坐标的点
为坐标的点![]() 的轨迹图形是 ( )
的轨迹图形是 ( )
 | |||||||
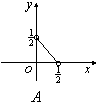 | 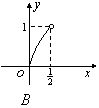 | ||||||
 | |||||||
9.对于集合P、Q, 定义P-Q=![]() ,
,![]() ,设
,设
A=![]() ,B=
,B=![]() ,则
,则![]() 等于
( )
等于
( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
10.椭圆![]() 的左准线为
的左准线为![]() ,左、右焦点分别为
,左、右焦点分别为![]() ,抛物线
,抛物线![]() 的准线也为
的准线也为![]() ,焦点为
,焦点为![]() ,记
,记![]() 与
与![]() 的一个交点为
的一个交点为![]() ,则
,则![]() ( )
( )
A.![]() B
B![]()
二、填空题:本大题共5个小题,共25分,将答案填写在题中的横线上.
11.如果(x-![]() )8的展开式的常数项等于1120,那么实数a的值为____________。
)8的展开式的常数项等于1120,那么实数a的值为____________。
12.为了了解“预防禽流感疫苗”的使用情况,某市卫生部门对本地区9月份至11月份注射疫苗的所有养鸡场进行了调查,根据下列图表提供的信息,可以得出这三个月本地区每月注射了疫苗的鸡的数量平均为 万只.

| 月份 | 养鸡场(个数) |
| 9 | 20 |
| 10 | 50 |
| 11 | 100 |
13.函数![]() 在
在![]() 上的最大值为
上的最大值为
14. 设![]() ,
,
求![]()
 .
.
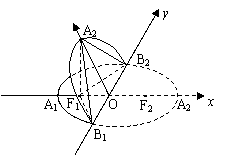
15.如图,椭圆![]() 的长轴为A
的长轴为A![]() 的体积
的体积![]() = 。
= 。
三、解答题:本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
![]() 已知
已知![]() 是
是![]() 的两个内角,
的两个内角,![]() ,(其中
,(其中![]() 是互相垂直的单位向量),若
是互相垂直的单位向量),若
(1)试问![]() 是否为定值,若是定值,请求出,否则请说明理由;
是否为定值,若是定值,请求出,否则请说明理由;
(2)求![]() 的最大值,并判断此时三角形的形状.
的最大值,并判断此时三角形的形状.
17.(本小题满分12分)
 移动公司进行促销活动,促销方案为顾客消费1000元,便可获得奖券一张,每张奖券中奖的概率为
移动公司进行促销活动,促销方案为顾客消费1000元,便可获得奖券一张,每张奖券中奖的概率为![]() ,中奖后移动公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为
,中奖后移动公司返还顾客现金1000元,小李购买一台价格2400元的手机,只能得2张奖券,于是小李补偿50元给同事购买一台价格600元的小灵通(可以得到三张奖券),小李抽奖后实际支出为![]() (元).
(元).
(1)求![]() 的分布列;
的分布列;
(2)试说明小李出资50元增加1张奖券是否划算。
18.(本小题满分12分)
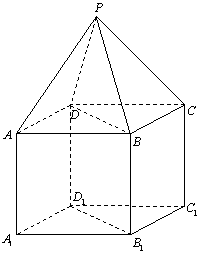
如图,![]() 是正四棱锥,
是正四棱锥,![]()
是正方体,其中![]() ,
,
(1) 求证![]() ;
;
(2) 求平面![]() 与平面
与平面![]() 所成的锐二面
所成的锐二面
角![]() 的大小;
的大小;
(3)求![]() 到平面
到平面![]() 的距离.
的距离.
19.(本小题满分12分)
甲、乙两公司同时开发同一种新产品,经测算,对于函数f(x)、g(x),当甲公司投入x万元作宣传时,若乙公司投入的宣传费小于f(x)万元,则乙公司对这一新产品的开发有失败的风险,否则没有失败的风险;当乙公司投入x万元作宣传时,若甲公司投入的宣传费小于g(x)万元,则甲公司对这一新产品的开发有失败的风险,否则没有失败的风险。
(1)试解释![]() 的实际意义;
的实际意义;
(2)设![]() ,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司各应投入多少宣传费?
20.(本小题满分13分)
已知![]() ,及直线
,及直线![]() .
.
(1)求与![]() 都外切的动圆圆心
都外切的动圆圆心![]() 的轨迹方程.并证明当
的轨迹方程.并证明当![]() 时,点
时,点![]() 到圆
到圆![]() 的圆心
的圆心![]() 的距离与
的距离与![]() 到定直线
到定直线![]() 的距离之比为一个常数;
的距离之比为一个常数;
(2) 延长![]() 与动点
与动点![]() 的轨迹交于另一点
的轨迹交于另一点![]() ,求
,求![]() 的最小值;
的最小值;
(3)若存在某一位置,使得![]() (
(![]() 仍为过
仍为过![]() 的弦)的中点
的弦)的中点![]() 在直线
在直线![]() 上的射影
上的射影![]() 满足
满足![]() ,求
,求![]() 的取值范围.
的取值范围.
21.(本小题满分14分)
已知曲线C:xy=1,过C上一点![]() 作一斜率为
作一斜率为![]() 的直线交曲线C于另一点
的直线交曲线C于另一点![]() ,点列
,点列![]() 的横坐标构成数列{
的横坐标构成数列{![]() },其中
},其中![]() 。
。
(1)求![]() 与
与![]() 的关系式;
的关系式;
(2)求证:{![]() }是等比数列;
}是等比数列;
(Ⅲ)求证:![]() 。
。
理科数学答案
一、DCDAD CBACB
二、11、![]() , 12、90, 13、
, 12、90, 13、![]() , 14、1,
, 14、1,
15、![]() (其中第一问3分,第二问2分)
(其中第一问3分,第二问2分)
![]() 三、16、①由
三、16、①由
 ②
②
17、(1)![]() 的所有可能取值为2450,1450,450,-550 ,
的所有可能取值为2450,1450,450,-550 ,
![]()
![]()
![]()
![]() ,
,![]() 分布列为
分布列为
|
| 2450 | 1450 | 450 | -550 |
| P |
|
|
|
|
…(6分)
(2)
![]()
=1850(元)) …(9分)
设小李不出资50元增加1张奖券消费的实际支出为![]() (元)
(元)
则![]()
![]()
![]()
∴![]()
∴![]()
故小王出资50元增加1张奖券划算。…(12分)
18、以![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴建立空间直角坐标系.
轴建立空间直角坐标系.
(1)设![]() 是
是![]() 的中点,
的中点,![]() 是正四凌锥,
是正四凌锥,![]() ,又
,又![]()
![]()
即![]() ;。。。。。。。。4分
;。。。。。。。。4分
(2)设平面![]() 的法向量是
的法向量是![]() ,
,![]() ,
,
![]() ,取
,取![]() 得
得![]() ,又因平面
,又因平面![]() 的
的
法向量是![]() ;
;
。。。。。。8分
(3)![]() 到平面
到平面![]() 的距离
的距离![]() 。。。。。12分
。。。。。12分
19、解:(1)f(0)=10表示当甲公司不投入宣传费时,乙公司要避免新产品的开发有失败风险,至少要投入10万元宣传费;g(0)=20表示当乙公司不投入宣传费时,甲公司要避免新产品的开发有失败的风险,至少要投入20万元宣传费。………………………………4分
(2)设甲公司投入宣传费x万元,乙公司投入宣传费y万元,依题意,当且仅当
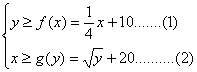 成立,双方均无失败的风险……………………8分
成立,双方均无失败的风险……………………8分
由(1)(2)得![]()
![]()
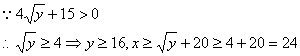
![]()
答:要使双方均无失败风险,甲公司至少要投入24万元,乙公司至少要投入16万元。
……………………………………………………………………………………12元
20、(1)由题意,
![]()
![]() 。。。。。。3分
。。。。。。3分
![]() 为右准线,
为右准线,![]() 为右焦点,
为右焦点,
![]() 到
到![]() 的距离与到直线
的距离与到直线![]() 的距离之比为常数
的距离之比为常数![]() 。。。。。。 5分
。。。。。。 5分
(2)![]()
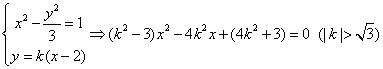
![]()
(![]() 与
与![]() 轴垂直时取最小值)。。。。。。。。。。。9分
轴垂直时取最小值)。。。。。。。。。。。9分
(3)由![]() ,则
,则![]()
![]()
又当![]() 不存在时,即
不存在时,即![]() 与
与![]() 轴垂直,此时
轴垂直,此时![]() ,
,
由此可知:![]() 。。。。。。。。。。13分
。。。。。。。。。。13分
21.解:(1)过C:![]() 上一点
上一点![]() 作斜率为
作斜率为![]() 的直线交C于另一点
的直线交C于另一点![]() ,
,
则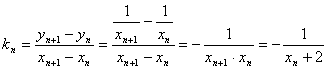 ,
,
于是有:![]() 。 …………….5分
。 …………….5分
(2)记![]() ,则
,则
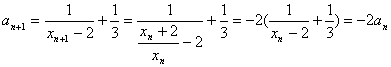 ,
,
因为![]() ,
,
因此数列{![]() }是等比数列。 ……………10分
}是等比数列。 ……………10分
(3)由(2)可知: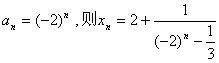 ,
,
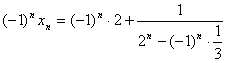 。
。
当n为偶数时有:
![]()
=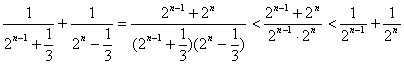 ,
,
于是
①在n为偶数时有:
![]() 。
。
②在n为奇数时,前n-1项为偶数项,于是有:
![]()
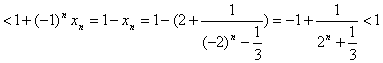 。
。
综合①②可知原不等式得证。 …………..14分