高三理科数学第一次月考试卷
命题人 胡海
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知![]() ,
, ![]() ,则条件
,则条件![]() 是条件
是条件![]() 的( )
的( )
 (A)充分不必要条件
(B)必要不充分条件
(A)充分不必要条件
(B)必要不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
2.某赛季,甲、乙两名篮球运动员都参加了11场比赛,他们每场比
赛得分的情况用如右图所示的茎叶图表示,则甲、乙两名运动员
的中位数分别为( )
A.19、13 B.13、19
C.20、18 D.18、20
3.已知函数![]() ,集合
,集合![]() ,现从A中任取两个不同的元素m,n,则
,现从A中任取两个不同的元素m,n,则![]() 的概率为( )
的概率为( )
A. ![]() B.
B. ![]() C.
C.
![]() D.
D.
![]()
4.已知![]() ,则
,则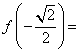 (
)
(
)
 A.-1 B.
A.-1 B.![]() C.0
D.
C.0
D.![]()
5.已知向量![]() ,
,![]() ,若
,若![]() ,
,
则![]() (
)
(
)
A.![]() B.
B.![]() C.1
D.3
C.1
D.3
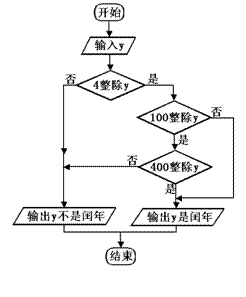
6.如右图所示,是关于判断闰年的流程图,则以
下年份是闰年的为( )
A.1996年
B.1998年
C.2010年
D.2100年
7.在△ABC中,![]() 、
、![]() 、
、![]() 分别是角
分别是角![]() 所对的边,
所对的边,![]() 60º,
60º,![]() ,△
,△![]() 的面积
的面积![]() =
=![]() ,则
,则![]() 的值等于( )
的值等于( )
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
8.在数列![]() 中,
中,![]() ,
, ![]() ,则
,则![]() ( )
( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
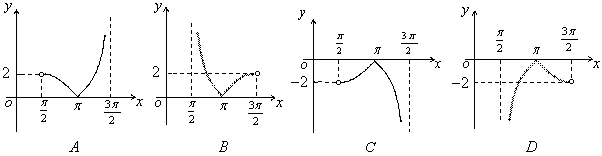 9.函数
9.函数![]() 在区间
在区间![]() 内的图象是( )
内的图象是( )
10.将函数![]() 的图象F按向量
的图象F按向量![]() 平移得到图象
平移得到图象![]() ,若
,若![]() 的一条对称轴是直线
的一条对称轴是直线![]() ,则
,则![]() 的一个可能取值是( )
的一个可能取值是( )
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
11.若双曲线![]() (a>0,b>0)上横坐标为
(a>0,b>0)上横坐标为![]() 的点到右焦点的距离大于它到左准线的距离,则双曲线离心率的取值范围是( )
的点到右焦点的距离大于它到左准线的距离,则双曲线离心率的取值范围是( )
 A.(1,2)
B.(2,+
A.(1,2)
B.(2,+![]() ) C.(1,5)
D. (5,+
) C.(1,5)
D. (5,+![]() )
)
12.如图,已知平行六面体![]() 的六个面都是菱形,则
的六个面都是菱形,则![]() 在面
在面![]() 上的射影是
上的射影是![]() 的( )
的( )
(A)重心 (B)外心
(C)内心 (D)垂心
二.填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卡的相应位置.
13.已知曲线C:![]() ,则在x=0处切线方程为
。
,则在x=0处切线方程为
。
14.已知![]() 则
则![]() 的最小值是
。
的最小值是
。
15. 已知函数![]() ,
,![]() ,直线
,直线![]() 与
与![]() 的图像分别交于
的图像分别交于![]() 、
、![]() 两点,则
两点,则![]() 的最大值是 .
的最大值是 .
16.给出下列四个结论:
①函数![]() 在其各自
在其各自
定义域上具备相同单调性;
②函数![]() 为非零常数)的图象可由函数y=3x的图象经过平移得到;
为非零常数)的图象可由函数y=3x的图象经过平移得到;
③函数![]() 是偶函数;
是偶函数;
④函数y=cosx是周期函数.
其中正确结论的序号是 .(填写你认为正确的所有结论序号)
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
17.(本小题满分12分)
 某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段
某校从参加高一年级期末考试的学生中抽出60名学生,将其成绩(均为整数)分成六段![]() ,
,![]() …
…![]() 后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求第四小组的频率,并补全这个频率分布直方图;
(Ⅱ)估计这次考试的及格率(60分及以上为及格)和
平均分;
(Ⅲ) 从成绩是70分以上(包括70分)的学生中选两人,
求他们在同一分数段的概率.
18.(本小题满分12分)
在平面直角坐标系中,O为坐标原点,A、B、C三点满足![]()
(Ⅰ)求证:A、B、C三点共线;
(Ⅱ)已知![]() ,
,![]() 的最小值为
的最小值为![]() ,求实数
,求实数![]() 的值.
的值.
19.(本小题满分12分)
设数列![]() 的前
的前![]() 项和
项和![]() ,
,![]() 为等比数列,且
为等比数列,且![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() ,求数列
,求数列![]() 前
前![]() 项和
项和![]() .
.
20.(本小题满分12分)
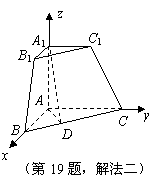
三棱锥被平行于底面![]() 的平面所截得的几何体如图所示,截面为
的平面所截得的几何体如图所示,截面为![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
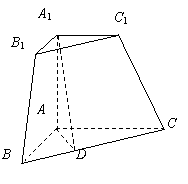 (Ⅰ)证明:平面
(Ⅰ)证明:平面![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
21.(本小题满分12分)
在直角坐标系![]() 中,点P到两点
中,点P到两点![]() ,
,![]() 的距离之和等于4,设点P的轨迹为
的距离之和等于4,设点P的轨迹为![]() ,直线
,直线![]() 与C交于A,B两点.
与C交于A,B两点.
(Ⅰ)写出C的方程;
(Ⅱ)若![]()
![]()
![]() ,求k的值;
,求k的值;
(Ⅲ)若点A在第一象限,证明:当k>0时,恒有![]() >
>![]() .
.
22.(本小题满分14分)
已知二次函数![]() 为常数);
为常数);![]() .若直线
.若直线![]() 1、
1、![]() 2与函数f(x)的图象以及
2与函数f(x)的图象以及![]() 1,y轴与函数f(x)的图象所围成的封闭图形如阴影所示.
1,y轴与函数f(x)的图象所围成的封闭图形如阴影所示.
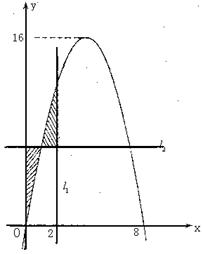 (Ⅰ)求
(Ⅰ)求![]() 、b、c的值
、b、c的值
(Ⅱ)求阴影面积S关于t的函数S(t)的解析式;
(Ⅲ)若![]() 问是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
问是否存在实数m,使得y=f(x)的图象与y=g(x)的图象有且只有两个不同的交点?若存在,求出m的值;若不存在,说明理由.
2008--2009年度六安一中第一次月考数学(理)试卷答案
一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1. A 2.A 3. A 4. D 5. D 6. A
7. C 8. A 9. D 10. A. 11. B 12. D
二.填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卡的相应位置.
13. 2x-y+1=0 14.4 15. ![]() 16. ③④
16. ③④
三、解答题:本大题共6小题,共74分.解答应写出文字说明、证明过程或演算步骤.
 17.(本题满分12分)
17.(本题满分12分)
(Ⅰ)因为各组的频率和等于1,故第四组的频率:
![]() …2分
…2分
直方图如右所示……………………………….4分
(Ⅱ)依题意,60及以上的分数所在的第三、四、五、六组,
频率和为 ![]()
所以,抽样学生成绩的合格率是![]() %..................................6分
%..................................6分
利用组中值估算抽样学生的平均分
![]() ………….8分
………….8分
=![]()
=71
估计这次考试的平均分是71分………………………………………….9分
(Ⅲ)![]() ,
,![]() ,
,![]() ”的人数是18,15,3。所以从成绩是70分以上(包括70分)的学生中选两人,他们在同一分数段的概率。
”的人数是18,15,3。所以从成绩是70分以上(包括70分)的学生中选两人,他们在同一分数段的概率。
![]()
![]() ……………………………………………………12分
……………………………………………………12分
18.(本小题满分12分).
解(Ⅰ)![]() ,
,
![]()
![]() 3分
3分
![]() 三点共线
……………………………………………4分
三点共线
……………………………………………4分
(Ⅱ)由![]()
![]() ……………………………5分
……………………………5分
![]() ,故
,故![]() …………………………………6分
…………………………………6分
从而![]()
![]()
![]() ………………………………………10分
………………………………………10分
又![]() ,
,![]() 当
当![]() 时,
时,![]() 取最小值.
取最小值.
即![]() …………………………………………………11分
…………………………………………………11分
![]() ,
,![]() ………………………………………………12分
………………………………………………12分
19.(本小题满分12分)
解:(Ⅰ)![]() 当
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,
,
故![]() 的通项公式为
的通项公式为![]() 是首项为2,公差为4的等差数列.
是首项为2,公差为4的等差数列.
(Ⅱ) 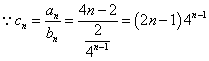 ,
,
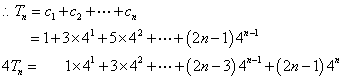
两式相减得![]()
![]()
20.(本小题满分12分)
.解法一:(Ⅰ)![]()
![]() 平面
平面![]() 平面
平面![]() ,
,
![]()
![]() .在
.在![]() 中,
中,![]() ,
,
![]() ,
,![]() ,又
,又![]() ,
,
![]() ,
,![]() ,即
,即![]() .
.
又![]() ,
,![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() .
.
(Ⅱ)如图,作![]() 交
交![]() 于
于![]() 点,连接
点,连接![]() ,
,
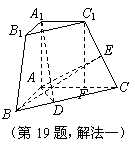 由已知得
由已知得![]() 平面
平面![]() .
.![]() 是
是![]() 在面
在面![]() 内的射影.
内的射影.
由三垂线定理知![]() ,
,![]() 为二面角
为二面角![]() 的平面角.
的平面角.
过![]() 作
作![]() 交
交![]() 于
于![]() 点,
点,
则![]() ,
,![]() ,
,![]() .
.
在![]() 中,
中,![]() .
.
 在
在![]() 中,
中,![]() .
.![]() ,
,
即二面角![]() 为
为![]() .
.
解法二:(Ⅰ)如图,建立空间直角坐标系,
则![]() ,
,
![]() ,
,![]() .
.
![]() 点坐标为
点坐标为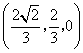 .
.![]()
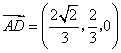 ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)![]() 平面
平面![]() ,取
,取![]() 为平面
为平面![]() 的法向量,
的法向量,
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() .
.
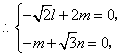
![]() ,
,
如图,可取![]() ,则
,则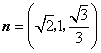 ,
,
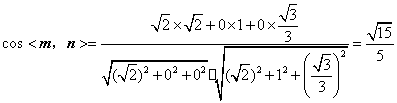 ,
,
即二面角![]() 为
为![]() .
.
21.(本小题满分12分)
解:(Ⅰ)设P(x,y),由椭圆定义可知,点P的轨迹C是以![]() 为焦点,长半轴为2的椭圆.它的短半轴
为焦点,长半轴为2的椭圆.它的短半轴![]() ,
,
故曲线C的方程为![]() .··················································································· 3分
.··················································································· 3分
(Ⅱ)设![]() ,其坐标满足
,其坐标满足
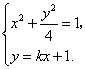 消去y并整理得
消去y并整理得![]() ,
,
故![]() .······································································· 5分
.······································································· 5分
若![]() ,即
,即![]() . 而
. 而![]() ,
,
于是![]() ,
,
化简得![]() ,所以
,所以![]() .············································································ 8分
.············································································ 8分
(Ⅲ)![]()
![]()
![]()
![]() .
.
因为A在第一象限,故![]() .由
.由![]() 知
知![]() ,从而
,从而![]() .又
.又![]() ,
,
故![]() ,
,
即在题设条件下,恒有![]() .··········································································· 12分
.··········································································· 12分
22.(本小题满分14分)
解:(I)由图形可知二次函数的图象过点(0,0),(8,0),并且f(x)的最大值为16
则 ,
,
∴函数f(x)的解析式为![]() …………………………4分
…………………………4分
(Ⅱ)由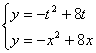 得
得![]()
∵0≤t≤2,∴直线l1与f(x)的图象的交点坐标为(![]() …………………6分
…………………6分
由定积分的几何意义知:
![]()
![]()
![]() ………………………………9分
………………………………9分
(Ⅲ)令![]()
因为x>0,要使函数f(x)与函数g(x)有且仅有2个不同的交点,则函数
![]() 的图象与x轴的正半轴有且只有两个不同的交点
的图象与x轴的正半轴有且只有两个不同的交点
![]()
∴x=1或x=3时,![]()
当x∈(0,1)时,![]() 是增函数;
是增函数;
当x∈(1,3)时,![]() 是减函数
是减函数
当x∈(3,+∞)时,![]() 是增函数
是增函数
∴![]()
![]() …………12分
…………12分
又因为当x→0时,![]() ;当
;当![]()
所以要使![]() 有且仅有两个不同的正根,必须且只须
有且仅有两个不同的正根,必须且只须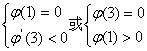
即![]() , ∴m=7或
, ∴m=7或![]()
∴当m=7或![]() 时,函数f(x)与g(x)的图象有且只有
时,函数f(x)与g(x)的图象有且只有
两个不同交点。……………………………14分