2009届高三理科数学第一次模拟考试
数学试题（理科）
注 意 事 项
考生在答题前请认真阅读本注意事项及各题答题要求
1．本试卷共4页，包含填空题(共14题)、解答题(共6题)，满分160分，考试时间为120分钟。
2．答题前，请您务必将自己的姓名、考试证号用书写黑色字迹的0.5毫米签字笔填写在答题纸上。
3．请认真核对答题纸密封线内规定填写的项目是否准确。
4．作答试题必须用书写黑色字迹的0.5毫米签字笔写在答题纸上的指定位置，在其他位置作答一律无效．如有作图需要，可用2B铅笔作答，并请加黑加粗，描写清楚。
一、填空题：本大题共14题，每小题5分，共70分，请将正确答案填写在答题纸的相应位置．
1．设
，集合
，则
▲ ．
2．幂函数
的图象经过点
，则的解析式是 ▲
．
3．
= ▲ ．
4．设f(x)是奇函数，且当x>0时，f(x)=
,则当x<0时，f(x)= ▲ ．
5．若
,且
,则
的值等于 ▲ ．
6．
则
的元素个数为 ▲ ．
7．已知函数
是偶函数，并且对于定义域内任意的
，满足
，
若当
时，
，则
= ▲ ．
8．若一系列函数的解析式相同，值域相同，但其定义域不同，则称这些函数为“同族函数”，那么函数解析式为
,值域为
的“同族函数”共有 ▲ 个．
9．若
，
，
，
，则
的大小关系是 ▲ ．
（请用“＜”号连接）
10．已知集合
等于▲ ．
11．已知函数
的图象恒过定点
，若点在直线
上，其中
，则
的最小值为 ▲ ．
12．将全体正整数排成一个三角形数阵：
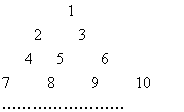
按照以上排列的规律，第
行
从左向右的第3个数为 ▲ .
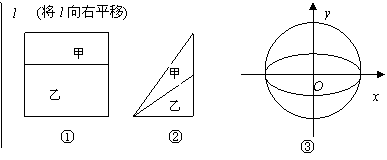
13．我们可以运用下面的原理解决一些相关图形的面积问题：如果与一固定直线平行的直线被甲、乙两个封闭的图形所截得线段的比都为k，那么甲的面积是乙的面积的k倍.你可以从给出的简单图形①、②中体会这个原理.现在图③中的曲线分别是
与
，运用上面的原理，图③中椭圆的面积为 ▲ ．
14对，记
，函数
的最大值为 ▲ ．
二、解答题：本大题共6小题；共90分．解答应写出文字说明、证明过程或演算步骤．
15．（本小题满分14分）
集合A=｛1，3，a｝，B=｛1，a2｝，问是否存在这样的实数a，使得B
A，
且A∩B=｛1，a｝？若存在，求出实数a的值；若不存在，说明理由．
16．（本小题满分14分）
已知f (x)＝
(a>0, a≠1)
（1）求f (x)的定义域；
（2） 判断f (x)的奇偶性并给予证明；
（3）求使f (x)>0的x的取值范围．
17．（本小题满分14分）
设命题
函数
是
上的减函数，命题
函数
在
的值域为
．若“
且
”为假命题，“或”为真命题，求
的取值范围．
18．（本小题满分16分）
设函数
求证：
（1）
；
（2）函数在区间（0，2）内至少有一个零点；
（3）设
是函数的两个零点，则
19．（本小题满分16分）
已知f(x)=lnx－x2+bx+3
（1）若函数f(x)在点（2，y）处的切线与直线2x+y+2=0垂直，求函数f(x)在区间[1，3]上的最小值；
（2）若f(x)在区间[1，m]上单调，求b的取值范围.
20．(本小题满分16分)
设
，
为常数）．当
时，
，且
为上的奇函数．
（Ⅰ）若
，且的最小值为
，求的表达式；
（Ⅱ）在（Ⅰ）的条件下，
在
上是单调函数，求
的取值范围．
通州市三余中学2009届高三第一次模拟考试
数学试题（理科）
参考答案及评分标准
一、填空题：本大题共14题，每小题5分，共70分，请将正确答案填写在答题纸的相应位置．
1．设，集合，则 ▲ ．2
2．幂函数的图象经过点，则的解析式是 ▲
．
3．= ▲ ．2
4．设f(x)是奇函数，且当x>0时，f(x)=,则当x<0时，f(x)= ▲ ．f(x)=
5．若,且,则的值等于 ▲ ．
6．则的元素个数为 ▲ ． 0
7．已知函数是偶函数，并且对于定义域内任意的，满足，
若当时，，则= ▲ ．
8．若一系列函数的解析式相同，值域相同，但其定义域不同，则称这些函数为“同族函数”，那么函数解析式为,值域为的“同族函数”共有 ▲ 个． 9
9．若，，，，则的大小关系是 ▲ ．
（请用“＜”号连接）
10．已知集合等于▲ ．
11．已知函数的图象恒过定点，若点在直线
上，其中，则的最小值为 ▲ ．8
12．将全体正整数排成一个三角形数阵：
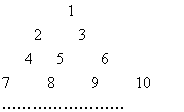
按照以上排列的规律，第行从左向右的第3个数为 ▲ . 
13．我们可以运用下面的原理解决一些相关图形的面积问题：如果与一固定直线平行的直线被甲、乙两个封闭的图形所截得线段的比都为k，那么甲的面积是乙的面积的k倍.你可以从给出的简单图形①、②中体会这个原理.现在图③中的曲线分别是与，运用上面的原理，图③中椭圆的面积为 ▲ ．
ab
14对，记，函数 的最大值为 ▲ ．1
二、解答题：本大题共6小题；共90分．解答应写出文字说明、证明过程或演算步骤．
15．（本小题满分14分）
集合A=｛1，3，a｝，B=｛1，a2｝，问是否存在这样的实数a，使得BA，
且A∩B=｛1，a｝？若存在，求出实数a的值；若不存在，说明理由．
解：由A=｛1，3，a｝，B=｛1，a2｝，BA，得a2=3．或a2=a．
当a2=3时，
，此时A∩B≠｛1，a｝；
7′
当a2=a时，a=0或a=1， 9′
a=0时，A∩B=｛1，0｝； 11′
a=1时，A∩B≠｛1，a｝． 13′
综上所述，存在这样的实数a=0，使得BA，且A∩B=｛1，a｝． 14′
16．（本小题满分14分）
已知f (x)＝ (a>0, a≠1)
（1）求f (x)的定义域；
（2） 判断f (x)的奇偶性并给予证明；
（3）求使f (x)>0的x的取值范围．
解：(1) 由
＞0，解得x ∈（–1，1）．
4′
(2) f
(－x)＝
＝－f (x),
且x∈（－1，1）
∴函数y＝f (x)是奇函数． 8′
(3)若a>1, f
(x)>0则＞1， 解得0<x<1；
11′
若0<a<1,
f (x)>0则0＜＜1，解得－1<x<0,.
14′
17．（本小题满分14分）
设命题函数是上的减函数，命题函数
在的值域为．若“且”为假命题，“或”为真命题，求的取值范围．
解：由
得
………………………………………………3分
，在
上的值域为
得
……………7分
且为假，或为真 得、中一真一假．
若真假得， 
……………………………10分
若假真得，
．
………………………………………………12分
综上，或
． ………………………………………………14分
18．（本小题满分16分）
设函数求证：
（1）；
（2）函数在区间（0，2）内至少有一个零点；
（3）设是函数的两个零点，则
证明：（1）
2′
又
又2c=－3a－2b 由3a＞2c＞2b ∴3a＞－3a－2b＞2b
∵a＞0 
6′
（2）∵f（0）=c，f（2）=4a+2b+c=a－c
①当c＞0时，∵a＞0，∴f（0）=c＞0且
∴函数f（x）在区间（0，1）内至少有一个零点 9′
②当c≤0时，∵a＞0 
∴函数f（x）在区间（1，2）内至少有一个零点.
综合①②得f（x）在（0，2）内至少有一个零点 11′
（3）∵x1，x2是函数f（x）的两个零点
则
的两根
∴
16′
19．（本小题满分16分）
已知f(x)=lnx－x2+bx+3
（1）若函数f(x)在点（2，y）处的切线与直线2x+y+2=0垂直，求函数f(x)在区间[1，3]上的最小值；
（2）若f(x)在区间[1，m]上单调，求b的取值范围.
解：（1）
直线2x+y+2=0 斜率为－2
令f′(2)= 
得b=4
3′
f(x)=lnx－x2＋4x＋3
5′
| x | 1 | (1, |
| （ | 3 |
| y′ | + | 0 | － | ||
| y | 6 |
| 极大 |
| 6＋ln3 |
)
因为6+ln3>6 ∴x=1时 f(x)在[1，3]上最小值6. 8′
（2）令≥0得b≥2x－，在[1，m]上恒成立而
y=2x－在[1，m]上单调递增，最大值为2m－
∴b≥2m－
12′
令≤0 得b≤2x－，在[1，m]上恒成立
而 y=2x－在[1，m] 单调递增，最小值为y=1
∴b≤1
故b≥2m－ 或b≤1时f(x)在[1，m]上单调．
16′
20．(本小题满分16分)
设，为常数）．当时，，且为上的奇函数．
（Ⅰ）若，且的最小值为，求的表达式；
（Ⅱ）在（Ⅰ）的条件下，在上是单调函数，求的取值范围．
(1)解:
由得
,
………………………………………………1分
若
则
无最小值.
. ………………………………………2分
欲使取最小值为0,只能使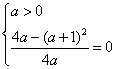
,昨
,
.
………………………………………………4分
得
则
,
又
,
………………………7分
又
………………………………………………8分
………………………………9分
(2)
.
.
得
.则
,
.………………………………………………12分
当
,或
或
时,
为单调函数.
综上,
或
.
……………………………………………16分
通州市三余中学2009届高三第一次模考答案纸
数学试题（理科）
一．填空题：(本大题共14小题，每小题
分，共70分．请把结果直接填在题中横线上)
1. __________________ 2. ___________________________
3. __________________ 4. ___________________________
5. __________________ 6. ___________________________
7. __________________ 8. ___________________________
9. __________________ 10. __________________________
11. _________________ 12. __________________________
13. _________________ 14. __________________________
二．解答题：(本大题共6小题，共90分．解答应写出文字说明、证明过程或演算步骤.)
15.
16.
17.
18.
19．
20.