高三第一轮复习训练题
数学（十九）（理科·极限）
一、选择题：本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的。
1．
,则a的值为
A．1
B．
C．0 D．－1
2．若
是定义在R上的连续函数，且
，则
A．2 B．1 C．0 D．
3.已知数列1，2，2，3，3，3，4，4，4，4。。。。。。则这个数列的第2006个数是
A 62 B。63 C 64 D 65
4．设f(x)=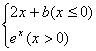
若
f(x)存在，则常数b为
A 0 B 1 C 2 D e
5．已知正数a、b满足a+b=2，n
N+，则
=
A．a B．b C．0 D．不存在
6.函数f（x）=
的不连续点为
A x=
B x=1
C x=
D 以上答案都不对
7用数学归纳法证明命题时，此命题左式为
，则n=k+1与n=k时相比，左边应添加
A．
B．
C．
D．
8已知
，下面结论正确的是
A．
在
处连续 B．
C．
D．
9用数学归纳法证明（n+1）(n+2)(n+3)…..(n+n)=
·1·3….(2n+1) (n
)时，从n=k到n=k+1时，左边需要增乘的代数式是
A
2k+1
B 
C 2k-1 D 
10. 数列{an}中，a1=1,Sn
是前n项和.当n≥2时，an=3Sn,则
的值是
A．－
B．－2
C．1
D．－
11. 在等差数列{an}中，a1＝
，第10项开始比1大，记t＝
，则t的取值范围是
A．t>
B．
C．
D．
12.若
(
)=9 则实数a等于
A 
B 
C 
D 
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题：本大题共4小题；每小题4分，共16分，把答案填在题中的横线上
13 等比数列
的首项a
=3, 前n项和为S
,若
=
则
=___________
14已知函数f (x)在区间
上连续，当
，则f (0)
= .
15用数学归纳法证
的过程中，当n=k到n=k+1时，左边所增加的项为_______________
16设常数
，
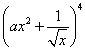展开式中
的系数为
，则
________
三、解答题：本大题共6小题，共74分，解答应写出文字说明，证明过程或推演步骤。
17
求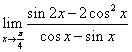
18
已知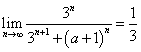
，求a 的取值范围.
19. 已知递增等比数列{an}满足：a2+a3+a4＝28且a3+2是a2和a4的等差中项，
⑴求数列{an}的通项公式；
⑵若
，Sn＝b1＋b2＋…＋bn，求
20.数列
（1）求
（2）证明猜想的正确性
21.函数
的定义域为R，且
（1）求证：
（2）若
上的最小值为
，
求证：
.
22.已知数列
R）对于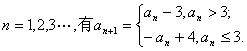
（I）当
（II）若a满足
，求数列
的通项
；
（III）证明：满足≤3的自然数n存在.
2007－2008学年度范水高级中学高三第一轮复习训练题
高三第一轮复习训练题
数学（十九）（理科·极限）参考答案
一.1. C 2. C 3.B 4.B 5. C, 6.A 7.C 8.D 9.B 10. A 11. D 12.B
二.13.
2 14 . 
15 . 
16. 1
三.17 解
18 解：依题意有：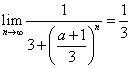
19. 解：（1）设公比为
，则
。
据题意得：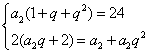
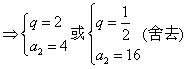
所以
（2）因为
所以
故
20 解： 
同理得，
猜想
（2）证明：n=1时，
假设n=k 时，猜想正确，即
又
即n=k+1时也成立
21.解 ⑴
定义域为R，
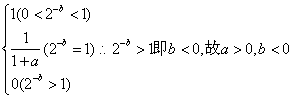
⑵由⑴知
22. 解：（I）
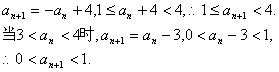
因此，
（II）
∴猜想对于任意正整数l有
下面用数学归纳法证明对
（i）
满足对
（ii）假设当
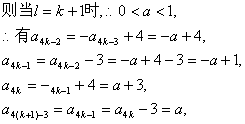
由（i）（ii）可知对任意
同理可证
（III）假设对所有的n，
，
知数列是首项为a，公差为－3的等差数列.
对于充分大的n，会有
，这与假设矛盾，
∴假设错误，
∴有满足的自然数n存在