高三理科数学第一轮复习训练题
数学(二十一) (理科![]() 综合卷1)
综合卷1)
一、选择题:本大题共有12个小题,每小题5分,共60分。每小题给出的四个选项中,只有一项是符合要求的。
1.设集合![]() =
=
A.{1,2} B.{-1,3} C.{1}或{2} D.![]()
2. 抛物线![]() 的焦点坐标是
的焦点坐标是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.随机变量![]() ,记
,记![]() ,则下列式子中错误的是
,则下列式子中错误的是
A.![]() B.
B. ![]()
C.![]() D.
D.![]()
4.对于直线m.n和平面α,下面命题中的真命题是( )
![]()
![]()
![]()
![]()
5.若不等式![]() 对于一切
对于一切![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围
的取值范围
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
6.已知复数![]() =
=
A.1-i B.1-3i C.1+i D.3-3i
7.直线![]() 的倾斜角是
的倾斜角是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8.按ABO血型系统学说,每个人的血型为A,B,O,AB型四种之一,依血型遗传学,当且仅当父母中至少有一人的血型是AB型时,子女的血型一定不是O型,若某人的血型是O型,则其父母血型的所有可能情况有
A.12 B.10 C.9 D.6
9.若![]() 的展开式中各项系数和为
的展开式中各项系数和为![]() ,
,![]() 的展开式各项系数之和为
的展开式各项系数之和为![]() ,则
,则![]() 等于
等于
A.1
B.-1
C.![]() D.
D.![]()
10.一个球与一个正三棱柱的三个侧面和两个底面都相切,已知这个球的体积为![]() ,那么这个正三棱柱的体积是
,那么这个正三棱柱的体积是
A.96![]() B.16
B.16![]() C.24
C.24![]() D.48
D.48![]()
11.数列![]() 是一个单调递增数列,则实数
是一个单调递增数列,则实数![]() 的取值范围是
的取值范围是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
12.已知![]() 为
为![]() 与
与![]() 中较小者,其中
中较小者,其中![]() ,若
,若![]() 的值域为
的值域为![]() ,则
,则![]() 的值是
的值是
A.0 B.![]() C.
C.![]() D.
D.![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(本大题共4小题,每小题4分,共16分,将正确答案填在试题的横线上)
13.函数![]() 的反函数是
的反函数是
14.椭圆![]() 与直线
与直线![]() 交于A、B两点,过原点与线段AB中点的直线的斜率为
交于A、B两点,过原点与线段AB中点的直线的斜率为![]() 的值为_____________
的值为_____________
15.等差数列{an}中,a1![]() a4
a4![]() a10
a10![]() a16
a16![]() a19
a19![]() 150,则
150,则![]() 的值是
的值是
16.若函数![]() 是定义在实数集上的奇函数,且
是定义在实数集上的奇函数,且![]() ,给出下列结论:
,给出下列结论:
①![]() ;②
;②![]() 以4为周期;③
以4为周期;③![]() 的图象关于
的图象关于![]() 轴对称;④
轴对称;④![]() .
.
这些结论中正确的有____________(必须填写序号).
三、解答题(本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)
17.已知向量![]() ,设
,设![]()
(1)若![]() ,求
,求![]() 的值域.
的值域.
(2)若![]() 的图象可以按向量
的图象可以按向量![]() 平移后得到
平移后得到![]() 的图象,指出向量
的图象,指出向量![]() 的一个值.
的一个值.
18.在一次语文测试中,有一道把我国四大文学名著《水浒传》 《三国演义》 《西游记》 《红楼梦》与它们的作者连线的题目,每连对一个得3分,连错不得分,一位同学该题得ξ分.
(1)求该同学得分不少于6分的概率;
(2)求ξ的分布列及数学期望.
19.已知![]() 是数列
是数列![]() 的前
的前![]() 项和,
项和,![]() ,且
,且![]() ,其中
,其中![]() .
.
(1)求数列![]() 的通项公式
的通项公式![]() ; (2)计算
; (2)计算![]() 的值.
的值.
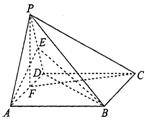
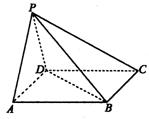 20.如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧面PAD是正三角形,且平面PAD⊥底面ABCD.
20.如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧面PAD是正三角形,且平面PAD⊥底面ABCD.
(1)求证:AB⊥平面PAD
(2)求直线PC与底面ABCD所成角的大小;
(3)设AB=1,求点D到平面PBC的距离.
21.已知直线![]() 过椭圆E:
过椭圆E:![]() 的右焦点
的右焦点![]() ,且与E相交于
,且与E相交于![]() 两点.
两点.
 (1)设
(1)设![]() (
(![]() 为原点),求点
为原点),求点![]() 的轨迹方程;
的轨迹方程;
(2)若直线![]() 的倾斜角为
的倾斜角为![]() ,求
,求![]() 的值.
的值.
22.已知关于![]() 的方程
的方程![]() 的两个根为
的两个根为![]() ,设函数
,设函数![]() .
.
(1)判断![]() 在
在![]() 上的单调性;
上的单调性;
(2)若![]() ,证明
,证明![]() .
.
2008-2009学年度祁东二中高三第一轮复习训练题
数学(二十一) (理科![]() 综合卷1)参考答案
综合卷1)参考答案
一、选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | A | C | D | C | A | B | B | C | D | D | A | D |
二、填空题
13.f-1(x)=lnx-1 (x>0).; 14.![]() ; 15.
; 15.![]() 16.①②④;
16.①②④;
三、解答题
17. 解:①![]() .........................2分
.........................2分
![]()
![]() .............................5分
.............................5分
![]()
![]()
![]() ..................8分
..................8分
②![]() ....................10分
....................10分
可见![]() 的图象向左平移
的图象向左平移![]() 个单位可得
个单位可得![]() 的图象,即
的图象,即![]() 的一个值是
的一个值是![]() ...12分
...12分
18. 解:(1)ξ的可能取值为0,3,6,12.....................................2分
P(ξ=12)==,.....................................3分
P(ξ=6)===.....................................4分
该同学得分不少于6分的概率为
P=P(ξ=6)+P(ξ=12)= .....................................6分
(2)P(ξ=3)==,
P(ξ=0)=1---=.......................................8分
∴ξ得分布列为
| ξ | 0 | 3 | 6 | 12 |
| P |
|
|
|
数学期望为Eξ=0×+3×+6×+12×=3...........................12分
19. 解:①![]()
![]()
![]()
![]()
![]()
![]() ....................................2分
....................................2分
又![]() 也满足上式,
也满足上式,![]()
![]()
![]()
![]() (
(![]() )
)
![]() 数列
数列![]() 是公比为2,首项为
是公比为2,首项为![]() 的等比数列..................4分
的等比数列..................4分
![]()
![]() .................................6分
.................................6分
②![]()
![]()
![]()
![]() ...........................9分
...........................9分
于是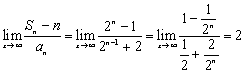 ........................12分
........................12分
20. 解法一:
(1)证明: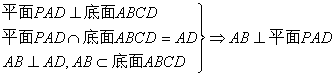 …………………2分
…………………2分
|
(2)解:取AD的中点F,连结AF,CF
∵平面PAD⊥平面ABCD,且PF⊥AD,
∴PF⊥平面BCD ………………………5分
∴CF是PC在平面ABCD上的射影,
∴所以∠PCF是直线PC与底面ABCD所成的角……………7分
在![]()
即直线PC与底面ABCD所成的角的大小是![]() ………………8分
………………8分
(3)解:设点D到平面PBC的距离为h,
![]() ………………10分
………………10分
在△PBC中,易知PB=PC=![]()
![]()
又![]()
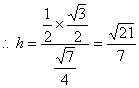 ………………11分
………………11分
即点D到平面PBC的距离为![]() ……………………………………12分
……………………………………12分
|
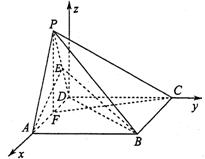
(1)证明:建立空间直角坐标系D—xyz,如图
不妨设A(1,0,0)则B(1,1,0),P(![]()
![]() ………………………2分
………………………2分
由![]()
由AB⊥AD,∴AB⊥平面PAD ………………………3分
(2)解:取AD的中点F,连结AF,CF
∵平面PAD⊥平面ABCD,且PF⊥AD,
∴PF⊥平面BCD ………………………5分
∴CF是PC在平面ABCD上的射影,
∴所以∠PCF是直线PC与底面ABCD所成的角…………………………7分
易知C(0,1,0),F(![]()
![]()
![]()
∴直线PC与底面ABCD所成角的大小为![]() ……………………8分
……………………8分
(3)解:设点D到平面PBC的距离为h,
![]() ………………10分
………………10分
在△PBC中,易知PB=PC=![]()
![]()
又![]()
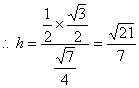 ………………11分
………………11分
即点D到平面PBC的距离为![]() ……………………………………12分
……………………………………12分
21. 解:① 设![]()
![]()
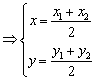 ........1分
........1分
由![]() ,易得右焦点
,易得右焦点![]() ....................2分
....................2分
当直线![]() 轴时,直线
轴时,直线![]() 的方程是:
的方程是:![]() ,根据对称性可知
,根据对称性可知![]() ......3分
......3分
当直线![]() 的斜率存在时,可设直线
的斜率存在时,可设直线![]() 的方程为
的方程为![]()
代入E有![]()
![]() ;
; ![]() ........................5分
........................5分
于是![]()
![]()
![]() ;
; ![]()
消去参数![]() 得
得![]()
而![]() 也适上式,故R的轨迹方程是
也适上式,故R的轨迹方程是![]() ...............8分
...............8分
②设椭圆另一个焦点为![]() ,
,
在![]() 中
中![]() 设
设![]() ,则
,则![]()
由余弦定理得![]()
![]() ............9分
............9分
同理,在![]() ,设
,设![]() ,则
,则![]()
也由余弦定理得![]()
![]() ............11分
............11分
于是![]() .........................12分
.........................12分
注:其它方法相应给分.
22.解:①![]() ....................3分
....................3分
由于当![]() 时
时![]() ,
,
所以![]() ,故
,故![]() 在
在![]() 上是增函数.......................6分
上是增函数.......................6分
②当![]() 时,并由①得
时,并由①得
![]() .................................7分
.................................7分
![]()
![]() .........................................9 分
.........................................9 分
![]()
![]() ...........11分
...........11分
同理![]() .........................................12分
.........................................12分
于是![]()
从而有![]() .........................................14分
.........................................14分