高三第一轮复习训练题
数学(二十二) (理科![]() 综合卷2)
综合卷2)
一、选择题:本大题共有12个小题,每小题5分,共60分。每小题给出的四个选项中,只有一项是符合要求的。
1、已知集合![]() ,
,![]() ,若
,若![]() ,则
,则![]() 等于
等于
A、1 B、2 C、1或![]() D、1或2
D、1或2
2、设复数![]() 在
在
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.设函数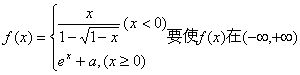 内连续,则实数a值等于
内连续,则实数a值等于
A.1 B.![]() C.
C.![]() D.
D.![]()
4.已知![]() 表示平面,m,n表示直线,则m//
表示平面,m,n表示直线,则m//![]() 的一个充分而不必要条件是
的一个充分而不必要条件是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.已知无穷数列{an}是各项均为正数的等差数列,则有
A.< B.≤ C.> D.≥
6.若函数![]() 内为增函数,则实数a的取值范围
内为增函数,则实数a的取值范围
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.设随机变量![]() 服从正态分布
服从正态分布![]() ,若
,若![]() ,则
,则![]()
A、![]() B、
B、![]() C、
C、![]() D、
D、![]()
8.已知K为实数,若双曲线![]() 的焦距与K的取值无关,则k的取值范围为
的焦距与K的取值无关,则k的取值范围为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
9.已知![]()
A.都不大于2; B.都不小于2; C.至少有一个不大于2; D.至少有一个不小于2;
10.过△ABC的重心G作一直线分别交AB、AC于D、E,若![]() ,则
,则![]() 的值为
的值为
A.1 B.2 C.3 D.4
11.设有两个独立事件A和B同时不发生的概率是P,A发生B不发生与A不发生B以生的概率相同,YC则事件A发生的概率为
A.2P
B.![]() C.
C.![]() D.
D.![]()
12.已知方程![]() 的取值范围
的取值范围
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
二、填空题(本大题共4小题,每小题4分,共16分,将正确答案填在试题的横线上)
13.若二项式(x![]() )
)![]() 展开式中的第5项是5,则x等于_________
展开式中的第5项是5,则x等于_________
14.不等式![]() 恒成立,则x的取值范围是
恒成立,则x的取值范围是
15.点P(3,1)在椭圆![]()
![]()
![]() 的
的![]() 光线经直线y=-2反射后通过椭圆的右焦点,则这个椭椭圆的离心率为
光线经直线y=-2反射后通过椭圆的右焦点,则这个椭椭圆的离心率为
16.关于函数![]() ,有下列命题
,有下列命题
①其最小正周期为![]() ; ②其图像由
; ②其图像由![]() 个单位而得到;
个单位而得到;
③其表达式写成![]() ④在
④在![]() 为单调递增函数;
为单调递增函数;
则其中真命题为
三、解答题(本大题共6小题,共74分,解答应写出文字说明、证明过程或演算步骤)
17.(本题满分12分)已知函数g(x)=![]() sin(2x+
sin(2x+![]() )的图象按向量m=(-
)的图象按向量m=(-![]() )平移得到函数
)平移得到函数
|
(1)求实数a、b的值;
(2)设函数![]() (x)=g(x)-
(x)=g(x)-![]() ,求函数
,求函数![]() (x)的单调增区间。
(x)的单调增区间。
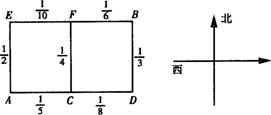 18.(本题满分12分)某人居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图.(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为
18.(本题满分12分)某人居住在城镇的A处,准备开车到单位B处上班,若该地各路段发生堵车事件都是相互独立的,且在同一路段发生堵车事件最多只有一次,发生堵车事件的概率如图.(例如:A→C→D算作两个路段:路段AC发生堵车事件的概率为![]() ,路段CD发生堵车事件的概率为
,路段CD发生堵车事件的概率为![]() )
)
(1)请你为其选择一条由A到B的最短路线(即此人只选择从西向东和从南向北的路线),使得途中发生堵车事件的概率最小;
(2)若记路线A→C→F→B中遇到堵车次数为随机变量ξ,求ξ的数学期望Eξ.
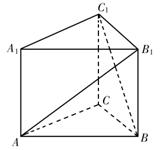
19.(本题满分12分)如图,正三棱柱ABC-A1B1C1中,底面边长为a,侧棱长为a,若经过AB1且与BC1平行的平面交上底面于DB1.
(1)试确定点D的位置,并证明你的结论;
(2)求二面角A1-AB1-D的大小.
20.(本题满分12分)已知数列![]() ,前n项的和为Sn,且4tSn+1
,前n项的和为Sn,且4tSn+1![]() 其中
其中![]()
(1)证明数列![]() 为等比数列;
(2)判定
为等比数列;
(2)判定![]() 的单调性,并证明;
的单调性,并证明;
21.(本题满分12分). 定义函数![]()
(1)求证![]()
(2)设![]()
22.(本题满分14分)直线AB过抛物线x2=2py(p>0)的焦点F,并与其相交于A、B两点,Q是线段AB的中点,M是抛物线的准线与y轴的交点,O是坐标原点.
(1)求![]() 的取值范围;
的取值范围;
(2)若p是不为1的正整数,当![]() ,△ABN的面积的取值范围为[5
,△ABN的面积的取值范围为[5![]() ,20
,20![]() ]时,求该抛物线的方程
]时,求该抛物线的方程
高三第一轮复习训练题
数学(二十二) (理科![]() 综合卷2)参考答案
综合卷2)参考答案
一 选择题:
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | D | C | A | D | B | A | B | A | D | C | C | A |
二 填空题:
13.3 14.![]() 15.
15.![]() 16. ①③④
16. ①③④
三 解答题:
17.(1)依题意按向量m平移g(x)得
f(x)-![]() =
=![]() sin[2(x+
sin[2(x+![]() )+
)+![]() ]…………………………………… 2分
]…………………………………… 2分
得f(x)=-![]() sin(2x+
sin(2x+![]() )+
)+![]() …………………………………………… 4分
…………………………………………… 4分
又f(x)=acos![]() (x+
(x+![]() )+b=-
)+b=-![]() sin(2x+
sin(2x+![]() )+
)+![]() +b
+b
比较得a=1,b=0………………………………………………………………… 6分
(2)![]() (x)=g(x)-
(x)=g(x)-![]() f(x)=
f(x)=![]() sin(2x+
sin(2x+![]() )-
)-![]() cos(2x+
cos(2x+![]() )-
)-![]()
=sin(2x+![]() )-
)-![]() ……………………………………………………… 9分
……………………………………………………… 9分
2kπ-![]() ≤2x+
≤2x+![]() ≤2kπ+
≤2kπ+![]() (k∈Z)
(k∈Z) ![]() kπ-
kπ-![]() ≤x≤kπ+
≤x≤kπ+![]() (k∈Z)
(k∈Z)
∴![]() (x)的单调增区间为[kπ-
(x)的单调增区间为[kπ-![]() ,kπ+
,kπ+![]() ](k∈Z)……………… 12分
](k∈Z)……………… 12分
18.(1)记路段MN发生堵车事件为P(MN.)
因为各路段发生堵车事件都是独立的,且在同一路段发生堵车事件最多只有一次,所以路线A→C→D→B中遇到堵车的概率P1为
1-P(![]() )=1-P(
)=1-P(![]() )·P(
)·P(![]() )·P(
)·P(![]() )
)
=1-[1-P(AC)][1-P(CD)][1-P(DB)]=1-![]() ;…………………………………3分
;…………………………………3分
同理:路线A→C→F→B中遇到堵车的概率P2为1-P(![]() )=
)=![]() (小于
(小于![]() )……4分
)……4分
路线A→E→F→B中遇到堵车的概率P3为1-P(![]() )=
)=![]() (大于
(大于![]() ) ……………5分
) ……………5分
显然要使得由A到B的路线途中发生堵车事件的概率最小,只可能在以上三条路线中选择.
因此选择路线A→C→F→B,可使得途中发生堵车事件的概率最小………………………6分
(2)路线A→C→F→B中遇到堵车次数ξ可取值为0,1,2,3. …………………………7分
P(ξ=0)=P(![]() )=
)=![]() . …………………………………8分
. …………………………………8分
P(ξ=1)=P(AC·![]() )+P(
)+P(![]() ·CF·
·CF·![]() )+P(
)+P(![]() )
)
=![]() …………………………………9分
…………………………………9分
P(ξ=2)=P(AC·CF·![]() )+P(AC·
)+P(AC·![]() ·FB)+P(
·FB)+P(![]() ·CF·FB)
·CF·FB)
![]() ………………………………… 10分)
………………………………… 10分)
P(ξ=3)=P(AC·CF·FB)=![]() ,
,
∴Eξ=0×![]() +1×
+1×![]()
答:路线A→C→F→B中遇到堵车次数的数学期望为![]() . …………………………………12分
. …………………………………12分
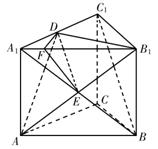 19.解: (1)D为A1C1的中点. …………………………………2分
19.解: (1)D为A1C1的中点. …………………………………2分
连结A1B与AB1交于E,
则E为A1B的中点,DE为平面AB1D与平面A1BC1的交线,
∵BC1∥平面AB1D
∴BC1∥DE,∴D为A1C1的中点. ………………………6分
(2) 解法一:过D作DF⊥A1B1于F,
由正三棱柱的性质,AA1⊥DF,∴DF⊥平面AB1,
连结EF、DE,在正三角形A1B1C1中,
∵D是A1C1的中点,∴B1D=A1B1=a,…………………7分
又在直角三角形AA1D中,
∵AD==a,∴AD=B1D. …………………………………8分
∴DE⊥AB1,∴可得EF⊥AB1,
则∠DEF为二面角A1-AB1-D的平面角. …………………………………10分
可求得DF=a,
∵△B1FE∽△B1AA1,
得EF=a,∴∠DEF=,即为所求. …………………………………12分
(2)解法(二)(空间向量法)
建立如图所示空间直角坐标系,则
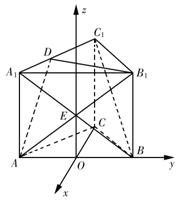 A(0,-a,0)、B1(0,a,a)、C1(-a,0,a)、
A(0,-a,0)、B1(0,a,a)、C1(-a,0,a)、
A1(0,-a,a)、D(-a,-a,a).
∴=(0,a,a),=(-a,-a,0). ……8分
设![]() =(x,y,z)是平面AB1D的一个法向量,
=(x,y,z)是平面AB1D的一个法向量,
则可得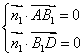 ,即
,即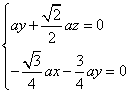 .
.
∴![]() =(-,1,-). …………………………10分
=(-,1,-). …………………………10分
又平面AB1的一个法向量
![]() ==(-a,0,0),设n1与n2的夹角是θ,
==(-a,0,0),设n1与n2的夹角是θ,
则 cosθ=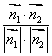 =.
=.
又可知二面角A1-AB1-D是锐角,
∴二面角A1-AB1-D的大小是. …………………………………12分
20.解(1)证明:∵ ![]() ①
①
当n=1时,4t(a1+a2)-(3t+8)a1=8t 而a1=2 ![]() ……………………… 2分
……………………… 2分
又∵![]() ②(n≥2)
②(n≥2)
由①②得![]() 即
即![]() ………………… 4分
………………… 4分
而![]() ∴{an}是等比数列……………………………………… 6分
∴{an}是等比数列……………………………………… 6分
(2)∵an=2(![]()
![]() …………………… 8分
…………………… 8分
∵t<-3 ∴![]() …………………………………………… 11分
…………………………………………… 11分
则![]() ∴{an}为递减数列…………………………………… 12分
∴{an}为递减数列…………………………………… 12分
21.解:(1)令![]() ……………………………… 1分
……………………………… 1分
![]() …………………………………………… 2分
…………………………………………… 2分
当-2<x≤0时 g’‘(x)≤0;当x>0时,g‘(x)>0………………………………… 3分
∴g(x)在(-2,0![]() 上递减,在(0,+∞)上递增…………………………………… 4分
上递减,在(0,+∞)上递增…………………………………… 4分
则x=0时 g(x)min=g(0)=0 g(x)≥g(x)min=0 ………………………………… 5分
即fn(x)≥nx ………………………………… 6分
(2)∵![]() 即
即![]() ……………………… 7分
……………………… 7分
![]() 易得x0>0 …………………………… 9分
易得x0>0 …………………………… 9分
而![]()
由(1)知x>0时(1+x)n>1+nx 故2n+1=(1+1)n+1>n+2 ∴x0<1 ………… 11分
综上0<x0<1 …………………………………………… 12分
22.解:(1)由条件得M(0,-![]() ),F(0,
),F(0,![]() ).
).
设直线AB的方程为:y=kx+![]() ,A(
,A(![]() ,
,![]() ),B(
),B(![]() ,
,![]() )
)
则![]() ,
,![]() ,Q(
,Q(![]() ).…………………………………… 1分
).…………………………………… 1分
由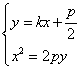 得
得![]() .…………………………………………… 3分
.…………………………………………… 3分
∴由韦达定理得![]() +
+![]() =2pk,
=2pk,![]() ·
·![]() =-
=-![]() …………………………………… 4分
…………………………………… 4分
从而有![]()
![]() =
=![]()
![]() +
+![]() =k(
=k(![]() +
+![]() )+p=
)+p=![]() .……………… 5分
.……………… 5分
![]() ·
·![]()
![]()
∴![]() ·
·![]() 的取值范围是
的取值范围是![]() …………………………………………… 7分
…………………………………………… 7分
(2)由![]() .又根据(1)知
.又根据(1)知![]()
∴4p![]() =p
=p![]() k
k![]() ,而p>0,∴k
,而p>0,∴k![]() =4,k=±2. ……………………………………… 8分
=4,k=±2. ……………………………………… 8分
由于![]() =(-pk,p),
=(-pk,p),![]()
∴![]()
从而![]() .…………………………………………… 10分
.…………………………………………… 10分
又![]() =
=![]() ,
,![]() =
=![]()
∴![]() .………………………………… 11分
.………………………………… 11分
而![]() 的取值范围是[5
的取值范围是[5![]() ,20
,20![]() ].
].
∴5![]() ≤5
≤5![]() p2≤20
p2≤20![]() ,1≤p2≤4. …………………………………………… 12分
,1≤p2≤4. …………………………………………… 12分
而p>0,∴1≤p≤2.
又p是不为1的正整数.
∴p=2.
故抛物线的方程:x2=4y. …………………………………………… 14分