高三理科数学精编模拟题 (理科一)
编审者：揭阳市教育局教研室 黄开明
编者按：该试题与本学期的3套综合训练题、调考、一模、二模试题组成一个整体，8套试题覆盖了高中数学的主要知识和方法，对重点知识既各有所侧重，又互相补充，希望同学们练后在考前能进行一次全面疏理、回归总结，力争通过疏理、总结，进一步认识自己的实力和水平，并以清醒的头脑，镇定的心态迎接高考的挑战。
一．选择题：本大题共8小题，每小题5分，共40分.在每小题给出的四个选项中，只有一项是符合题目要求的
1．复数
的虚部为
. 4 
.—4 
. 
. 
2．如图，将网格中的三条线段沿网格线上下或左右平移，组成一个首尾相连的三角形，则三条线段一共至少需要移动D
A．12格 B．11格 C．10格 D．9格
3．已知
上是单调增函数，则a的最大值是
A．0 B．1 C．2 D．3
4．对任意实数
、
，定义运算
，则
A.
B.
C. 
D.
5．已知函数
，若
，则
与
在同一坐标系内的图象可能是
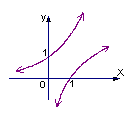
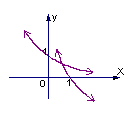
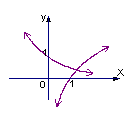
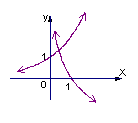
A. B. C. D.
6．设O为坐标原点，F为抛物线
的焦点，A为抛物线上的一点，若
，则点A的坐标为
A．（2，2
） B．（1，±2） C．（1，2） D．（2，
）
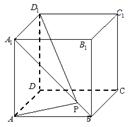7．如图所示，在棱长为1的正方体
的面对角线
上存在
一点
使得
取得最小值，则此最小值为
A. 
B. 
C. 
D. 
8．已知
，
是的零点，且
，则实数a、b、m、n的大小关系是
A．
B．
C．
D．
二、填空题：本大题共6小题，每题5分，共30分．
必做题：第9、10、11、12题是必做题，每道试题考生都必须做答．
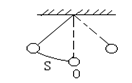
9．如右图，单摆从某点开始来回摆动，离开平衡位置O的距离S厘米和时间
秒的
函数关系为：
，那么单摆来回摆动一次所需的时间为
秒．
10．已知：
，则函数
的最大值为
.
11．记者要为5名奥运志愿者和他们帮助的2位国外奥运选手拍照，要求排成一排，2位选手要求相邻但不排在两端，不同的排法共有 ．(用数字作答)
12．对于实数
，用
表示不超过的最大整数，如
，
．若
为正整数，
，
为数列
的前项和，则
、
__________．
选做题：第13、14、15题是选做题，考生只能选做二题，三题全答的，只计算前二题的得分．
13．已知实数
满足
则
的最小值是
.
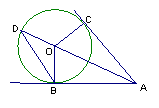
14．如图所示，AC和AB分别是圆O的切线， 且OC = 3，AB = 4，延长AO
到D点，则△ABD的面积是___________．
15．在直角坐标系
中，已知曲线的参数方程是
（
是参数），若以
为极点，轴的正半轴为极轴，则曲线的极坐标方程可写为________________.
三．解答题：本大题共6小题，共80分，解答应写出文字说明、证明过程或演算步骤.
16．（本小题满分12分）
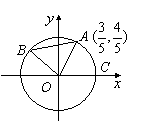
如图
、
是单位圆
上的动点，
是圆与
轴正半轴的交点，设
．
（1）当点的坐标为
时，求
的值；
（2）若
，且当点A、B在圆上沿逆时针方向移动时，总有
，试求
的取值范围．
17.（本小题满分14分）
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 0.16 | |
| 70.5~80.5 | 10 | |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | ||
| 合计 | 50 |
为了让学生了解环保知识，增强环保意识，某中学举行了一次“环保知识竞赛”，共有900名学生参加了这次竞赛. 为了解本次竞赛成绩情况，从中抽取了部分学生的成绩(得分均为整数，满分为100分)进行统计. 请你根据尚未完成并有局部污损的频率分布表和频数分布直方图，解答下列问题：
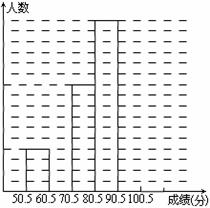
（1）填充频率分布表的空格(将答案直接填在表格内)；
（2）补全频数条形图；
（3）若成绩在75.5~85.5分的学生为二等奖，问获得二等奖的学生约为多少人？
18．（本小题满分14分）
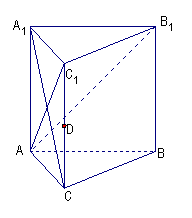如图所示，在侧棱垂直于底面的三棱柱
中，
，
，
，
．
（1）求四棱锥A－CBB1C1的体积；
（2）证明：
平面
；
（3）若是棱
的中点，在棱
上是否存在一点
，使
平面？证明你的结论．
19．（本小题满分12分）
2008年北京奥运会乒乓球比赛将产生男子单打、女子单打、男子团体、女子团体共四枚金牌，保守估计中国乒乓球男队获得每枚金牌的概率均为，中国乒乓球女队获得每枚金牌的概率均为
.
（1）求按此估计中国乒乓球女队比中国乒乓球男队多获得一枚金牌的概率；
（2）记中国乒乓球队获得金牌的数为
，按此估计的分布列和数学期望
。
20．(本题满分14分)
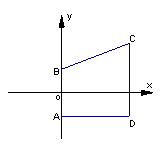
在梯形ABCD中，AB⊥AD,AB∥CD,A、B是两个定点，其坐
标分别为（0，－1）、（0，1），C、D是两个动点，且满足CD=BC.
(1)求动点C的轨迹E的方程；
(2)试探究在轨迹E上是否存在一点P？使得P到直线y＝x－2的
距离最短；
(3)设轨迹E与直线
所围成的图形的
面积为S,试求S的最大值。
其它解法请参照给分。
21．(本题满分14分)
数列
满足
．
（1）求数列{
}的通项公式；
（2）设数列{}的前项和为
，证明
．
参考答案及评分说明
一．选择题：ADDC ABAA
解析：1．
，其虚部为
，故选A.
3．
由已知可得
对应一切
上恒成立，易得
，故D.
4．由定义得
,选C.
5.∵
由知
，可排除B、C，由与的单调性相反可排除D,故选A.
6．设点A的坐标为
由，得
，解得
，
，故选B.
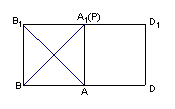
7．将面
绕棱
旋转到与
在同一平面内，如右图，由平几
知识知当点P与
重合时，取得最小值，最小值为2,故选A.
8．由
知，抛物线的对称轴为
，因抛物线开口向上，
如图易得答案选A.
二．填空题：
9．1；10．
；11．960；12．6 、
;13．
；14．
;15．
.
解析：9.单摆来回摆动一次所需的时间即函数的最小正周期，
10. 
，当且仅当
时，“＝”成立，
该几何体是由两个相同的圆锥组合而成，其表面积
11.将2位选手捆绑在一起，5名志愿者先排有
种排法，2位选手在5名志愿者排后的4个空档中任选一个插入，有
种插法，2位选手可交换位置，故共有
种。
12.依题意可知
，
，
，
，
，
,
,
13.由柯西不等式得
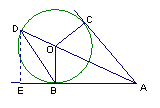14.过点D作DE⊥AE,由OB∥DE得
∴
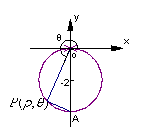15.在直角坐标系中，曲线是以点
为圆心，以１为半径的圆，如图
在
中，易得
，即曲线的极坐标方程为
。
三．解答题：
16.解：(1) ∵点的坐标为
，根据三角函数定义可知
， 
，
------2分
∴
-----------------------------------------------------------4分
(2)∵三角形
为正三角形，∴
，
，
-------5分
∴
--------------------------------------------------------------8分
∴
-----------------------------------------------------------------12分
17解：(1)
| 分组 | 频数 | 频率 |
| 50.5~60.5 | 4 | 0.08 |
| 60.5~70.5 | 8 | 0.16 |
| 70.5~80.5 | 10 | 0.20 |
| 80.5~90.5 | 16 | 0.32 |
| 90.5~100.5 | 12 | 0.24 |
| 合计 | 50 | 1.00 |
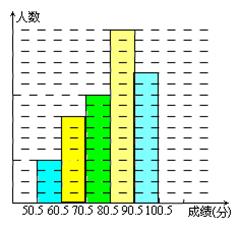
---------------------4分
(2) 频数直方图如右上所示--------------------------------8分
(3) 成绩在75.5~80.5分的学生占70.5~80.5分的学生的
，因为成绩在70.5~80.5分的学生频率为0.2 ，所以成绩在75.5~80.5分的学生频率为0.1 ，---------10分
成绩在80.5~85.5分的学生占80.5~90.5分的学生的
，因为成绩在80.5~90.5分的学生频率为0.32 ，所以成绩在80.5~85.5分的学生频率为0.16 -------------12分
所以成绩在75.5~85.5分的学生频率为0.26，
由于有900名学生参加了这次竞赛，
所以该校获得二等奖的学生约为0.26´900=234（人） ------------------14分
18.（1）解：∵三棱柱的侧棱垂直于底面，
∴
=
∴
-----------------------4分
(2) 证明：∵ 
∴ 
又∵
，∴
平面
．
∵
平面，∴
，在
中，∵，，∴
．
∵，∴四边形为正方形．
∴
．
∵
，∴平面．
-----------------------------8分
（3）解：当点为棱的中点时，平面．
--------------------10分
证明如下：
如图，取
的中点
，连
、
、
，
∵、、分别为、、的中点，
∴
．
∵
平面，
平面，
∴
平面
-----------------------12分
同理可证
平面．
∵
，
∴平面
平面．
∵
平面，
∴平面．
----------------------------------------------------------14分
19.解：（1）设中国乒乓球男队获0枚金牌，女队获1枚金牌为事件，中国乒乓球男队获1枚金牌，女队获2枚金牌为事件，那么，
=
=
--------4分
（2）根据题意中国乒乓球队获得金牌数是一随机变量，
它的所有可能取值为0，1，2，3，4（单位：枚）
那么
------------------------------------------5分
-----------------6分
------7分
----------------------8分
----------------------------------------------------------9分
则概率分布为：
|
| 0 | 1 | 2 | 3 | 4 |
|
|
|
|
|
|
|
那么，所获金牌的数学期望
（枚）
答：中国乒乓球队获得金牌数的期望为
枚.-------------------------------------------------12分
20(1) 解法1：依题意知，CD⊥AD,且CD=BC.
依抛物线的定义可知点C的轨迹是以B为焦点，以AD为准线的抛物线除去顶点和与直线y＝1的交点。 ---------------------------------------2分
∵OB=1 ∴C的轨迹E的方程为x2＝4y（x≠0，x≠
） -------------4分
解法2：设C(x，y)则CD=y+1,CB=
,
又CD=BC. 
，化简得：
x2＝4y（x≠0，x≠）
(2)解法1：设P（x，y）是轨迹E上一点，则P到直线y＝x－2的距离
当x＝2时，d取得最小值
，这时x＝2，y＝1， ---------------------7分
即点P(2,1).但由(Ⅰ)知点（2，1）不在轨迹E上，
∴在轨迹E上这样的点P不存在。 -------------------------------8分
解法2：所求点即与直线y＝x－2平行的轨迹E的切线与E的切点，
由
得
， 
，∴
，
下同解法1。
解法3：设与直线y＝x－2 平行，与抛物线E相切的直线为
x－y＋m＝0，由方程组
有一解得方程 
有两个相等的实根
∴ 
∴m＝－1从而得方程组的解为
，下同上.
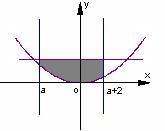
(3) ∵－2<a<0 ∴ 0<a+2<2
根据图形结合定积分的几何意义可得：
----------------------------11分
----------------------------13分
当
时，
------------- --------------14分
21.解：(1)方法一：∵
，
∴
．
---------------------------------------3分
∴
是首项为
，公差为
的等差数列． ---------------------------------4分
∴
，所以
．
----------------------------------------------------6分
方法二：
，
，
，猜测． ----------------------------------------2分
下用数学归纳法进行证明．
①当
时，由题目已知可知
，命题成立； -----------------------------------------3分
②假设当
(
)时成立，即
，那么
当
，
，
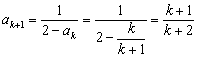也就是说，当时命题也成立． ----------------------------------------------------------------5分
综上所述，数列
的通项公式为． ----------------------------------------------------6分
（2） 设
则
--------------------------------------------------------------8分
∴函数
为
上的减函数，∴
，即
从而 
-----------------------------------------10分
----------------------------------------------------------11分
-----------------------13分
∴
--------------------------------------------------------------------------------14分