![]() 高三理科数学精编模拟题(理二)
高三理科数学精编模拟题(理二)
一.选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的![]()
1.特称命题“![]() 实数x,使
实数x,使![]() ”的否定可以写成
”的否定可以写成
A.若![]() B.
B.![]()
C.![]() D.
D.![]()
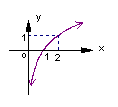 2.已知函数
2.已知函数![]() 是偶函数,
是偶函数,![]() 对应的图象如右图示,则
对应的图象如右图示,则![]() =
=
A.![]() B.
B.![]() C.
C. ![]() D.
D. ![]()
3. 对于任意的两个数对![]() 和
和![]() ,定义运算
,定义运算![]() ,若
,若![]() ,则复数
,则复数![]() 为
为
 A.
A.![]() B.
B. ![]() C.
C.![]() D.
D.![]()
4.设数列![]() 的通项公式为
的通项公式为![]() ,前
,前![]() 项和为
项和为![]() ,则
,则![]() 中最大的是
中最大的是
A.![]() B.
B.![]() 或
或![]() C.
C. ![]() D.
D. ![]()
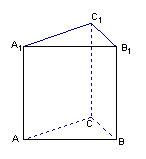
5.如图,三棱柱的侧棱长为2,底面是边长为2的正三角形,![]() ,
,
正视图是边长为2的正方形,则左视图的面积为B
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
6.已知点P(x,y)满足条件 y的最大值为8,则
y的最大值为8,则![]() 的值
的值
A.-6 B.6 C. 8 D.不确定
7.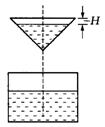 如图所示,液体从一圆锥形漏斗漏入一圆柱形桶中,开始时,漏斗盛满液体,经过3分钟漏完.已知圆柱中液面上升的速度是一个常量,H是圆锥形漏斗中液面下落的距离,则H与下落时间t(分)的函数关系表示的图象只可能是.
如图所示,液体从一圆锥形漏斗漏入一圆柱形桶中,开始时,漏斗盛满液体,经过3分钟漏完.已知圆柱中液面上升的速度是一个常量,H是圆锥形漏斗中液面下落的距离,则H与下落时间t(分)的函数关系表示的图象只可能是.
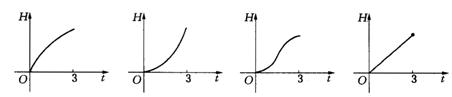
A B
A. B. C. D.
8.若关于![]() 的不等式
的不等式![]() 至少有一个负数解,则实数
至少有一个负数解,则实数![]() 的取值范围为是
的取值范围为是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题:本大题共6小题,每题5分,共30分.
必做题:第9、10、11、12题是必做题,每道试题考生都必须做答.
9.已知![]() ,若
,若![]()
![]() ,则
,则![]() .
.
| x | 2 | 3 | 4 | 5 |
| y | 1.2 | 2.5 | 3.5 | 4.8 |
10. 右表记录了某种汽车的使用年限x和所支出的费用y(万元)的统计资料,则用最小二乘法求出y关于x的线性回归方程为
;根据回归方程,估计使用年限为10年时,所支出的费用大约为
.(参考数据:![]() ,
,![]() )
)
11.按下列程序框图运算:

规定:程序运行到“判断结果是否大于244”为1次运算,若x=5,则运算进行 次才停止。
12.若点![]() 在
在![]()
![]() 内,则有结论
内,则有结论 ![]() ,把命题类比推广到空间,若点
,把命题类比推广到空间,若点![]() 在四面体
在四面体![]() 内,则有结论:_____________________________.
内,则有结论:_____________________________.
选做题:选做题:第13、14、15题是选做题,考生只能选做二题,三题全答的,只计算前二题的得分.
 13.直线
13.直线![]() (
(![]() 为参数)与圆
为参数)与圆![]() (
(![]() 为参数)相切,则此直线的倾
为参数)相切,则此直线的倾![]() .;
.;
14.不等式![]() 的解集是
.
的解集是
.
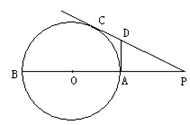
15.如图,已知![]() 、
、![]() 为⊙
为⊙![]() 的切线,
的切线,![]() 、
、![]() 分别为切点,
分别为切点,![]() 为⊙
为⊙![]()
的直径,若![]() ,
,![]() ,则
,则![]() .
.
三.解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
在△ABC中,角A、B、C的对边分别为a、b、c,若![]()
(1)判断△ABC的形状;
(2)若![]() 的值.
的值.
17. (本小题满分12分)
一医院从5名男医生和3名女医生中选出4人加入医疗队,赴四川地震灾区参加救援工作。设随机变量![]() 表示所选4人中女医生的人数。
表示所选4人中女医生的人数。
(1) 求![]() 的分布列;
的分布列;
 (2)
求
(2)
求![]() 的数学期望和方差。
的数学期望和方差。
18.(本小题满分14分)
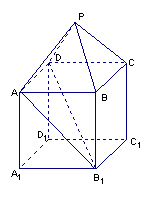
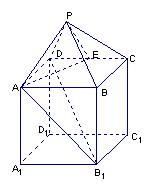
如图,在组合体中,![]() 是一个长方体,
是一个长方体,![]() 是一个
是一个
四棱锥.![]() ,
,![]() ,点
,点![]() 且
且![]() .
.
(1)证明:![]() ;
;
(2)求![]() 与平面
与平面![]() 所成的角的正切值;
所成的角的正切值;
(3)若![]() ,当
,当![]() 为何值时,
为何值时,![]() .
.
19.(本小题满分14分)
观察下列三角形数表
1 -----------第一行
2 2 -----------第二行
3 4 3 -----------第三行
4 7 7 4 -----------第四行
5 11 14 11 5
… … … …
… … … … …
假设第![]() 行的第二个数为
行的第二个数为![]() ,
,
(1)依次写出第六行的所有![]() 个数字;
个数字;
(2)归纳出![]() 的关系式并求出
的关系式并求出![]() 的通项公式;
的通项公式;
(3)设![]() 求证:
求证:![]() .
.
20. (本小题满分14分)
若存在实常数![]() 和
和![]() ,使得函数
,使得函数![]() 和
和![]() 对其定义域上的任意实数
对其定义域上的任意实数![]() 分别满足:
分别满足:![]() 和
和![]() ,则称直线
,则称直线![]() 为
为![]() 和
和![]() 的“隔离直线”.已知
的“隔离直线”.已知![]() ,
,![]() 为自然对数的底数).
为自然对数的底数).
(1)求![]() 的极值;
的极值;
(2)函数![]() 和
和![]() 是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.
21.(本小题满分14分)
 已知点H(-3,0),点P在
已知点H(-3,0),点P在![]() 轴上,点Q在
轴上,点Q在![]() 轴的正半轴上,点M在直线PQ上,且满足
轴的正半轴上,点M在直线PQ上,且满足![]() ,
,
![]()
![]() .
.
(1)当点P在![]() 轴上移动时,求点M的轨迹C;
轴上移动时,求点M的轨迹C;
(2)过定点![]() 作直线
作直线![]() 交轨迹C于A、B两点,E
交轨迹C于A、B两点,E
是D点关于坐标原点O的对称点,求证:![]() ;
;
(3)在(2)中,是否存在垂直于![]() 轴的直线
轴的直线![]() 被以AD为直径
被以AD为直径
的圆截得的弦长恒为定值?若存在求出![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
参考答案及评分说明
一.选择题:DCDB BABA
2.由图象可得![]() (
(![]() )因函数的图象关于y轴对称,可得
)因函数的图象关于y轴对称,可得![]() (
(![]() ),选C
),选C
3.由![]() 得
得![]() ,选D.
,选D.
4. 由![]() ≥0得
≥0得![]() ≤5,所以
≤5,所以![]() 或
或![]() 最大,选B.
最大,选B.
5.左视图是长为2,宽为![]() 的长方形,故面积为
的长方形,故面积为![]() ,选B
,选B
6.画图,联立方程![]() 得
得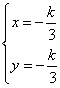 ,代入
,代入![]() ,选A.
,选A.
 8.解法1:取
8.解法1:取![]() ,得不等式
,得不等式![]() 有负数解
有负数解![]() ,排除选项B、C,取
,排除选项B、C,取![]() ,不等式
,不等式![]() 无负数解,排除D,故选A
无负数解,排除D,故选A
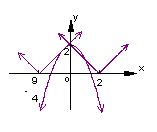
解法2:将原不等式变形为![]() ,在同一坐标系内作出函数
,在同一坐标系内作出函数
![]() 和
和![]() 的图象,函数
的图象,函数![]() 的图象是从点
的图象是从点![]() 出
出
发的两条射线,如图,当射线![]() 过点
过点![]() 时,
时,![]() ,当射线
,当射线
![]() 与抛物线
与抛物线![]() 相切时,
相切时,![]() ,结合图象易得
,结合图象易得![]()
二.填空题:9.5;10.
![]() 、10.67万元;11.4;
、10.67万元;11.4;
12. ![]() ;13.
;13.![]() 或
或![]() ;14.
;14. ![]() ;
;
15. ![]() .
.
解析:
11.第一次运算得13,第二次运算得37,第三次运算得109,第四次运算得325.
三.解答题:
16.解:(1)![]() ------------------------------------1分
------------------------------------1分
![]() 得
得![]() ,即
,即![]()
由正弦定理得
![]() --------------------------------------------------------------------3分
--------------------------------------------------------------------3分
即![]()
![]() -------------------------------------------------------------------------------5分
-------------------------------------------------------------------------------5分
![]()
![]() 为等腰三角形. ---------------7分
为等腰三角形. ---------------7分
(2)由(1)知![]()
![]() --------------10分
--------------10分
![]()
![]() --------------------------------12分
--------------------------------12分
17.解:(1)能取的值为![]() ,3.
,3.
![]() --------------------------- ----3分
--------------------------- ----3分
∴![]() 的分布列为
的分布列为
|
| 0 | 1 | 2 | 3 |
| P |
|
|
|
|
-----------------6分
(2)由(1)知![]() 的数学期望为
的数学期望为
![]()
![]() ---------------------------9分
---------------------------9分
方差![]() --------------------12分18(1)证明:∵
--------------------12分18(1)证明:∵![]() ,
,![]() ,∴
,∴![]() 为等腰直角三角形,∴
为等腰直角三角形,∴![]() . ……1分
. ……1分
∵![]() 是一个长方体,∴
是一个长方体,∴![]() ,而
,而![]() ,
,
∴![]() ,所以
,所以![]() .
……3分
.
……3分
 ∵
∵![]() 垂直于平面
垂直于平面![]() 内的两条相交直线
内的两条相交直线![]() 和
和![]() ,由线面垂直的判定定理,可得
,由线面垂直的判定定理,可得![]() .…4分
.…4分
(2)解:过![]() 点在平面
点在平面![]() 作
作![]() 于
于![]() ,连接
,连接![]() .……5分
.……5分
∵![]() ,∴
,∴![]() ,
,
∴![]() 就是
就是![]() 与平面
与平面![]() 所成的角.……6分
所成的角.……6分
∵![]() ,
,![]() ,∴
,∴![]() .……7分
.……7分
∴![]() 与平面
与平面![]() 所成的角的正切值为
所成的角的正切值为![]() . ……8分
. ……8分
(3)解:当![]() 时,
时,![]() .
……9分
.
……9分
 当
当![]() 时,四边形
时,四边形![]() 是一个正方形,所以
是一个正方形,所以![]() ,而
,而![]() ,所以
,所以![]() ,∴
,∴![]() .
……10分
.
……10分
而![]() ,
,![]() 与
与![]() 在同一个平面内,所以
在同一个平面内,所以![]() .……12分
.……12分
而![]() ,∴
,∴![]() ,
,
∴![]() . ……14分
. ……14分
方法二:(1)建立空间直角坐标系,设棱长![]() ,则有
,则有![]() ,
,![]() ,
,![]() ,
,![]() .
--------------------------------------------------------1分
.
--------------------------------------------------------1分
于是![]() ,
,![]() ,
,![]() ,∴
,∴![]() ,
,![]() .……3分
.……3分
∴![]() 垂直于平面
垂直于平面![]() 内的两条相交直线
内的两条相交直线![]() 和
和![]() ,由线面垂直的判定定理,可得
,由线面垂直的判定定理,可得![]() .
……4分
.
……4分
(2![]() ,∴
,∴![]() ,而平面
,而平面![]() 的一个法向量为
的一个法向量为![]() .…5分
.…5分
∴![]() .
……6分
.
……6分
∴![]() 与平面
与平面![]() 所成的角的正弦值为
所成的角的正弦值为![]() .
……7分
.
……7分
∴![]() 与平面
与平面![]() 所成的角的正切值为
所成的角的正切值为![]() .
……8分
.
……8分
(3![]() ,∴
,∴![]() ,
,![]() .设平面
.设平面![]() 的法向量为
的法向量为![]() ,则有
,则有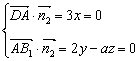 ,令
,令![]() ,可得平面
,可得平面![]() 的一个法向量为
的一个法向量为![]() ……10分
……10分
若要使得![]() ,则要
,则要![]() ,即
,即![]() ,解得
,解得![]() .…12分
.…12分
∴当![]() 时,
时,![]() . ……14分
. ……14分
19.解:(1)第六行的所有6个数字分别是6,16,25,25,16,6; --------------2分
(2)依题意![]() ,
,![]() -------------------------------5分
-------------------------------5分
![]() ------------------------7分
------------------------7分
![]()
∴![]() ; -------------------------------------9分
; -------------------------------------9分
(3)∵![]() ∴
∴![]() -------------11分
-------------11分
∴![]()
![]()
![]() ---14分
---14分
20.解(1) ![]()
![]() ,
,
![]() .
…………………………2分
.
…………………………2分
当![]() 时,
时,![]() .
…………………………3分
.
…………………………3分
![]() 当
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 递减;
递减;
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 递增;
递增;
∴当![]() 时,
时,![]() 取极小值,其极小值为
取极小值,其极小值为![]() .
…………………………6分
.
…………………………6分
(2)解法一:由(1)可知函数![]() 和
和![]() 的图象在
的图象在![]() 处有公共点,因此若存在
处有公共点,因此若存在![]() 和
和![]() 的隔离直线,则该直线过这个公共点.
…………………………7分
的隔离直线,则该直线过这个公共点.
…………………………7分
设隔离直线的斜率为![]() ,则直线方程为
,则直线方程为![]() ,即
,即
![]() .
…………………………8分
.
…………………………8分
由![]() ,可得
,可得![]() 当
当![]() 时恒成立.
时恒成立.
![]() ,
,
![]() 由
由![]() ,得
,得![]() .
…………………………10分
.
…………………………10分
下面证明![]() 当
当![]() 时恒成立.
时恒成立.
令![]()
![]() ,则
,则
![]() ,
…………………………11分
,
…………………………11分
当![]() 时,
时,![]() .
.
![]() 当
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 递增;
递增;
当![]() 时,
时,![]() ,此时函数
,此时函数![]() 递减;
递减;
∴当![]() 时,
时,![]() 取极大值,其极大值为
取极大值,其极大值为![]() .
.
从而![]() ,即
,即![]() 恒成立.………13分
恒成立.………13分
∴函数![]() 和
和![]() 存在唯一的隔离直线
存在唯一的隔离直线![]() . ………………………14分
. ………………………14分
解法二: 由(Ⅰ)可知当![]() 时,
时,![]() (当且当
(当且当![]() 时取等号) .……7分
时取等号) .……7分
若存在![]() 和
和![]() 的隔离直线,则存在实常数
的隔离直线,则存在实常数![]() 和
和![]() ,使得
,使得
![]() 和
和![]() 恒成立,
恒成立,
令![]() ,则
,则![]() 且
且![]()
![]() ,即
,即![]() .
…………………………8分
.
…………………………8分
后面解题步骤同解法一.
21.解:(1)设![]() ,
,
![]()
![]()
![]() 且
且![]() , -------------------2分
, -------------------2分
![]() -------------------------------------------------3分
-------------------------------------------------3分
![]() .
--------------------------------------------------------------------------4分
.
--------------------------------------------------------------------------4分
∴动点M的轨迹C是以O(0,0)为顶点,以(1,0)为焦点的抛物线(除去原点)------5分
(2)解法一:①当直线![]() 垂直于
垂直于![]() 轴时,根据抛物线的对称性,有
轴时,根据抛物线的对称性,有![]() ;
;
-------------------------6分
②当直线![]() 与
与![]() 轴不垂直时,依题意,可设直线
轴不垂直时,依题意,可设直线![]() 的方程为
的方程为![]() ,
,![]() ,则A,B两点的坐标满足方程组
,则A,B两点的坐标满足方程组
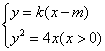
消去![]() 并整理,得
并整理,得
![]() ,
,
![]() .
---------------7分
.
---------------7分
设直线AE和BE的斜率分别为![]() ,则:
,则:
![]() =
=![]()
![]()
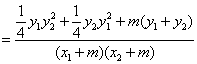
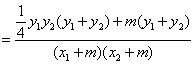
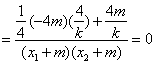 . -------------------9分
. -------------------9分
![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() .
.
综合①、②可知![]() .
--------------------------10分
.
--------------------------10分
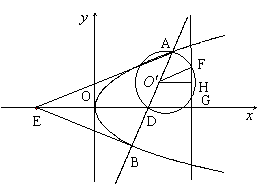 解法二:依题意,设直线
解法二:依题意,设直线![]() 的方程为
的方程为![]() ,
,![]() ,则A,B两点的坐标满足方程组:
,则A,B两点的坐标满足方程组:
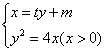
消去![]() 并整理,得
并整理,得
![]() ,
,
![]() . -------------------------7分
. -------------------------7分
设直线AE和BE的斜率分别为![]() ,则:
,则:
![]() =
=![]()
![]()
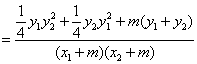
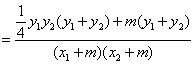
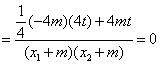 .
-------------------9分
.
-------------------9分
![]() ,
,
![]() ,
,
![]() ,
,![]()
![]() .
-------------------------------------10分
.
-------------------------------------10分
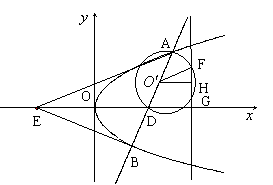
(3)假设存在满足条件的直线![]() ,其方程为
,其方程为![]() ,AD的中点为
,AD的中点为![]() ,
,![]() 与AD为直径的圆相交于点F、G,FG的中点为H,则
与AD为直径的圆相交于点F、G,FG的中点为H,则![]() ,
,![]() 点的坐标为
点的坐标为![]() .
.
![]()
![]() ,
,
![]() ,
,
![]()
![]()
![]() .
----------------------------------------12分
.
----------------------------------------12分
![]() ,
,
令![]() ,得
,得![]()
此时,![]() .
.
∴当![]() ,即
,即![]() 时,
时,![]() (定值).
(定值).
∴当![]() 时,满足条件的直线
时,满足条件的直线![]() 存在,其方程为
存在,其方程为![]() ;当
;当![]() 时,满足条件的直线
时,满足条件的直线![]() 不存在.-----------------------------14分
不存在.-----------------------------14分