高三理科数学起点考试试卷
一、选择题(本大题共10小题,每小题5分,共50分. 在每小题给出的四个选项中,只有一项是符合题目要求的.)
1.已知![]() 为等差数列
为等差数列![]() 中的第8项,则二项式
中的第8项,则二项式![]() 展开式中常数项是( )
展开式中常数项是( )
A. 第7项 B.第8项 C.第9项 D.第10项
2.设![]() ,
,![]() ,
,![]() ,则
,则![]() 与
与![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.下列电路图中,闭合开关A是灯泡B亮的必要不充分条件的是 ( )
|
4.下列函数在x=0处连续的是 ( )
A.f(x)=![]() B.f(x) =lnx
B.f(x) =lnx
C.f(x)=![]() D.f(x)=
D.f(x)=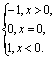
5.已知函数![]() 的最小值为
的最小值为
( )
A.1 B.![]() C.
C.![]() D.
D.![]()
6.![]() 的三内角A,B,C所对边长分别是
的三内角A,B,C所对边长分别是![]() ,设向量
,设向量![]()
![]() ,若
,若![]() ,则角
,则角![]() 的大小为 ( )
的大小为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
7.如果以原点为圆心的圆经过双曲线![]() 的焦点,而被该双曲线的右准线分成弧长为2:1的两段圆弧,则该双曲线的离心率等于 ( )
的焦点,而被该双曲线的右准线分成弧长为2:1的两段圆弧,则该双曲线的离心率等于 ( )
A.![]() B.
B.
![]() C.
C.![]() D.
D.
![]()
8.有两个同心圆,在外圆周上有相异6个点,内圆周上有相异3个点,由这9个点决定的直线至少有 ( )
A.36条 B.30条 C.21条 D.18条
9.记满足下列条件的函数f(x)的集合为M:当x1≤1,x2≤1时, f(x1)-f(x2)≤4x1-x2.若有函数g(x)=x2+2x-1, 则g(x)与M的关系是( )
A.g(x)![]() M B.g(x)
M B.g(x)![]() M C.g(x)
M C.g(x)![]() M D.不能确定
M D.不能确定
|
A.2个 B.5个 C.6个 D.无数个
二、填空题(本大题共5小题,每小题5分,共25分,把答案填在答题卡相应的位置上)
11.已知某人投篮的命中率为![]() ,则此人投篮4次,至少命中3次的概率是
。
,则此人投篮4次,至少命中3次的概率是
。
12.已知随机变量![]() ,若ξ=2η+3,则Dη=____________.
,若ξ=2η+3,则Dη=____________.
| |
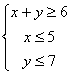 ,则
,则14.设![]() = .
= .
15. 行驶中的汽车在刹车时由于惯性作用,要继续往前滑行一段距离才能停下,这段距离叫做刹车距离。在某种路面上,某种型号汽车的刹车距离y(米)与汽车的车速x(千米/时)满足下列关系:![]() (m,n是常数),如图是根据多次实验数据绘制的刹车距离y(米)与汽车的车速x(千米/时)的关系图.
(m,n是常数),如图是根据多次实验数据绘制的刹车距离y(米)与汽车的车速x(千米/时)的关系图.
(I)y关于x的函数表达式为:___________
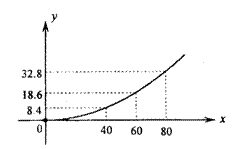 (II)如果要求刹车距离不超过25.2米,则行驶的最大速度为:__________
(II)如果要求刹车距离不超过25.2米,则行驶的最大速度为:__________
三、解答题(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤)
16.(本小题满分12分)
已知函数![]()
(I)若函数![]() 的图象关于直线
的图象关于直线![]() 对称,求a的最小值;
对称,求a的最小值;
(II)若存在![]() 成立,求实数m的取值范围.
成立,求实数m的取值范围.
17.(本小题满分12分)
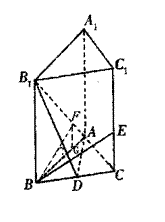
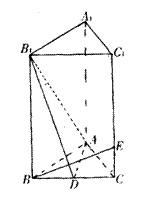 如图在直三棱柱ABC – A1B1C1中,∠BAC = 90°,AB = AC = a,AA1 = 2a,D为BC的中点,E为CC1上的点,且CE =
如图在直三棱柱ABC – A1B1C1中,∠BAC = 90°,AB = AC = a,AA1 = 2a,D为BC的中点,E为CC1上的点,且CE = ![]() CC1
CC1
(I)求三棱锥B – AB1D的体积;
(II)求证:BE⊥平面ADB1;
(Ⅲ)求二面角B—AB1—D的大小.
18.(本小题满分12分)
口袋里装有大小相同的4个红球和8个白球,甲、乙两人依规则从袋中有放回摸球,每次摸出一个球,规则如下:若一方摸出一个红球,则此人继续下一次摸球;若一方摸出一个白球,则由对方接替下一次摸球,且每次摸球彼此相互独立,并由甲进行第一次摸球。求在前三次摸球中,甲摸得红球的次数ξ的分布列及数学期望;
19.(本小题满分12分)
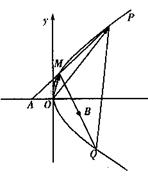
已知点A(-1,0),B(1,-1)和抛物线.![]() ,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
,O为坐标原点,过点A的动直线l交抛物线C于M、P,直线MB交抛物线C于另一点Q,如图.
(I)若△POM的面积为![]() ,求向量
,求向量![]() 与
与![]() 的夹角。
的夹角。
(II)试证明直线PQ恒过一个定点。
20.(本小题满分13分)
设函数![]()
(I)k为何值时,f(x)在R上是减函数;
(II)试确定实数k的值,使![]() 的极小值为0.
的极小值为0.
21.(本小题满分14分)
已知函数![]()
(1)求![]() 的值;
的值;
(2)数列{an}满足![]() 数列{an}
数列{an}
是等差数列吗?请给予证明;
(3)![]() ,试比较Tn与Sn的大小.
,试比较Tn与Sn的大小.
数学答案(理科)
一、选择题:
CABAC BDCBB
二、填空题:
11.![]() 12.1
12.1
| |
15.(I)![]() (II)70千米/时
(II)70千米/时
三、解答题
16.解:(I)![]() …………………………(4分)
…………………………(4分)
由题设,![]()
![]() ………………………………………………(6分)
………………………………………………(6分)
(II)当![]()
![]() …………………………………………………………………(9分)
…………………………………………………………………(9分)
由![]()
故m的取值范围是![]() …………………………………………(12分)
…………………………………………(12分)
17.解:(Ⅰ)∵AB=AC=a,∠BAC=90°,D为BC中点
B1B=C1C=A1A=2a,![]()
∴![]() ………………2分
………………2分
∵![]() …………4分
…………4分
解法一:
(Ⅱ)由AB=AC,D是BC的中点,得AD⊥BC
从而AD⊥平面B1BCC1
又BE![]() 平面B1BCC1,所在AD⊥BE …………6分
平面B1BCC1,所在AD⊥BE …………6分
 由已知∠BAC=90°,AB=AC=a,得
由已知∠BAC=90°,AB=AC=a,得![]()
在Rt△BB1D中,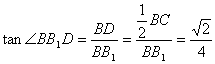
在Rt△CBE中,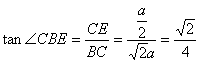
于是∠BB1D=∠CBE,设EB∩DB1=G
∠BB1D+∠B1BG=∠CBE+∠B1BG=90°,则DB1⊥BE,又AD∩DB1=D
故BE⊥平面ADB1 ……………………8分
(Ⅲ)过点G作GF⊥AB1于F,连接BF
由(Ⅰ)及三垂线定理可知∠BFG是二面角B—AB1—D的平面角 …………10分
在Rt△ABB1中,由BF·AB1=BB1·AB,得![]()
在Rt△BDB1中,由BB1·BD=BG·DB1,得BG=![]()
所以在Rt△BFG中,![]()
故二面角B—AB—D的大小为arcsin![]() ………………12分
………………12分
解法二:
解法:(Ⅱ)如图,建立空间直角坐标系A-xyz …………2分
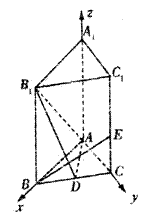 可知A(0,0,0),B(a,0,0),C(0,a,0),D(
可知A(0,0,0),B(a,0,0),C(0,a,0),D(![]() ),
),
B1(a,0,2a),E(0,a,![]() ) …………4分
) …………4分
可得 ![]()
![]() ………………6分
………………6分
于是得![]() ,可知BE⊥AD,BE⊥DB1
,可知BE⊥AD,BE⊥DB1
又AD∩DB1=D,故BE⊥平面ADB1 …………8分
(Ⅲ)由(Ⅱ)知平面ADB1的法向量![]() ,平面ABB1的法向量
,平面ABB1的法向量![]()
于是 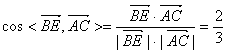 …………10分
…………10分
故二面角B—AB1—D的大小为arccos![]() ………………12分
………………12分
18.解:记“甲摸球一次摸出红球”为事件A,“乙摸球一次摸出红球”为事件B,则
![]() ,且A、B相互独立.………………(2分)
,且A、B相互独立.………………(2分)
据题意,ξ的可能取值为0,1,2,3,其中
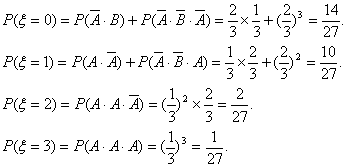 ………………(8分)
………………(8分)
| ξ | 0 | 1 | 2 | 3 |
| p | 14/27 | 10/27 | 2/27 | 1/27 |
………………(10分)
![]()
19.解:(I)设点![]() 、M、A三点共线,
、M、A三点共线,
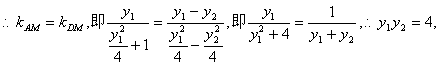 ……(2分)
……(2分)
![]() ……………………………………………(4分)
……………………………………………(4分)
设∠POM=α,则![]()
![]() 由此可得tanα=1.…………………(6分)
由此可得tanα=1.…………………(6分)
又![]() ……………………(7分)
……………………(7分)
(II)设点![]() 、B、Q三点共线,
、B、Q三点共线,![]()
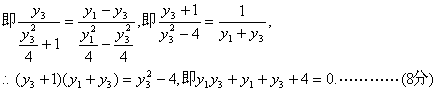
![]()
即![]() ……………………………………(9分)
……………………………………(9分)

即![]() ……………………(10分)
……………………(10分)
由(*)式,![]() 代入上式,得
代入上式,得![]()
由此可知直线PQ过定点E(1,-4).…………………………………………(12分)
20.解:(Ⅰ)∵![]()
∴![]()
![]() ………………2分
………………2分
当k=4时,![]()
∴当k=4时,![]() 上是减函数………………5分
上是减函数………………5分
(Ⅱ)当k≠4时,令![]() ………………6分
………………6分
当k<4时,即![]() 有
有
| x |
|
| ( | 2 | (2,+∞) |
|
| - | 0 | + | 0 | - |
|
| ↘ | 极小 | ↗ | 极大 | ↘ |
令![]() ∴k=0 ………………9分
∴k=0 ………………9分
②当k>4时,即![]() >2有
>2有
| x |
| 2 | (2, |
| ( |
|
| - | 0 | + | 0 | - |
|
| ↘ | 极小 | ↗ | 极大 | ↘ |
令![]() ∴k=8………………12分
∴k=8………………12分
∴当k=0或k=8时,![]() 有极小值0 ………………13分
有极小值0 ………………13分
21.(1)解:f(x)对任意![]()
![]() ………………2分
………………2分
令![]()
![]() ……………………………………4分
……………………………………4分
(2)解:数列{an}是等差数列
f(x)对任意x∈R都有![]()
则令![]() ……………………………………6分
……………………………………6分
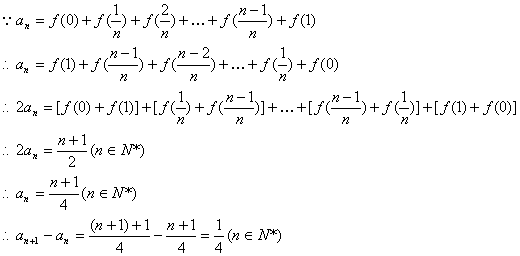 ∴{an}是等差数列. ………………10分
∴{an}是等差数列. ………………10分
(3)解:由(2)有![]()
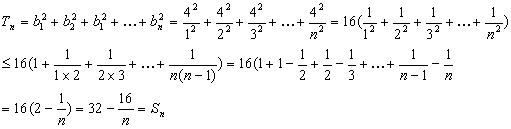
∴Tn≤Sn…………………………………………………………………………14分
该题也可用数学归纳法做。
