高三级数学选修导数与复数测试题
时间:120分钟 满分:150分 姓名
一、选择题:本大题共12小题,每小题5分,共60分
1.函数y = (1-sinx)![]() 的导数是( )
的导数是( )
A.y=2sin2x-cosx B. y=sin2x+2cosx C.y=2sin2x-2cosx D .y=sin2x-2cosx
2.设![]() ,则
,则![]() 等于( )
等于( )
A .-1
B.
3.复数![]() 等于( )
等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.函数![]() =
=![]()
![]() ,则
,则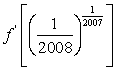 =( )
=( )
A . 0
B .
5.(2008重庆卷4)已知函数y=![]() 的最大值为M,最小值为m,则
的最大值为M,最小值为m,则![]() 的值为 ( )
的值为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.曲线![]() 在点(1 ,
在点(1 ,![]() )处切线的倾斜角为( )
)处切线的倾斜角为( )
A.![]() B.
B.![]() C.
C. ![]() D.
D.![]()
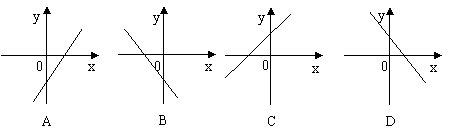
7.![]() 的图象开口向上,且顶点在第二象限,则
的图象开口向上,且顶点在第二象限,则![]() 的图象大概是( )
的图象大概是( )
 |
8.设![]() 是定义在R上的偶函数,当
是定义在R上的偶函数,当![]() 时,
时,![]() ,且
,且![]() ,则不等式
,则不等式![]() 的解集为( )
的解集为( )
A.(-1,0)∪(1,+![]() ) B.(-1,0)∪(0,1)
) B.(-1,0)∪(0,1)
C.(-![]() ,-1)∪(1,+
,-1)∪(1,+![]() ) D.(-
) D.(-![]() ,-1)∪(0,1)
,-1)∪(0,1)
9.对于R上可导的任意函数f(x),若满足(x-1)![]() ³0,则必有( )
³0,则必有( )
A.f(0)+f(2)<
C. f(0)+f(2)³
10.函数![]() 的单调减区间是( )
的单调减区间是( )
A.![]() B.
B.![]() C.
C.![]() 及
及![]() D.
D.![]()
11.已知![]()
![]()
![]() ( )
( )
A.1+2i B.1-2i C.2+i D.2
12.已知f'(0)=2,则![]()
![]() =( )
=( )
A.4
B.-
二、填空题:本大题共4小题;每小题4分,共16分
13.已知函数![]() 在R上可导,函数
在R上可导,函数![]() ,则
,则![]()
14.f(x)= 1+3sin x + 4cos x取得最大值时tan x =
15.设![]() 、
、![]() 为实数,且
为实数,且![]() ,则
,则![]() +
+![]() =_________
=_________
16.(2008江苏卷14)![]() 对于
对于![]() 总有
总有![]() ≥0 成立,则
≥0 成立,则![]() =
=
三、解答题:本大题共6小题,共74分
17.(12)已知![]() ,求
,求![]() 的值。
的值。
18.(12)(20008全国Ⅰ卷19)已知函数![]() ,
,![]() .
.
(Ⅰ)讨论函数![]() 的单调区间;
的单调区间;
(Ⅱ)设函数![]() 在区间
在区间![]() 内是减函数,求
内是减函数,求![]() 的取值范围.
的取值范围.
19.(12)已知函数![]() ,(a
,(a![]() R),设曲线
R),设曲线![]() 在点(1
在点(1 ![]() )处的切线为
)处的切线为![]() ,若
,若![]() 与圆C:
与圆C: ![]() 相切,求a的值
相切,求a的值
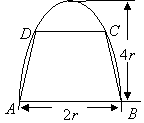 20.(12)有一块半椭圆形钢板,其半轴长为
20.(12)有一块半椭圆形钢板,其半轴长为![]() ,短半轴长为
,短半轴长为![]() ,计划将此钢板切割成等腰梯形的形状,下底
,计划将此钢板切割成等腰梯形的形状,下底![]() 是半椭圆的短轴,上底
是半椭圆的短轴,上底![]() 的端点在椭圆上,记
的端点在椭圆上,记![]() ,梯形面积为
,梯形面积为![]() .
.
(I)求面积![]() 以
以![]() 为自变量的函数式,并写出其定义域;
为自变量的函数式,并写出其定义域;
(II)求面积![]() 的最大值.
的最大值.
21.(12)已知函数![]()
(1)求函数f (x)的单调区间; (2)求证:x > 1时,![]()
22.(2008天津卷21)(14分)已知函数![]() (
(![]() ),其中
),其中![]() .
.
(Ⅰ)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 仅在
仅在![]() 处有极值,求
处有极值,求![]() 的取值范围;
的取值范围;
(Ⅲ)若对于任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
(导数与复数)参考答案
一 DBABC DCACA CD
二 13. 0
14. ![]() 15. 4 16. 4
15. 4 16. 4
三.17.解:![]() =
=![]()
![]()
18.解:解:(1)![]() 求导:
求导:![]()
当![]() 时,
时,![]() ,
,![]() ,
,![]() 在
在![]() 上递增
上递增
当![]() ,
,![]() 求得两根为
求得两根为![]()
即![]() 在
在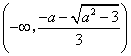 递增,
递增,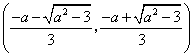 递减,
递减,
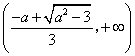 递增
递增
(2)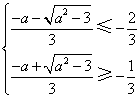 ,且
,且![]() 解得:
解得:![]()
19.解:依题意有:![]() = a,
= a, ![]() =2ax+
=2ax+![]() (x<2)
(x<2)
![]() 方程为
方程为![]() =0
=0
![]() 与圆相切
与圆相切 ![]()
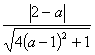 =
=![]()
![]() a=
a=![]()
20.解:(I)依题意,以![]() 的中点
的中点![]() 为原点建立直角坐标系
为原点建立直角坐标系![]() (如图),则点
(如图),则点![]() 的横坐标为
的横坐标为![]() .
.
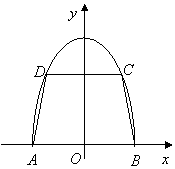 点
点![]() 的纵坐标
的纵坐标![]() 满足方程
满足方程![]() ,
,
解得![]()
![]()
![]() ,
,
其定义域为![]() .
.
(II)记![]() ,
,
则![]() .
.
令![]() ,得
,得![]() .
.
因为当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ,所以
,所以![]() 是
是![]() 的最大值.
的最大值.
因此,当![]() 时,
时,![]() 也取得最大值,最大值为
也取得最大值,最大值为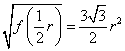 .
.
即梯形面积![]() 的最大值为
的最大值为![]() .
.
21.解 1)依题意知函数的定义域为x > 0. ![]() ,
,
所以,当a≤0时,f (x)的单调递增区间为(0,+∞)
当![]() 时,
时,![]() ,令
,令![]() ,有
,有![]() ;
;
所以函数f (x)的单调递增区间为![]() ;令
;令![]() ,有
,有![]()
所以函数f (x)的单调递减区间为![]() .
.
(2)设![]()
![]() 时,
时,![]() ,
,
所以g (x)在(1,+∞)上是增函数,
![]()
∴当x>1时,![]()
22.(Ⅰ)解:![]() .
.
当![]() 时,
时,![]() .
.
令![]() ,解得
,解得![]() ,
,![]() ,
,![]() .
.
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
| 0 |
|
|
| 2 |
|
|
| - | 0 | + | 0 | - | 0 | + |
|
| ↘ | 极小值 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以![]() 在
在![]() ,
,![]() 内是增函数,在
内是增函数,在![]() ,
,![]() 内是减函数.
内是减函数.
(Ⅱ)解:![]() ,显然
,显然![]() 不是方程
不是方程![]() 的根.
的根.
为使![]() 仅在
仅在![]() 处有极值,必须
处有极值,必须![]() 成立,即有
成立,即有![]() .
.
解些不等式,得![]() .这时,
.这时,![]() 是唯一极值.
是唯一极值.
因此满足条件的![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)解:由条件![]() ,可知
,可知![]() ,从而
,从而![]() 恒成立.
恒成立.
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
因此函数![]() 在
在![]() 上的最大值是
上的最大值是![]() 与
与![]() 两者中的较大者.
两者中的较大者.
为使对任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,当且仅当
上恒成立,当且仅当![]() ,即
,即![]() ,在
,在![]() 上恒成立.
上恒成立.
所以![]() ,因此满足条件的
,因此满足条件的![]() 的取值范围是
的取值范围是![]() .
.
由(1)知a n> a ![]() (
(![]() )
)
故 对任意正整数n都有a n> a n+1。