高三级数学（文科）上学期周练一
（注：8月2日交）
班级： 姓名：
1．已知集合
，则
（ ）
A．
B．
C．
D．
2.若集合
则B的子集的个数为（ ）
A．2 B．4 C．6 D．8
3．集合
=（ ）
A．
B．{1} C．{0,1,2}
D． {－1,0,1,2}
4. 复数
的虚部为（ ）
. －2 
.2 
. 
. 
5．
设集合
，
，那么“
”是“
”的（ ）
A．充分而不必要条件 B．必要而不充分条件
C．充分必要条件 D．既不充分也不必要条件
6．已知集合
，集合
.若
,则实数m=( )
A．－2 B．2 C．－1 D．1
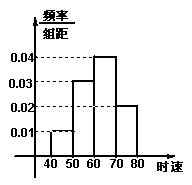7. 等差数列
中，
是前
项的和，若
，则
（ ）
A 15 B 18 C 9 D 12
8. 
辆汽车通过某一段公路时的时速的频率分布直方图
如右图所示，时速在
的汽车大约有 （
）
.
辆 . 
辆 .
辆 .80辆
9．已知不等式
，则
的解集为（ ） 
10． 函数
的单调递增区间是
A．
B．
C．
D．
11.不等式
＜1解集为_______
12.若不等式
＞0的解集为{x-3＜x＜ -1或x＞2＝,则
=____________
13. 规定记号“
”表示一种运算，即
，若
对任意实数
都成立，则实数
的取值范围是 ___.
选做题：在下面两道小题中选做一题，两题都选只计算前一题的得分.
14.在直角坐标系
中，已知曲线的参数方程是
（
是参数），若以
为极点，
轴的正半轴为极轴，则曲线的极坐标方程可写为________________.
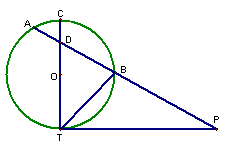15. 已知：如图，PT切⊙O于点T，PA交⊙O于A、B两点且与直径CT交于点D，CD＝2，AD＝3， BD＝6，则PB＝ ．
16．设全集
，集合
，集合
(Ⅰ)求集合与；
(Ⅱ)求
、
17. 已知函数
.
（I）求函数
的最小正周期;
(II)当
时,求函数的最大值,最小值.
18．在
中,
.
(Ⅰ)求
;
(Ⅱ) 记
的中点为,求中线
的长.
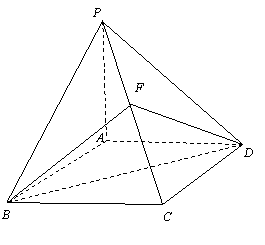19. 如图，已知四棱锥
的底面
是菱形,
平面, 点
为
的中点.
（Ⅰ）求证:
平面
;
（Ⅱ）求证:
平面
.
20.数列{an}中，a1＝8，
，且满足：
（n∈N*），
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设
，是否存在最大的整数m，使得任意的n均有
总成立？若存在，求出m若不存在，请说明理由．
广东北江中学高三级数学（文科）周练一答案
ABCAB DDCDB
11．{xx＜0或x＞-3 12.-2 
14. 
, 15. 15
16．解：(Ⅰ)
，不等式的解为
，
，
(Ⅱ)由(Ⅰ)可知
，
，
，
17. （I）
.
3分
的最小正周期为
.
5分
(Ⅱ).
,
7分
10分
.
当时,函数的最大值为1,最小值为
.
12分
18．解: (Ⅰ)由
, 是三角形内角，得
………..2分
∴ 
………………………………………..5分
…………………………………………………………6分
(Ⅱ) 在
中,由正弦定理，
，
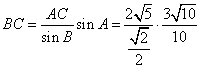
…………………………………………………………………………………………………..9分
, ,
由余弦定理得:
=
…………………………………12分
19.（Ⅰ）证明: 连结
，
与交于点
，连结
.…… 1分
是菱形, 
是的中点.
点为的中点, 
. …… 4分
平面
平面,
平面. 7分
(Ⅱ)证明: 平面,
平面,
.
…… 10分
是菱形, 
.
…… 12分
， 
平面. …… 14分
20. 解：（Ⅰ）∵an+2－2an+1＋an＝0，∴an+2－an+1＝an+1－an（n∈N*），∴{an}是等差数列，设公差为d，
∵a1＝8，a4＝a1＋3d＝8＋3d＝2，∴d＝－2， ∴an＝8＋（n－1）·（－2）＝10－2n．
（Ⅱ）
假设存在整数m满足总成立，
又
∴数列{
}是单调递增的，∴
为的最小值，故
，即m＜8，又m∈N*，
∴适当条件的m的最大值为7．