高三（文科）数学双周练试卷

高三（文科）数学双周练试卷

2008-7-26

一、填空题：(每小题5分,14小题，共70分，把答案填在答题纸指定的横线上)

1、已知，

则

2、　　　

3、已知，，那么的值是　　　　

4、求值　　　　

5、函数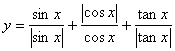的值域是　　　

6、是偶函数，且在是减函数，则整数的值是1,3

7、已知函数在在上是减函数，则实数a的取值范围为[5，+∞]

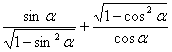8、若角的终边落在直线上，则的值等于　　　　

9、若动直线与函数和的图像分别交于两点，则的最大值为　　　　

10、函数的最小正周期为　　　　 

11、已知函数,则的值域是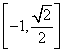

12、不等式恒成立，则x的取值范围是

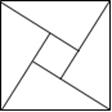13、2007年在北京召开的国际数学家大会，会标是以我国古代数学家赵爽的弦图为基础设计的．弦图是由四个全等直角三角形与一个小正方形拼成的一个大正方形（如图）．如果小正方形的面积为1，大正方形的面积为25，直角三角形中较小的锐角为，那么的值等于

 

14、给出下列命题：①存在实数，使；②若是第一象限角，且，则；③函数是偶函数；④函数的图象向左平移个单位，得到函数的图象．其中正确命题的序号是③

二、解答题：本大题6小题，共90分，解答应写出文字说明、证明过程或演算步骤，并将解答过程写在指定的方框内）

15、已知，

（1）求的值；

（2）求函数的最大值．

解：（1）由

得，

于是=.　　　　　

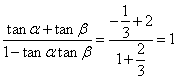（2）因为

所以　　　　　

　　　

的最大值为.　　　

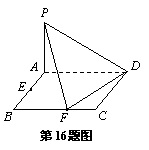16、已知ABCD是矩形，，E、F分别是线段AB、BC的中点，面ABCD.

(1) 证明：PF⊥FD；

(2) 在PA上找一点G，使得EG∥平面PFD.

解：(1) 证明：连结AF，

∵在矩形ABCD中，，F是线段BC的中点，∴AF⊥FD.

又∵PA⊥面ABCD，∴PA⊥FD.　∴平面PAF⊥FD.　∴PF⊥FD.　

(2) 过E作EH∥FD交AD于H，则EH∥平面PFD且.

再过H作HG∥DP交PA于G，则HG∥平面PFD且.

∴平面EHG∥平面PFD.　∴EG∥平面PFD.　 从而满足的点G为所找.

17、已知圆满足：（1）截y轴所得弦长为2，（2）被x轴分成两段弧，其弧长的比为3：1，（3）圆心到直线：x-2y=0的距离为，求这个圆方程．

解：设所求圆圆心为P（a,b），半径为r，则点P到x轴、y轴的距离分别为b、a，

由题设知圆P截x轴所对劣弧对的圆心角为90⁰，知圆P截x轴所得弦长为r，故r²=2b², 又圆P被 y轴所截提的弦长为2，所以有r²=a²+1，从而2b²-a²=1.　又因为P（a,b）到直线x-2y=0的距离为，

所以d==，即a-2b=1,　　解得a-2b=1,

由此得,

于是r²=2b²=2, 所求圆的方程是(x+1)²+(y+1)²=2或(x-1)²+(y-1)²=2.

18、已知

　 （Ⅰ）若分别求的值；

　 （Ⅱ）试比较的大小，并说明理由.

解：（Ⅰ）∵

∴

又　∴

∴

　（Ⅱ）∵，∴

又上为减函数，∴

19、已知定义在R上的函数f(x)=的周期为，且对一切xR，都有f(x)；（1）求函数f(x)的表达式；（2）若g(x)=f(),求函数g(x)的单调增区间；

解：(1)∵，又周期 ∴

　∵对一切xR，都有f(x)　∴ 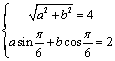解得：

∴的解析式为

（2）　  ∵

∴g(x)的增区间是函数y=sin的减区间　 ∴由得g(x)的增区间为 （等价于

20、已知是方程的两个不等实根，函数的定义域为。

（1）判断函数在定义域内的单调性，并证明。

（2）记：，若对任意，恒有成立，

求实数a 的取值范围。

证一：设　　

则

又

故在区间上是增函数。　　　　　　　　　　　　　　　　

证二：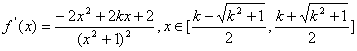

易知：当

故在区间上是增函数。

（2）解：恒成立。