高三文科数学上册周周练二
命题人:项正宏 2009-07-29
一、填空题:本大题共14小题,每小题5分,共70分.
1. 若椭圆![]() (0<m<1)的离心率为
(0<m<1)的离心率为![]() ,则它的长轴长为 ▲
,则它的长轴长为 ▲
 2、定义运算
2、定义运算![]() ,则符合条件
,则符合条件![]() =0的复数z的共轭复数所对应的点在 ▲ 象限
=0的复数z的共轭复数所对应的点在 ▲ 象限
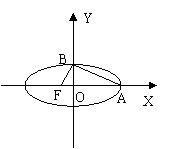
3、如图,椭圆中心在坐标原点,F为左焦点,当![]() 时,
时,
其离心率为![]() ,此类椭圆称为“黄金椭圆”.类比“黄金椭圆”
,此类椭圆称为“黄金椭圆”.类比“黄金椭圆”
可推算出“黄金双曲线”的离心率e等于 ▲
4、由直线y=x+1上的一点向圆(x-3)2+y2=1引切线,则切线长的最小值是 ▲
5、若关于![]() 的不等式
的不等式![]() 的解集是
的解集是![]() ,则实数
,则实数![]() 的值是 ▲
的值是 ▲
 6、定义在区间
6、定义在区间![]() 内的函数
内的函数![]() 满足
满足![]() ,则
,则![]() 的解析式为 ▲ ;
的解析式为 ▲ ;
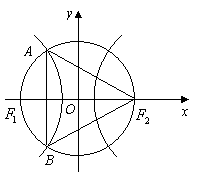
7、如图,![]() 和
和![]() 分别是双曲线
分别是双曲线![]()
的两个焦点,![]() 和
和![]() 是以
是以![]() 为圆心,以
为圆心,以![]() 为半径的圆与
为半径的圆与
该双曲线左支的两个交点,且![]() 是等边三角形,则双
是等边三角形,则双
曲线的离心率为 ▲
8. 已知双曲线![]() 的一条渐近线与直线
的一条渐近线与直线![]() 垂直,则该双曲线的准线方程是 ▲
垂直,则该双曲线的准线方程是 ▲
9、方程![]() 所表示的曲线是 ▲
所表示的曲线是 ▲
10、![]() 的焦点坐标是_____▲____。
的焦点坐标是_____▲____。
11、当![]() 时,函数
时,函数![]() 的最小值是 ▲
的最小值是 ▲
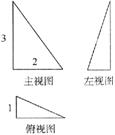
12、一个空间几何体的主视图、左视图、俯视图为直角三角形,边长如图所示,那么这个几何体的体积为 ▲
13、2007年10月30日,嫦娥一号卫星飞行至48小时轨道远地点,距离地面m(=12.8万)公里,创下中国航天器到达的最远距离纪录, 近地点距地面为![]() (=7万)公里,地心在椭圆轨道的一个焦点上, 地球半径为r公里, 则卫星运行48小时椭圆轨道的短半轴长为
(=7万)公里,地心在椭圆轨道的一个焦点上, 地球半径为r公里, 则卫星运行48小时椭圆轨道的短半轴长为
▲ (用m,n,r表示).
.
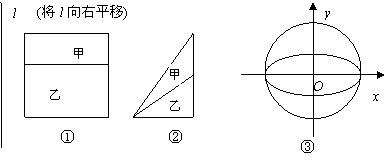
14、我们可以运用下面的原理解决一些相关图形的面积问题:如果与一固定直线平行的直线被甲、乙两个封闭的图形所截得线段的比都为k,那么甲的面积是乙的面积的k倍.你可以从给出的简单图形①、②中体会这个原理.现在图③中的曲线分别是![]() 与
与![]() ,运用上面的原理,图③中椭圆的面积为
▲ .
,运用上面的原理,图③中椭圆的面积为
▲ .
二、解答题
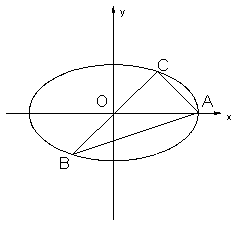 15、如图,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且
15、如图,已知A、B、C是长轴长为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且![]() ·
·![]() =0,
=0,![]() ,求椭圆的方程;
,求椭圆的方程;
1. 16、已知定义域为![]() 的函数
的函数![]() 是奇函数。
是奇函数。
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)若对任意的![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围;
的取值范围;
17、(本题满分15分)设椭圆C:![]() 的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且
的左焦点为F,上顶点为A,过点A与AF垂直的直线分别交椭圆C与x轴正半轴于点P、Q,且![]() .
.
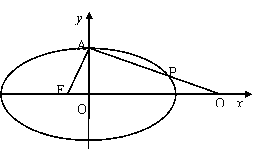 ⑴求椭圆C的离心率; ⑵若过A、Q、F三点的圆恰好与直线l:
⑴求椭圆C的离心率; ⑵若过A、Q、F三点的圆恰好与直线l:![]() 相切,求椭圆C的方程.
相切,求椭圆C的方程.
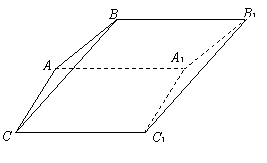
18、如图,斜三棱柱![]() 中,面
中,面![]() 是菱形,
是菱形,![]() ,侧面
,侧面
![]()
![]() ,
,![]() .
.
求证:(1)![]()
![]() ;
;
(2)求点![]() 到平面
到平面![]() 的距离.
的距离.
19、已知点![]() ,抛物线
,抛物线![]() . 过点
. 过点![]() 作直线
作直线![]() ,交
,交
抛物线![]() 于点
于点![]() 、
、![]() . 如果以线段
. 如果以线段![]() 为直径的圆过抛物线
为直径的圆过抛物线![]() 的顶点,求直线
的顶点,求直线![]()
的方程.
20、已知圆O:![]() 交
交![]() 轴于A,B两点,曲线C是以
轴于A,B两点,曲线C是以![]() 为长轴,离心率为
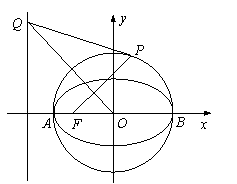
为长轴,离心率为![]() 的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.
的椭圆,其左焦点为F.若P是圆O上一点,连结PF,过原点O作直线PF的垂线交椭圆C的左准线于点Q.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若点P的坐标为(1,1),求证:直线PQ与圆![]() 相切;
相切;
(Ⅲ)试探究:当点P在圆O上运动时(不与A、B重合),直线PQ与圆O是否保持相切的位置关系?若是,请证明;若不是,请说明理由.
08-09文科周周练二答案
1、4
2、一 3、![]() 4、
4、![]() 5、1 6、
5、1 6、![]() 7、
7、![]() 8.
8.![]()
9、椭圆 10、(0,1/8)
11、—3 12、1
13、![]() 14、
14、![]()
15、答案:(1)A(2,0),设所求椭圆的方程为:
![]() =1(0<b<2), 由椭圆的对称性知,OC=OB,由
=1(0<b<2), 由椭圆的对称性知,OC=OB,由![]() ·
·![]() =0得,AC⊥BC,
=0得,AC⊥BC,
∵BC=2AC,∴OC=AC,∴△AOC是等腰直角三角形,∴C的坐标为(1,1).
∵C点在椭圆上,∴![]() =1,∴b2=
=1,∴b2=![]() .所求的椭圆方程为
.所求的椭圆方程为![]() =1.
=1.
16、解:(Ⅰ)因为![]() 是奇函数,所以
是奇函数,所以![]() =0,即
=0,即![]()
又由f(1)= -f(-1)知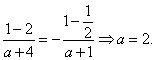
(Ⅱ)由(Ⅰ)知![]() ,易知
,易知![]() 在
在![]() 上
上
为减函数。又因![]() 是奇函数,从而不等式:
是奇函数,从而不等式: ![]()
等价于![]() ,因
,因![]() 为减函数,由上式推得:
为减函数,由上式推得:
![]() .即对一切
.即对一切![]() 有:
有:![]() ,
,
从而判别式![]()
17、⑴解:设Q(x0,0),由F(-c,0)![]() A(0,b)知
A(0,b)知![]()
![]() 设
设![]() ,
,
得![]() 因为点P在椭圆上,所以
因为点P在椭圆上,所以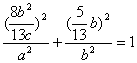
整理得2b2=3ac,即2(a2-c2)=3ac,![]() ,故椭圆的离心率e=
,故椭圆的离心率e=![]()
⑵由⑴知![]() ,
, ![]() 于是F(-
于是F(-![]() a,0) Q
a,0) Q![]() ,
,
△AQF的外接圆圆心为(![]() a,0),半径r=
a,0),半径r=![]() FQ=a
FQ=a
所以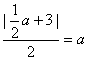 ,解得a=2,∴c=1,b=
,解得a=2,∴c=1,b=![]() ,所求椭圆方程为
,所求椭圆方程为![]()
18、证:(1)设![]() 中点为
中点为![]() ,连
,连![]() 、
、![]() .
.
| |
![]() ,所以
,所以![]() 面
面![]() .
.
又![]() 为正三角形,
为正三角形,![]() ,所以
,所以 ![]()
(2) 由(1),有![]() ,
,![]() ,
,![]() 面
面![]() .设
.设![]() 到面
到面![]() 的
的
距离为![]() ,则
,则
|

![]() 因为
因为![]() ,
,
|
|
|
![]() .
.
设![]() 的高为
的高为![]() ,则
,则![]() ,
,
![]() ,
, ![]() .
.
于是有 ![]() ,即
,即![]() 到平面
到平面![]() 的距离为
的距离为![]() .
.
19、解: 如果直线![]() 过原点,显然满足要求,此时方程为
过原点,显然满足要求,此时方程为
![]() . (1)
. (1)
如果直线![]() 不过原点,设其方程为
不过原点,设其方程为
![]() .
(2)
.
(2)
又设![]() 、
、![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,则
,则
![]() .
(3)
.
(3)
因为![]() ,所以得
,所以得
![]() . (4)
. (4)
由方程 ![]() 消去
消去![]() 得
得
![]() , (5)
, (5)
由韦达定理得
![]() ,
(6)
,
(6)
所以
![]() ,
(7)
,
(7)
故所求方程为
![]() . (8)
. (8)
由于![]() ,所以
,所以![]() ,即方程(5)的常数项为负,从而判别式大于
,即方程(5)的常数项为负,从而判别式大于
![]() ,(5)一定有解
,(5)一定有解![]() . 故(8)符合题意.
. 故(8)符合题意.
20、解:(Ⅰ)因为![]() ,所以c=1
,所以c=1
则b=1,即椭圆![]() 的标准方程为
的标准方程为![]()
 (Ⅱ)因为
(Ⅱ)因为![]() (1,1),所以
(1,1),所以![]() ,所以
,所以![]() ,所以直线OQ的方程为y=-2x
,所以直线OQ的方程为y=-2x
又椭圆的左准线方程为x=-2,所以点Q(-2,4)
所以![]() ,又
,又![]() ,所以
,所以![]() ,即
,即![]() ,
,
故直线![]() 与圆
与圆![]() 相切
相切
(Ⅲ)当点![]() 在圆
在圆![]() 上运动时,直线
上运动时,直线![]() 与圆
与圆![]() 保持相切证明:设
保持相切证明:设![]() (
(![]() ),则
),则![]() ,所以
,所以![]() ,
,![]() ,
,
所以直线OQ的方程为![]() 所以点Q(-2,
所以点Q(-2,![]() )
)
所以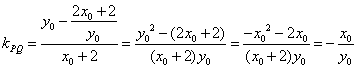 ,又
,又![]() ,
,
所以![]() ,即
,即![]() ,故直线
,故直线![]() 始终与圆
始终与圆![]() 相切
相切