2008届高三文科数学第二轮复习资料
——《不等式》专题
1．有一批DVD机原销售价为每台800元，在甲、乙两家商场均有销售．甲商场用如下的方法促销：买一台单价为780元，买两台每台单价都为760元，依此类推，每多买一台则所买各台单价均再减少20元，但每台最低不能低于440元；乙商场一律都按原价的75％销售．某单位需购买一批此类DVD机，问去哪家商场购买花费较少？
2．某商场预计全年分批购入每台价值为2000元的电视机共3600台，每批都购入
台（是自然数），且每批均需付运费400元，贮存购入的电视机全年所付保管费与每批购入电视机的总价值（不含运费）成正比，若每批购入400台，则全年需用去运输和保管总费用43600元，现在全年只有24000元资金可以用于支付这笔费用，请问：能否恰当安排每批进货的数量使资金够用？写出你的结论，并说明理由．
3． 某公司承担了每天至少搬运280吨水泥的任务，已知该公司有6辆A型卡车和4辆B型卡车，又知A型卡车每天每辆的运输量为30吨，成本费为0.9千元，B型卡车每天每辆的运输量为40吨，成本费为1千元．设每天派出A型卡车辆，B型卡车
辆，公司每天所花成本费
千元，求的最小值，并求此时
的值．
4. 已知函数
（a，b为常数）且方程f(x)－x+12=0有两个实根为x1=3, x2=4.
（1）求函数f(x)的解析式；
（2）设k>1，解关于x的不等式；
.
5．已知
，
．
（Ⅰ）当
时，求证：
在
上是减函数；
（Ⅱ）如果对
不等式
恒成立，求实数
的取值范围
6．已知是奇函数，且在定义域（－1，1）内可导，并满足
，解关于m的不等式
.
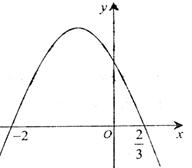
7．设
的极小值为
，其导函数
的图像经过点
，
，如图所示.
（Ⅰ）求的解析式；
（Ⅱ）若对
都有
恒成立，求实数
的取值范围.
8．已知定义在R上的函数
是实数.
（Ⅰ）若函数在区间
上都是增函数，在区间（－1，3）上是减函数，并且
求函数的表达式；
（Ⅱ）若
，求证：函数是单调函数．
9．命题p：方程
有一正根和一负根．
命题q：函数 轴有公共点．
若命题“ ”为真命题，而命题“ ”为假命题，求实数 的取值范围
10．已知二次函数满足
，且
对于
恒成立．
（Ⅰ）求
的值；
（Ⅱ）求的解析式；
（Ⅲ）设
，定义域
，现给出一个数字运算程序：
，若
，运算继续下去；若
，则停止运算．现给出
，请写出满足上述条件的集合
．
参考答案
1． 解：设某单位购买台DVD机，甲、乙两商场的购货款的差价为元，则去甲商场购买总花费
，据题意，
，∴
，
去乙商场购买总花费
，
，
∴
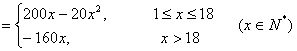
得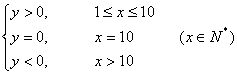
∴买少于10台，去乙商场花费较少；若买10台，去甲、乙商场花费一样；若买超过10台，去甲商场花费较少．
2． 解：设每批购入台，需进货
次，每批进货总价值
，全年保管费
，
依题意：
，∴
，
，
当且仅当
＝
，
，即
台，
答：每批进货的数量为120台时能使资金够用．
3． 解：由题意得：
约束条件：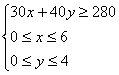
，
目标函数
，
作图得：当
时，
．
4. （1）将
得
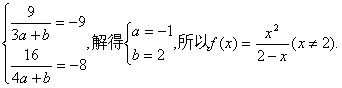
（2）不等式即为
即
①当
②当
③
.
5. 解：（Ⅰ）当时，
∵
∴在上是减函数
Ⅱ）∵不等式恒成立
即不等式
恒成立
∴不等式
恒成立
当
时， 
不恒成立
当
时，不等式恒成立
即
∴
综上所述，的取值范围是
．
6.解：
是减函数.
又由
7. 解：（1）
，且
的图象过点
∴
，
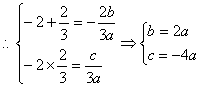
由图象可知函数
在
上单调递减，
在 
上单调递增，在
上单调递减，
∴
，即
，解得
∴
（2）要使对
都有成立，只需
由（1）可知函数在
上单调递减，在上单调递增，
在
上单调递减，且
，
∴
故所求的实数m的取值范围为
8.解（1）
由
又由于在区间上是增函数，在区间（－1，3）上是减函数，所以－1和3必是
的两个根.
从而
又根据
（2）
因为
为二次三项式，并且
，
所以，当
恒成立，此时函数是单调递增函数；
当
恒成立，此时函数是单调递减函数.
因此，对任意给定的实数a，函数总是单调函数.
9.解：
命题“
”为真命题，而命题“
”为假命题，
“p真q假”或“p假q真”
当“p真q假”时，
得1< <5
当“p假q真”时，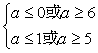
得
综上，的取值范围是：
10．解：（Ⅰ）依题意，有
．
（Ⅱ）设
，则
，
又因为
对任意的恒成立，故
，即的解析式为
．
（Ⅲ）由（Ⅱ）得
．
依题意，当时，有
，
，
，
无意义，
故
．