2008届高三文科数学第二轮复习资料
——《函数与导数》专题
1.设![]() 是定义在
是定义在![]() 上的函数,对一切
上的函数,对一切![]() 均有
均有![]() ,且当
,且当![]() 时,
时,![]() ,求当
,求当![]() 时,
时,![]() 的解析式.
的解析式.
2. 已知定义域为![]() 的函数
的函数![]() 是奇函数.(Ⅰ)求
是奇函数.(Ⅰ)求![]() 的值;(Ⅱ)若对任意的
的值;(Ⅱ)若对任意的![]() ,不等式
,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
3.集合A是由适合以下性质的函数f(x)组成的:对于任意的x≥0,f(x)∈(1,4],且f(x)在[0,+∞)上是减函数.
(1)判断函数f![]() (x)=2-
(x)=2-![]() 及f
及f![]() (x)=1+3·(
(x)=1+3·(![]() (x≥0)是否在集合A中?若不在集合A中,试说明理由;
(x≥0)是否在集合A中?若不在集合A中,试说明理由;
(2)对于(1)中你认为是集合A中的函数f(x),不等式f(x)+f(x+2)≤k对于任意的x≥0总成立.求实数k的取值范围.
4. 对于函数![]() ,若存在实数
,若存在实数![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点.
的不动点.
(1)当![]() 时,求
时,求![]() 的不动点;
的不动点;
(2)若对于任何实数![]() ,函数
,函数![]() 恒有两个相异的不动点,求实数
恒有两个相异的不动点,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,若![]() 的图象上
的图象上![]() 两点的横坐标是函数
两点的横坐标是函数![]() 的不动点,且直线
的不动点,且直线![]() 是线段
是线段![]() 的垂直平分线,求实数
的垂直平分线,求实数![]() 的取值范围.
的取值范围.
5. 已知函数f(x)=2x3+ax与g(x)=bx2+c的图像都过P(2,0),且在点P处有相同的切线.
(1)求实数a、b、c的值;
(2)设函数F(x)=f(x)+g(x),求F(x)的单调区间.
6.设x=1与x=2是函数f(x) = a lnx + bx2 + x的两个极值点.
(Ⅰ)试确定常数a和b的值;
(Ⅱ)试判断x=1,x=2是函数f(x)的极大值还是极小值,并说明理由.
7. 2005年10月12日,我国成功发射了“神州”六号载人飞船,这标志着中国人民又迈出了具有历史意义的一步.已知火箭的起飞重量M是箭体(包括搭载的飞行器)的重量m和燃料重量x之和.在不考虑空气阻力的条件下,假设火箭的最大速度y关于x的函数关系式为:![]() .当燃料重量为
.当燃料重量为![]() 吨(e为自然对数的底数,
吨(e为自然对数的底数,![]() )时,该火箭的最大速度为4(km/s).
)时,该火箭的最大速度为4(km/s).
(Ⅰ)求火箭的最大速度![]() 与燃料重量x吨之间的函数关系式
与燃料重量x吨之间的函数关系式![]() ;
;
(Ⅱ)已知该火箭的起飞重量是544吨,是应装载多少吨燃料,才能使该火箭的最大飞行速度达到8km/s,顺利地把飞船发送到预定的轨道?
8.某工厂统计资料显示,产品次品率![]() 与日产量x(件)(
与日产量x(件)(![]() )的关系符合如下规律:
)的关系符合如下规律:
| x | 1 | 2 | 3 | 4 | … | 89 |
|
|
|
|
|
| … |
|
又知每生产一件正品盈利![]() 元,每生产一件次品损失
元,每生产一件次品损失![]() 元
元![]()
(Ⅰ)将该厂日盈利额T(元)表示为日产量x(件)的函数;
(Ⅱ)为了获得最大盈利该厂的日产量应定为多少件?(取![]() 计算).
计算).
9. 某厂家拟在2006年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x万件与年促
销费用m万元(m≥0)满足![]() (k为常数),如果不搞促销活动,则该产品的年销售量只能
(k为常数),如果不搞促销活动,则该产品的年销售量只能
是1万件.已知2006年生产该产品的固定投入为8万元,每生产1万件该产品需要投入16万元,厂家
将每年产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资
金,不包括促销费用).
(1)将2006年该产品的利润y万元表示为年促销费用m万元的函数;
(2)该厂家2006年的促销费用投入多少万元时,厂家的利润最大?
10.某厂生产某种零件,每个零件的成本为40元,出厂单价定为60元,该厂为鼓励销售商订购,决定当一次订购量超过100个时,每多订购一个,订购的全部零件的出厂单价就降低0.02元,但实际出厂单价不能低于51元.
(Ⅰ)当一次订购量为多少个时,零件的实际出厂单价恰降为51元?
(Ⅱ)设一次订购量为x个,零件的实际出厂单价为P元,写出函数![]() 的表达式;
的表达式;
(Ⅲ)当销售商一次订购多少件时,该厂获得的利润为6000元?(工厂售出一个零件的利润=实际出厂单价-成本)
11. 甲、乙两公司同时开发同一种新产品,经测算,对于函数f(x)、g(x),当甲公司投入x万元作宣传时,若乙公司投入的宣传费小于f(x)万元,则乙公司对这一新产品的开发有失败的风险,否则没有失败的风险;当乙公司投入x万元作宣传时,若甲公司投入的宣传费小于g(x)万元,则甲公司对这一新产品的开发有失败的风险,否则没有失败的风险.
(Ⅰ)试解释![]() 的实际意义;
的实际意义;
(Ⅱ)设![]() ,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司应投入多少宣传费?
,甲、乙公司为了避免恶性竞争,经过协商,同意在双方均无失败风险的情况下尽可能少地投入宣传费用,问甲、乙两公司应投入多少宣传费?
12. 某汽车生产企业上年度生产一品牌汽车的投入成本为10万元/辆,出厂价为13万元/辆,年销售量为、5000辆.本年度为适应市场需求,计划提高产品档次,适当增加投入成本,若每辆车投入成本增加的比例为x(0<x<1![]() ,则出厂价相应提高的比例为0.7x,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
,则出厂价相应提高的比例为0.7x,年销售量也相应增加.已知年利润=(每辆车的出厂价-每辆车的投入成本)×年销售量.
(Ⅰ)若年销售量增加的比例为0.4x,为使本年度的年利润比上年度有所增加,则投入成本增加的比例x应在什么范围内?
(Ⅱ)年销售量关于x的函数为![]() ,则当x为何值时,本年度的年利润最大?最大利润为多少?
,则当x为何值时,本年度的年利润最大?最大利润为多少?
参考答案
1.解:由![]() 有
有![]() ,
,
当![]() 时,
时,![]() .
.
设![]() ,则由
,则由![]() 得
得![]() ,又
,又![]() ,
,
于是![]() ,
,
故当![]() 时,
时,![]() .
.
2.解:(Ⅰ)因为![]() 是奇函数,所以
是奇函数,所以![]() =0,即
=0,即![]()
又由f(1)= -f(-1)知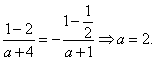
(Ⅱ)由(Ⅰ)知![]() ,易知
,易知![]() 在
在![]() 上为减函数.
上为减函数.
又因![]() 是奇函数,从而有不等式:
是奇函数,从而有不等式:![]()
等价于![]() ,
,
因![]() 为减函数,由上式推得:
为减函数,由上式推得:![]() .
.
即对一切![]() 有:
有:![]() ,从而判别式
,从而判别式![]()
3.解:(1)∵f![]() =2-
=2-![]() =-5
=-5![]() (1,4],∴f
(1,4],∴f![]() 不在集合A中.
不在集合A中.
又∵x≥0, ∴0<(![]() ≤1, ∴0<3·(
≤1, ∴0<3·(![]() ≤3,从而1<1+3·(
≤3,从而1<1+3·(![]() ≤4.∴f
≤4.∴f![]() (x)∈(1,4].
(x)∈(1,4].
又f![]() (x)=1+3·(
(x)=1+3·(![]() 在[0,+∞)上为减函数,∴f
在[0,+∞)上为减函数,∴f![]() (x)=1+3·(
(x)=1+3·(![]() 在集合A中.
在集合A中.
(2)当x≥0时,f(x)+f(x+2)=2+![]() ·(
·(![]() ≤
≤![]() .
.
又由已知f(x)+f(x+2) ≤k对于任意的x≥0总成立, ∴k≥![]() .
.
因此所求实数k的取值范围是[![]() ,+∞).
,+∞).
4.解: ![]() ,
,
(1)当![]() 时,
时,![]() .
.
设![]() 为其不动点,即
为其不动点,即![]() ,则
,则![]() .
.
所以![]() ,即
,即![]() 的不动点是
的不动点是![]() .
.
(2)由![]() 得
得![]() .
.
由已知,此方程有相异二实根,所以![]() ,
,
即![]() 对任意
对任意![]() 恒成立.
恒成立.
![]() ,
,![]() .
.
(3)设![]() ,直线
,直线![]() 是线段
是线段![]() 的垂直平分线,
的垂直平分线,![]() .
.
记![]() 的中点
的中点![]() ,由(2)知
,由(2)知![]() .
.
![]()
![]() 在
在![]() 上,
上,![]()
化简得: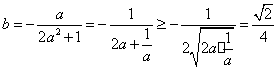 ,当
,当![]() 时,等号成立.
时,等号成立.
即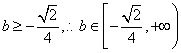
5.解:(1)∵f(x),g(x)的图像过P(2,0)∴f(2)=0即2×23+a×2=0,所以a=-8.
g(2)=0 即:4×b+c=0
又∵f(x),g(x)在P处有相同的切线,∴4b=16,b=4,c=-16,
∴a=-18,b=4,c=-16.
(2)由F(x)=2x3+4x2-8x-16,有F′(x)=6x2+8x-8
解不等式F′(x)=6x2+8x-8≥0得x≤-2或x≥![]() 即单调增区间为
即单调增区间为![]() .
.
同理,由F′(x)≤0得-2≤x≤![]() ,即单调减区间为[-2,
,即单调减区间为[-2,![]() ].
].
6.解:(Ⅰ)f′(x)=![]() +2bx+1,由极值点的必要条件可知:f′(1)=f′(2)=0,即a+2b+1=0, 且
+2bx+1,由极值点的必要条件可知:f′(1)=f′(2)=0,即a+2b+1=0, 且![]() +4b+1=0,
+4b+1=0,
解方程组可得a=-![]() ,b=-
,b=-![]() ,∴f(x)=-
,∴f(x)=-![]() lnx-
lnx-![]() x2+x.
x2+x.
(Ⅱ)f′(x)=-![]() x-1-
x-1-![]() x+1,
x+1,
当x∈(0,1)时,f′(x)<0,
当x∈(1,2)时,f′(x)>0,
当x∈(2,+∞)时,f′(x)<0,
故在x=1处函数f(x)取得极小值![]() , 在x=2处函数取得极大值
, 在x=2处函数取得极大值![]() -
-![]() ln2.
ln2.
7.解:(Ⅰ)依题意把![]() 代入函数关系式
代入函数关系式
![]()
所以所求的函数关系式为![]() 整理得
整理得![]()
(Ⅱ)设应装载x吨燃料方能满足题意,此时,![]() ,
,
代入函数关系式![]()
即应装载344吨燃料方能顺利地把飞船发送到预定的轨道.
8.解:(Ⅰ)由![]() 与x的对应规律得次品率为
与x的对应规律得次品率为![]()
故日产量x件中,次品数为![]() 件,正品数为
件,正品数为![]() 件.
件.
则日盈利额![]() .
.
(Ⅱ)![]()
(注:此步可由换元法令![]() 得到)
得到)
![]()
当且仅当![]() 时取等号.
时取等号.
由![]()
![]() 时,
时,![]() 取得最小值,
取得最小值,
又![]() ,
,![]() ,
,
因此,要获得最大盈利,该厂的日产量应定为83件.
9.解(1)由题意可知当![]() 时,
时,![]() (万件)
(万件)
![]()
![]()
每件产品的销售价格为![]() (元)
(元)
![]()
![]() …
…
![]()
(2)![]()
![]() (万元)时,
(万元)时,![]() (万元)
(万元)
所以该厂家2006年的促销费用投入3万元时,厂家的利润最大,最大值为21万元.
10.解:(1)设每个零件的实际出厂价恰好降为51元时,一次订购量为![]() 个,则
个,则![]()
因此,当一次订购量为550个时,每个零件的实际出厂价恰好降为51元.
(2)当![]()
当![]()
![]()
当![]()
所以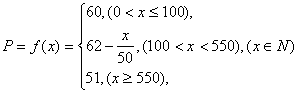
(3)设销售商的一次订购量为x个时,工厂获得的利润为L元,则
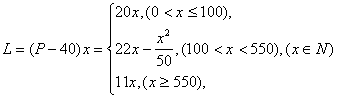
由于当![]() ;
;![]()
所以,![]() 此时
此时![]()
由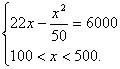 解得
解得![]() .
.
因此,当销售商一次订购500个零件时,该厂获得利润6000元.
11.解:(I)f(0)=10表示当甲公司不投入宣传费时,乙公司要避免新产品的开发有失败风险,至少要投入10万元宣传费;g(0)=20表示当乙公司不投入宣传费时,甲公司要避免新产品的开发有失败的风险,至少要投入20万元宣传费.
(Ⅱ)设甲公司投入宣传费x万元,乙公司投入宣传费y万元,依题意,当且仅当
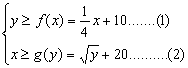 成立,双方均无失败的风险.
成立,双方均无失败的风险.
由(1)(2)得![]()
![]()
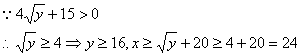
![]()
答:要使双方均无失败风险,甲公司至少要投入24万元,乙公司至少要投入16万元.
12. 解:(I)由题意得:本年度每辆车的投入成本为10×(1+x);出厂价为13×(1+0.7x); 年销售量为5000×(1+0.4x).因此本年度的利润为
![]()
![]()
(Ⅱ)本年度的利润为
![]()
则![]()
由![]()
当![]() 是增函数;
是增函数;
当![]() 是减函数.
是减函数.
∴当![]() 时,
时,![]() 万元,
万元,
因为f(x)在(0,1)上只有一个极大值,所以它是最大值.
即当![]() 时,本年度的年利润最大,最大利润为20000万元.
时,本年度的年利润最大,最大利润为20000万元.