高三年级文科数学上册第二次月考试题
数学试题（文科）
一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.
1、 已知集合
，
，则
( )
A .
； B .
； C .
；
D .
2、 函数
的定义域是
( )
A .
； B .
； C
.
； D .（－1，0）
3、 若把函数
的反函数记为
，则
( )
A .
；
B .2； C .
；
D . 
4.已知函数
，则
( )
A .0；
B .1；
C .3；
D .
5、 二次函数
在
上是减函数，则实数
的取值范围是
( )
A .
； B .
； C .
； D .
6、已知映射
,其中
,
,对应法则为
；对于
,但在集A中找不到原像,则实数
的取值范围为
( )
A .
;
B .
;
C .
; D .
7.函数f(x)=log3x+2(x>9)，则f(x)的值域是： ( )
A．（2，+
） B。（3，+） C。（4，+） D。[4，+]
8.设f(x)是（－，+）上的奇函数，f(x+2)=－f(x)，当0≤x≤1时，f(x)=x，则f(7.5)等于：
( )
A。0.5 B。－0.5 C。1.5 D。－1.5
9.已知镭经过100年剩余量为原来的95.76%，设质量为1的镭经过x年后和剩余量为y，那么x,y之间的函数关系是： ( )
A．y=(0.9576)100x B. 
C.y=1－
D. 
10．若对某校1200名学生的耐力作调查，抽取其中的120名学生，测试他们1500米跑的成绩，得出相应的数值，在这项调查中，样本是指： ( )
A．120名学生 B。1200学生 C。120名学生的成绩 C。1200名学生的成绩
11.若曲线y=x2－1与y=1－x3在x=x0处的切线互相垂直，则x0的值为： ( )
A．
B。
C。－ D。－或0
12.已知不等式x4+4x2>2－a对任意实数x 都成立，那么a的取值范围是： ( )
A．a>2 B.a>6 C.a为一切实数 D。这样的a不存在
彭山二中高三年级第二次月考
数学试题（文科）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
二．填空题（共4小题，每小题4分）
13.．设f(x)是定义在R上的奇函数，且y=f(x)的图象关于直线
对称，则f(1)+f(2)+f(3)+f(4)+f(5)=________________；
14.设函数
，则函数
的定义域为__________
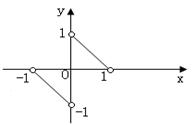
15．已知函数
的图象如图，则不等式
的解集为
.
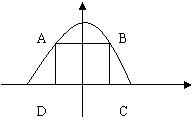16.如图，内接于抛物线y=1－x2的矩形ABCD，其中A，B在抛物线上运动，则此矩形的面积最大值为_____________。
三．解答题（本大题共6个小题，共74分）
17．（本小题满分12分）设函数
的定义域为A，若命题
有且只有一个为真命题，求实数a的取值范围.
18．（本小题满分12分）已知函数＝
，
（a为正常数），
且函数与
的图象在y轴上的截距相等．
（１）求a的值； （２）求函数－的单调递增区间．
19、（12分）利民商店经销各种洗衣粉,年销售总量为6000包,每包进价2..8元,销售价3.4元,全年分若干次进货,每次进货
包,,已知每次进货运输劳务费为62.5元,全年保管费为1.5元.
⑴该商店经销洗衣粉一年的利润
(元)表示为每次进货量包的函数,并指出函数的定义域.
⑵为了使利润最大,每次应进多少包?
20.（12分）偶函数f(x)=ax4+bx3+cx2+dx+e的图象过点P（0，1），且在x=1处的切线方程为y=x－2。 （1）求y=f(x)的解析式；（2）求y=f(x)的极值。
21. （本题满分12分）已知a为实数，
（Ⅰ）求导数
；
（Ⅱ）若
，求在[－2，2] 上的最大值和最小值；
（Ⅲ）若在（—∞，—2]和[2，+∞）上都是递增的，求a的取值范围.
22、（14分）已知函数
为自然对数的底数
，
①（3分）判断函数
的奇偶性。
②（3分）若
，求常数的值与函数
的表达式。
③（4分）求证：
。
④（4分）求函数的反函数。
参考答案（文科）
| D | C | C | B | A | A | C | B | B | C | B | A |
13.0 
(－2,－1)È(1,2) 15． 
16.
17．解：
…………1分
若
…………3分
若
…………5分
若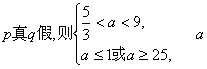
无解； …………8分
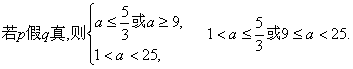…………11分
综上，
…………12分
18．（１）由题意
，
＝１又a＞０，所以a＝１．………………… 4分
（２）
g（x）＝
，…………………………………… 5分
当
时，
＝
，无递增区间；………………………… 7分
当x＜１时，＝
，它的递增区间是
．………… 10分
综上知：的单调递增区间是．…………………………… 12分
19. 解：①设“两次点数相同”为事件
，则
。（6分）
②设“两次点数之和为4”为事件
，则
。（6分）
20.（1）f(x)偶函数，则b=d=0，又图象过点P（0，1），则e=1，这时f(x)=ax4+cx2+1，y’=4ax3+2cx，故4a+2c=1，又切线的切点（1，－1）在曲线上，a+c+1=－1，得a=
,c=
F(x)= x4x2+1
(2)f’(x)=10x3－9x,令f’(x)=0得x=0或x=
通过列表得x=时f(x)极小为
，当x=0时，f(x)极大值=1.
21 解: (Ⅰ)由原式得
∴
(Ⅱ)由 得
,此时有
.
由得
或x=－1 , 又
所以f(x)在[－2,2]上的最大值为
最小值为
(Ⅲ)解法一: 
的图象为开口向上且过点(0,－－4)的抛物线,由条件得
即
∴－2≤a≤2.
所以a的取值范围为[－2,2].
解法二:令
即
由求根公式得: 
所以在
和
上非负.
由题意可知,当x≤－2或x≥2时, ≥0,
从而x1≥－2, x2≤2,
即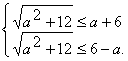
解不等式组得: －2≤a≤2.
∴a的取值范围是[－2,2].
22题（ 14分）：解：① 
的定义域为
关于原点对称，
为奇函数。（3分）
② 
又，
，
。（6分）
③ 解一、由②知
，
，
，
，
，即
，
。（10分）
解二、设
，则
，
，
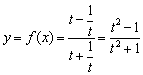。（10分）
解三、由②知，
，（10分）
④ 由②知，
，
，
的反函数为
。（14分）