高三年级理科数学上册第二次月考试题
数学试题（理科）
一、选择题（本大题共12小题，每小题5分，共60分）
1．集合
= （ ）
A．
B．{1} C．{0,1,2} D． {－1,0,1,2}
2．已知集合
，集合B={xx>a}，若A∩B=
，则a的取值范围是：
A．
B．a≥1
C．a<1 D． 
3.点M(x, y)在映射“f”下的象是N(x＋2y, 3x－4y)，则在此映射下点(5, 6)的象是（ ）。
（A）(5, 6) （B）(17, －9) （C）(
, 
)
（D）其它答案
4．函数
的图像是： （ ）
A
B
C
D
5. 
（ ）
A．
B．－ C．
D．－
6.命题“若A∩B=A，则A∪B=B”的逆否命题是： （ ）
A．若A∪B=B，则A∩B=A B。若A∩B≠A，则A∪B≠B
C．若A∪B≠B，则A∩B≠A D。若A∩B≠B，则A∪B≠A
7.一个容量为20的样本,已知某组的频率为0.25,则该组的频数为 （ ）
A．２ Ｂ．５ Ｃ．１５ Ｄ．８０
8.数列{an}中，a1=
，an+an+1=
（n∈N+），则
（a1+a2+…+an）=
A.
B.
C.
D.
9.若f(n)=1+
（n∈N+），那么n=1时，f(n)为： （ ）
A．1 B。
C。
D。以上都不对
10.
（ ）
A．
B．
C．
D．
11．已知
（
是常数），在
上有最大值3，那么在上的最小值是 （ ）
A．
B．
C．
D．
12.从一批含有13只正品、2只次品的产品中，不放回地抽取3次，每次抽取一只，设抽得次品数为
，则E（5+1）= ( )
A。3 B。2 C。1 D。2.5
彭山二中高三年级第二次月考
数学试题（理科）
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
二、填空题（每题4分，共16分）
１３．已知
是周期为２的奇函数，当
时，
设
则
的大小关系为
14. 样本（0，2，4，6，8）是随机地从总体M中抽取的，则总体的方差是______
15.若曲线y=x3－2x+a与直线y=3x+1相切，则常数a的值为___________.
16.给出下列四个命题：（1）若函数f(x)=
，则
；（2）若函数f(x)=2x2+1图象上点（1，3）的邻近一点为（1+
x,3+y），则
；（3）瞬时速度是动点位移函数s(t)对时间t的导数；（4）曲线y=x3在点（0，0）处没有切线。其中正确的命题有________.
三．解答题（本大题共6小题）
17．（本小题满分12分）设函数
的定义域为A，若命题
有且只有一个为真命题，求实数a的取值范围.
18 （本题满分12分）（Ⅰ）已知函数f(x)=
，试求f(x)及其定义域并画出图象；
（Ⅱ）已知函数f(x)=
，指出其不连续点，并补充定义，使其在R上是连续函数。
19. （本题满分12分）盒子中有大小相同的球10个，其中标号为1的球3个，标号为2的球4个，标号为5的球3个，第一次从盒子中任取1个球，放回后第二次再任取1个球（假设取到每个球的可能性都相同）.记第一次与第二次取到球的标号之和为.
（Ⅰ）求随机变量的分布列；（Ⅱ）求随机变量的期望
.
20.（本小题满分12分）已知a为实数，
（Ⅰ）求导数
； （Ⅱ）若
，求
在[－2，2] 上的最大值和最小值；
（Ⅲ）若在（—∞，—2）和[2，+∞]上都是递增的，求a的取值范围.
21. （本题满分12分）记函数f(x)=
的定义域为A， g(x)=lg[(x－a－1)(2a－x)]的定义域为B. (1) 求A； (2) 若B
A, 求实数a的取值范围.
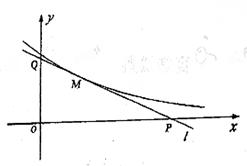
22.（本题满分14分）设曲线
≥0）在点M（t,
）处的切线
与x轴y轴所围成的三角形面积为S（t）.
（Ⅰ）求切线的方程（要求写成一般式）； （Ⅱ）求S（t）的最大值.
高三数学第一次月考答案（理科）
一、选择题（本大题共12小题，每小题5分，共60分）
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | C | A | B | A | A | C | B | C | C | A | D | A |
二、13、
C4 C2，C3
，C1 14、 8 15、 1
16、
(2)(3)
17．解：
………1分 若
………3分
若
…………5分
若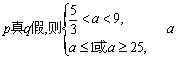
无解； …………8分
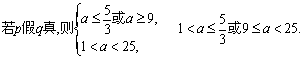…………11分
综上，
…………12分
18.略
19. 解: (Ⅰ)由题意可得,随机变量的取值是2、3、4、6、7、10.
随机变量的概率分布列如下
|
| 2 | 3 | 4 | 6 | 7 | 10 |
| P | 0.09 | 0.24 | 0.16 | 0.18 | 0.24 | 0.09 |
随机变量的数学期望=2×0.09+3×0.24+4×0.16+6×0.18+7×0.24+10×0.09=5.2.
20. 解:
(Ⅰ)由原式得
∴
(Ⅱ)由 得
,此时有
.
由得
或x=－1 , 又
所以f(x)在[－2,2]上的最大值为
最小值为
(Ⅲ)解法一: 
的图象为开口向上且过点(0,－－4)的抛物线,由条件得 
即
∴－2≤a≤2. 所以a的取值范围为[－2,2].
解法二:令
即
由求根公式得: 
所以在
和
上非负.
由题意可知,当x≤－2或x≥2时, ≥0,
从而x1≥－2, x2≤2, 即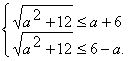
解不等式组得: －2≤a≤2.
21【解】(1)2－
≥0, 得
≥0, x<－1或x≥1
即A=(－∞,－1)∪[1,+ ∞]
(2) 由(x－a－1)(2a－x)>0, 得(x－a－1)(x－2a)<0.
（a）当a<1时，a+1>2a, ∴B=(2a,a+1).
∵BA, ∴2a≥1或a+1≤－1, 即a≥
或a≤－2, 而a<1,∴≤a<1或a≤－2,
（b）当a=1时，B是空集，f(x)意义；（c）当a>1时，B=（a+1,2a）,又 BA，则a+1≥1,∴a≥0故a>1，所以BA时实数a的取值范围是(－∞,－2]∪[,1
1，+∞)。
22解：（Ⅰ）因为
所以切线的斜率为
故切线的方程为
即
.
（Ⅱ）令y=0得x=t+1,
又令x=0得
所以S（t）=
=
从而
∵当
（0，1）时，
>0,
当（1,+∞）时,<0,
所以S(t)的最大值为S(1)=