高三数学复习押题试卷
一、填空题:本大题共14小题,每小题5分,共70分.
 1.
复数
1.
复数![]() ,
,![]() ,则复数
,则复数![]() 在复平面内对应的点位于第______象限.
在复平面内对应的点位于第______象限.
2.在三解形ABC中,![]() 3:2:4,
3:2:4,
则![]() 的值为 .
的值为 .
3. 如图,一个空间几何体的正视图,左视图,俯视
图为全等的等腰直解三角形,如果等腰直角三角
形的直角边长为1,那么这个几何体的体积
为 .
4.下表是某厂1-4月份用水量(单位:百吨)的一
组数据:由其散点图可知用水量![]() 与月
与月
| 月份x | 1 | 2 | 3 | 4 | |
| 水量y | 4.5 | 4 | 3 | 2.5 | |
份![]() 之间有较好的线性相关关系,其线性
之间有较好的线性相关关系,其线性
回归方程![]() 则
则![]() =
=
5. 对于每个实数![]() ,设
,设![]() 是
是![]() ,三个函数中的最小值,则
,三个函数中的最小值,则![]() 的最大值是
。
的最大值是
。
6.一只半径为R的球放在桌面上,桌面上一点A的正上方相距(![]() +1)R 处有一点光源O,OA与球相切,则球在桌面上的投影――椭圆的离心率为 .
+1)R 处有一点光源O,OA与球相切,则球在桌面上的投影――椭圆的离心率为 .
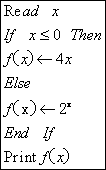 7.设不等式组
7.设不等式组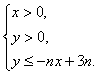 所表示的区域为
所表示的区域为
![]() ,记
,记![]() 内的格点数为
内的格点数为![]() ,则
,则![]() =(格点是
=(格点是
指横没坐标与纵坐标都为整数的点)
8.给出一个算法如下,根据算法,可求得
![]() =
.
=
.
9.“![]() ”是“
”是“![]() ”的 条件.(充分不必要,必要不充分,充分必要,既不充分也不必要).
”的 条件.(充分不必要,必要不充分,充分必要,既不充分也不必要).
 10.已知函数
10.已知函数![]() 如果
如果![]() ,则实数
,则实数![]() 的取值范围是
的取值范围是
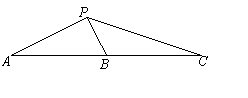
11. A,B,C是直线l上的三点,P是
直线l外一点,已知AB=BC=a,
∠APB=90°,∠BPC=45° ,∠PBA=
q.则·= 。
12.已知三次函数![]()
![]()
![]() ,则
,则![]() .
.
13.观察下列不等式:![]() ≥
≥![]() ,
,![]() ≥
≥![]() ,
,![]() ≥
≥![]() ,…,由此猜测第
,…,由此猜测第![]() 个不等式为
.(
个不等式为
.(![]() )
)
14.已知正方体ABCD-![]() 中,任作一个平面M与对角线
中,任作一个平面M与对角线![]() 垂直,且平面M与正方体的每个面都有公共点,设截面多边形的面积为S,周长为L,现给出下列四个命题:
垂直,且平面M与正方体的每个面都有公共点,设截面多边形的面积为S,周长为L,现给出下列四个命题:
①S为定值;②S不为定值;③L为定值;④L不为定值。其中所有正确命题的序号为_______________.
二、解答题:
15. (本小题共14分)在锐角三角形ABC中,角A,B,C所对的边为![]() ,设向量
,设向量![]() 且
且![]() 共线。
共线。
(1)求角B的取值范围;
(2)当角B取最大值时记![]() ,求
,求![]() 的取值范围.
的取值范围.
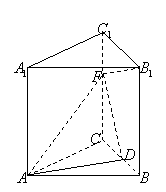 16.
(本小题共14分)25.在直三棱柱
16.
(本小题共14分)25.在直三棱柱![]() 中,
中,
![]() ,
,![]() ,
,![]() 是
是![]() 的中点,
的中点,
![]() 是
是![]() 上一点,且
上一点,且![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求三棱锥![]() 的体积;
的体积;
(3)试在![]() 上找一点
上找一点![]() ,使得
,使得![]() 平面
平面![]() .
.
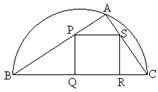
17. (本小题共15分)如图,某园林单位准备绿化一块直径为BC的半圆形空地,
△ABC外的地方种草,△ABC的内接正方形PQRS为一水池,其余的地方种花
.若BC=a,∠ABC=![]() ,设△ABC的面积为S1,正方形的面积为S2.
,设△ABC的面积为S1,正方形的面积为S2.
|
(2)当a固定,![]() 变化时,求
变化时,求![]() 取最小值时的角
取最小值时的角![]()
18.(本小题共15分)设![]() 上的两点,满足
上的两点,满足![]() ,椭圆离心率
,椭圆离心率![]() 短轴长为2,0为坐标原点.
短轴长为2,0为坐标原点.
(1)求椭圆的方程;
(2)若直线AB过椭圆的焦点F(0,c),(c为半焦距),求直线AB的斜率k的值;
(3)试问:△AOB的面积是否为定值?如果是,请给予证明;如果不是,请说明理由.
19.(本小题共16分)已知函数![]()
![]() 且
且![]()
(1)若![]() 在
在![]() 上都有意义,求
上都有意义,求![]() 的取值范围;
的取值范围;
(2)求证:![]() 在
在![]() 上是减函数。
上是减函数。
(3)试问在![]() 上
上![]() 是否恒成立,说明理由。
是否恒成立,说明理由。
20. (本小题共16分)已知正项数列![]() 中,
中,![]() ,点
,点![]() 在抛物线
在抛物线![]() 上;数列
上;数列![]() 中,点
中,点![]() 在过点
在过点![]() ,以方向向量为
,以方向向量为![]() 的直线上。
的直线上。
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)若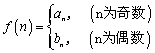 ,问是否存在k∈N*,使
,问是否存在k∈N*,使![]() 成立,若存在,求出
成立,若存在,求出![]() 值;若不存在,说明理由;
值;若不存在,说明理由;
(Ⅲ)对任意正整数![]() ,不等式
,不等式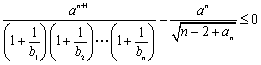 成立,求正数
成立,求正数![]() 的取值范围。
的取值范围。
答案
一、 填空题:
1.一 2. ![]() 3.
3.
![]() .
4.
.
4.
![]() . 5.
3 6.
. 5.
3 6. ![]() 7.6024.
7.6024.
8.
-8.
9. 充要. 10. ![]() .
11. -a2. 12.
1
.
11. -a2. 12.
1
13. ![]() …
…![]() ≥
≥![]() …
…![]() 14. ②③.
14. ②③.
二、解答题:
15.解:(1)由![]() 所以有:
所以有:![]() 因为
因为 ![]() 当且仅当
当且仅当![]() 时取等号)
时取等号)
![]() (2)由(1)知B的最大值为
(2)由(1)知B的最大值为![]() 则A+C=
则A+C=![]() 及正弦定理得:
及正弦定理得:
![]()
![]()
![]() 三角形为锐角三角形
三角形为锐角三角形![]()
![]()
![]()
![]()
16. (1)证明:![]() 为
为![]() 中点
中点 ![]() ,又直三棱柱中:
,又直三棱柱中:![]() 底面
底面![]() 底面
底面![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]()
![]() 平面
平面![]()
![]() .在 矩形
.在 矩形![]() 中:
中:![]() ,
,![]()
![]() ,
,![]()
![]() ,即
,即![]() ,
,
![]() ,
,![]() 平面
平面![]() ;
;
(2)解:![]()
![]() 平面
平面![]()
![]()
=![]() ;
;
(3)当![]() 时,
时,![]() 平面
平面![]() .
.
证明:连![]() ,设
,设![]() ,连
,连![]() ,
,![]()
![]() 为矩形,
为矩形,
![]() 为
为![]() 中点,
中点,![]() 为
为![]() 中点,
中点,![]() ,
,![]() 平面
平面![]() ,
,![]() 平面
平面![]()
![]() 平面
平面![]() .
.
17. 解(1)∵![]()
∴![]()
设正方形边长为x. 则BQ=![]()
![]()
![]()
![]()
(2)当![]() 固定,
固定,![]() 变化时,
变化时,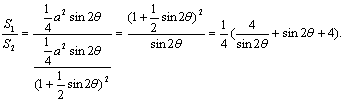
令![]()
![]() 令
令![]() 任取
任取![]() ,且
,且![]() ,
,
![]() .
.
![]() ,
,
![]() 是减函数.
是减函数.![]() 取最小值,此时
取最小值,此时![]()
18. 答案:(1)![]()
椭圆的方程为![]()
(2)设AB的方程为![]()
由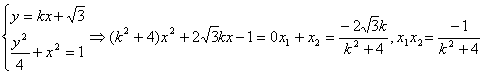
由已知
![]()
![]() 2
2
(3)当A为顶点时,B必为顶点.S△AOB=1
当A,B不为顶点时,设AB的方程为y=kx+b
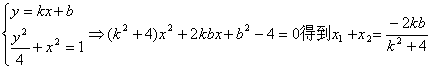
![]()
![]()
![]()
![]()
![]()
所以三角形的面积为定值.
19.解:(1)要使f 1 (x)与f 2 (x)有意义,则有
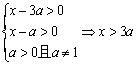 要使f 1 (x)与f 2 (x)在给定区间[a + 2,a + 3]上有意义,等价于真数的最小值大于0
要使f 1 (x)与f 2 (x)在给定区间[a + 2,a + 3]上有意义,等价于真数的最小值大于0
即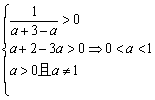
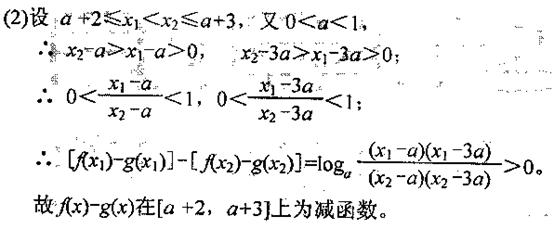

20. 解:(Ⅰ)将点![]() 代入
代入![]() 中得
中得
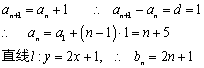
(Ⅱ)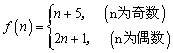

(Ⅲ)由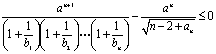
即![]()
记g(n)= ![]()
∴![]()
∴![]()
∴f(n+1)>f(n),即g(n)递增
∴![]()