高三数学复习测试卷(二)
文科《立几、概率与统计、导数》 2008-7-23
一、选择题(5分/题,共计60分,答案填在12题后表中)
1、设![]() 为空间三条直线,下面给出四个命题;①如果
为空间三条直线,下面给出四个命题;①如果![]() ,则
,则![]() ;②如果
;②如果![]() 是异面直线,
是异面直线,![]() 也是异面直线,则
也是异面直线,则![]() 也是异面直线;③如果
也是异面直线;③如果![]() 相交,
相交,![]() 也相交,则
也相交,则![]() 必相交;④如果
必相交;④如果![]() 共面,
共面,![]() 也共面,则
也共面,则![]() 必共面。其中真命题的个数是( )
必共面。其中真命题的个数是( )
A.1 B.2 C.3 D.4
2、甲、乙、丙3位同学选修课程,从4门课程中甲选修2门;乙、丙各选修3门,则不同的选修方案共有( )
A.36种 B.48种 C.96种 D.192种
3、设P为曲线C:![]() 上的点,且曲线C在点P处切线倾斜角的取值范围为
上的点,且曲线C在点P处切线倾斜角的取值范围为![]() ,则点P横坐标的取值范围为( )
,则点P横坐标的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、某交高三年级有男生500人,女生400人,为了解该年级学生的健康情况,从男生中任意抽取25人,从女生中任意抽取20人进行调查.这种抽样方法是 ( )
A.简单随机抽样法 B.抽签法
C.随机数表法 D.分层抽样法
5、从编号为1,2,…,10的10个大小相同的球中任取4个,则所取4个球的最大号码是6的概率为 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6、若函数![]() 在
在![]() 内单调递减,则实数
内单调递减,则实数![]() 的取值范围为( A )
的取值范围为( A )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
7、函数![]() 有极值的充要条件是( )
有极值的充要条件是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、长方体![]() 的各顶点都在半径为1的球面上,其中
的各顶点都在半径为1的球面上,其中![]() ,则两
,则两![]() 点的球面距离为( )
点的球面距离为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
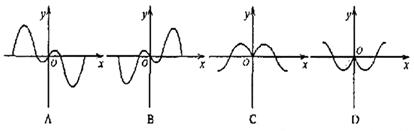
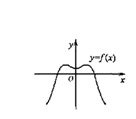 9、如果函数y=f(x)的图象如右图,那么
9、如果函数y=f(x)的图象如右图,那么
导函数![]() 的图象可能是( )
的图象可能是( )
10、已知函数![]() 在区间[-1,2]上是减函数,那么
在区间[-1,2]上是减函数,那么![]() ( )
( )
A.有最大值![]() B.有最大值
B.有最大值![]()
C.有最小值![]() D.有最小值
D.有最小值![]()
11、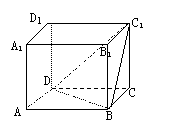 如图长方体中,AB=AD=2
如图长方体中,AB=AD=2![]() ,
,
CC1=![]() ,则二面角C1—BD—C
,则二面角C1—BD—C
的大小为( )
A.30° B.45°
C.60° D.90°
12、某城市拟成立一个由6名大学生组成的社会调查小组,并准备将这6个名额分配给本市的3所大学,要求每所大学都有学生参加,则不同名额分配方法共有( )
A.20种 B.14种 C.10种 D.9种
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | C | A | D | B | A | C | C | A | B | A | C |
二 、填空题(本题共4小题, 4分/题,共计16分)
13、若一个球的体积为![]() ,则它的表面积为
,则它的表面积为 ![]() .
.
14、点P的曲线y=x3-x+上移动,在点P处的切线的倾斜角为α,则α的取值范围![]() .
.
15、已知函数![]() 的图象在点
的图象在点![]() 处的切线方程是
处的切线方程是![]() ,则
,则![]() = 3 .
= 3 .
16、过点![]() 和曲线
和曲线![]() 相切的直线方程为_____
相切的直线方程为_____
![]() 或
或![]() .
.
三、解答题(本题6小题,共计74分)
17、(10分)设集合![]() ,
,![]() 是坐标平面上的点,
是坐标平面上的点,![]() 、
、![]() 。
。
(1)![]() 可以表示多少个坐标平面上的不同的点?
可以表示多少个坐标平面上的不同的点?
(2)![]() 可以表示多少个第二象限内的点?
可以表示多少个第二象限内的点?
(3)![]() 可以表示多少个不在直线
可以表示多少个不在直线![]() 上的点?
上的点?
【解】:(1)36 (2)6 (3)30
18、(12分)已知函数![]() ,且
,且![]() 是奇函数.
是奇函数.
(Ⅰ)求![]() ,
,![]() 的值;(Ⅱ)求函数
的值;(Ⅱ)求函数![]() 的单调区间.
的单调区间.
【解】:(Ⅰ)因为函数![]() 为奇函数,
为奇函数,
所以,对任意的![]() ,
,![]() ,即
,即![]() .
.
又![]()
所以![]() .
.
所以![]()
解得![]() .
.
(Ⅱ)由(Ⅰ)得![]() .
.
所以![]() .
.
当![]() 时,由
时,由![]() 得
得![]() .
.
![]() 变化时,
变化时,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
| + | 0 | _ | 0 | + |
|
|
| 极大值 |
| 极小值 |
|
所以,当![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.
上单调递增.
当![]() 时,
时,![]() ,所以函数
,所以函数![]() 在
在![]() 上单调递增.
上单调递增.
19、(12分)甲、乙、丙三人参加了一家公司的招聘面试,面试合格者可正式签约.甲表示只要面试合格就签约.乙、丙则约定:两人面试都合格就一同签约,否则两人都不签约.设每人面试合格的概率都是![]() ,且面试是否合格互不影响.求:
,且面试是否合格互不影响.求:
(Ⅰ)至少有1人面试合格的概率:
(Ⅱ)没有人签约的概率.
【解】:用A,B,C分别表示事件甲、乙、丙面试合格.由题意知A,B,C相互独立,且P(A)=P(B)=P(C)=![]() .
.
(Ⅰ)至少有1人面试合格的概率是1-P(![]() )
)
=1-![]() .
.
(Ⅱ)没有人签约的概率为
![]()
=![]()
=![]()
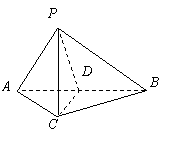
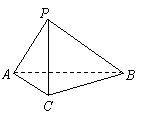 20、(12分)如图,在三棱锥
20、(12分)如图,在三棱锥![]() 中,
中,
![]() ,
,![]() ,
,
![]() ,
,![]() .
.
(Ⅰ)求证:![]() ;
;
(Ⅱ)求二面角![]() 的大小.
的大小.
解法一:
(Ⅰ)取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]() ,
,
![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,
![]() .
.
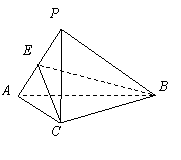 (Ⅱ)
(Ⅱ)![]() ,
,![]() ,
,
![]() .
.
又![]() ,
,
![]() .
.
又![]() ,即
,即
![]() ,且
,且![]() ,
,
![]() 平面
平面![]() .
.
取![]() 中点
中点![]() .连结
.连结![]() .
.
![]() ,
,![]() .
.
![]() 是
是![]() 在平面
在平面![]() 内的射影,
内的射影,![]() .
.
![]() 是二面角
是二面角![]() 的平面角.
的平面角.
在![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,
![]() .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
解法二:
(Ⅰ)![]() ,
,![]() ,
,![]() .
.
又![]() ,
,![]() .
.
![]() ,
,![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,
,![]() .
.
(Ⅱ)如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() .
.
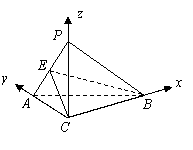 则
则![]() .
.
设![]() .
.
![]() ,
,
![]() ,
,![]() .取
.取![]() 中点
中点![]() ,连结
,连结![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 是二面角
是二面角![]() 的平面角.
的平面角.
![]() ,
,![]() ,
,![]() ,
,
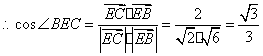 .
.
![]() 二面角
二面角![]() 的大小为
的大小为![]() .
.
21、(12分)为了了解《中华人民共和国道路交通安全法》在学生中的普及情况,调查部门对某校6名学生进行问卷调查.6人得分情况如下:
5,6,7,8,9,10.
把这6名学生的得分看成一个总体.
(Ⅰ)求该总体的平均数;
(Ⅱ)用简单随机抽样方法从这6名学生中抽取2名,他们的得分组成一个样本.求该样本平均数与总体平均数之差的绝对值不超过0.5的概率.
【解】:(Ⅰ)总体平均数为
![]() .··················································································· 4分
.··················································································· 4分
(Ⅱ)设![]() 表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”.
表示事件“样本平均数与总体平均数之差的绝对值不超过0.5”.
从总体中抽取2个个体全部可能的基本结果有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .共15个基本结果.
.共15个基本结果.
事件![]() 包括的基本结果有:
包括的基本结果有:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .共有7个基本结果.
.共有7个基本结果.
所以所求的概率为
![]() . 12分
. 12分
22、(12分)设函数![]() ,其中
,其中![]() .
.
(Ⅰ)当![]() 时,讨论函数
时,讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 仅在
仅在![]() 处有极值,求
处有极值,求![]() 的取值范围;
的取值范围;
(Ⅲ)若对于任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,求
上恒成立,求![]() 的取值范围.
的取值范围.
【解】(Ⅰ):![]() .
.
当![]() 时,
时,
![]() .
.
令![]() ,解得
,解得![]() ,
,![]() ,
,![]() .
.
当![]() 变化时,
变化时,![]() ,
,![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ↘ | 极小值 | ↗ | 极大值 | ↘ | 极小值 | ↗ |
所以![]() 在
在![]() ,
,![]() 内是增函数,在
内是增函数,在![]() ,
,![]() 内是减函数.
内是减函数.
(Ⅱ)![]() ,显然
,显然![]() 不是方程
不是方程![]() 的根.
的根.
为使![]() 仅在
仅在![]() 处有极值,必须
处有极值,必须![]() 恒成立,即有
恒成立,即有![]() .
.
解此不等式,得![]() .这时,
.这时,![]() 是唯一极值.
是唯一极值.
因此满足条件的![]() 的取值范围是
的取值范围是![]() .
.
(Ⅲ)由条件![]() 可知
可知![]() ,从而
,从而![]() 恒成立.当
恒成立.当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
因此函数![]() 在
在![]() 上的最大值是
上的最大值是![]() 与
与![]() 两者中的较大者.
两者中的较大者.
为使对任意的![]() ,不等式
,不等式![]() 在
在![]() 上恒成立,当且仅当
上恒成立,当且仅当![]() 即
即![]()
在![]() 上恒成立.
上恒成立.
所以![]() ,因此满足条件的
,因此满足条件的![]() 的取值范围是
的取值范围是![]() .
.