高三数学归纳法、极限、导数测试题
一、选择题：本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的．把答案填在答题卡相应位置上.
1.下列命题中，正确的是 （ ）
①数列
没有极限；②数列
的极限为0；
③数列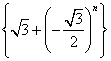
的极限为
；④数列
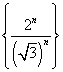没有极限
A. ①② B.①②③ C.②③④ D. ①②③④
2. 若
的值为 （ ）
A．－2 B．
C．
D．3
3.已知曲线
的一条切线的斜率为
，则切点的横坐标为 （
）
A. 1 B.2 C.3 D.4
4.若函数
在
内单调递减，则实数
的取值范围为（ ）
A. 
B.
C.
D.
5．设函数
，且
，则
（ ）
A．0 B． －1 C． 3 D．－6
6．函数
有极值的充要条件是（ ）
A．
B．
C．
D．
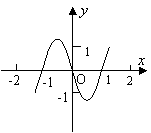
7．已知函数
的图象如右图所示（其中
是
函数
的导函数），下面四个图象中
的图
象大致是（ ）
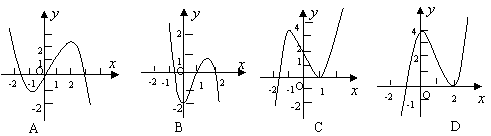
8．方程x3－6x2+9x－10=0的实根个数是 （ ）
A．3 B．2 C．1 D．0
9．若函数
在其定义域的一个子区间
上不是单调函数，则实数
的取值范围（ ）
A．
B．
C．
D．
10．设
、
是定义在
上的恒大于
的可导函数，且
，则当
时有（
）
A．
B．
C．
D．
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
班级 学号 姓名
二、填空题：本大题共5小题，每小题5分，共25分．把答案填在答题卡相应位置上．
11．曲线y=x3在点(1，1)处的切线与x轴、直线x=2所围成的三角形的面积为__________．
12． 若函数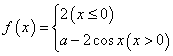
在上连续，则实数=______________
13．若函数
在
上有最大值，则实数的取值范围为_ __
14．过点
和曲线
相切的直线方程为_____
__
15．向高为8m，底面边长为8m的倒置正四棱锥形的容器内注水，其速度为每分钟
，则当水深为5m时，水面上升的速度为
．
三、解答题：本大题共6小题，共75分，解答应写出文字说明，证明过程或演算步骤．
16．（本题满分10分）设函数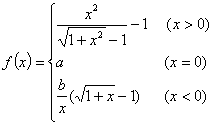
(1)若
在
处的极限存在，求
的值；
(2)若在处连续，求的值。
17．（本题满分12分）函数
，曲线
在点
处的切线平行于直线
,若函数
在
时有极值. (1)求,
的值；(2)求函数
的单调区间； (3) 若函数在区间
上的的最大值为10，求在该区间上的最小值.
18．（本题满分14分）已知数列
满足
，且
（1）用数学归纳法证明：
；
（2）若
，且
，求无穷数列
所有项的和
19．（本题满分12分）已知函数
（I）若函数在[0，2]上是单调递增函数，求a的取值范围；
（II）求函数在[0，2]上的最大值.
20．（本题满分12分）统计表明，某种型号的汽车在匀速行驶中每小时的耗油量
（升）关于行驶速度
（千米/小时）的函数解析式可以表示为：
．已知甲、乙两地相距100千米
（Ⅰ）当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地要耗油多少升？
（II）当汽车以多大的速度匀速行驶时，从甲地到乙地耗油最少？最少为多少升？
21．（本小题满分14分）设函数f（x）=
在[1，+∞
上为增函数。
（1）求正实数a的取值范围.
（2）若a=1，求证：
（n∈N*且n≥2）
宜昌市一中2008届高三《数学归纳法、极限、导数》测试题答案
DBAAB
CCCDC 11. 8/3 12. 4 13.
14. 
或
15. 8/75
16.（1）
（2）
17．(1) =2，,=-4
(2)函数的单调增区间为：（-∞，-2）（
，+∞）单调增区间为：（-2，）
(3) 由函数在区间上的的最大值为10，得c=2
在该区间上的最小值为：
18．
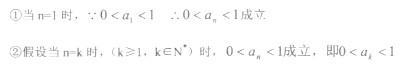
19．解：（1）
恒成立.
恒成立 
（2）①若
在[0，2]上是减函数，
②若
，则由（1）得：当
，此时在[0，2]上是减函数，
当
时，在[0，2]上是单调增函数，
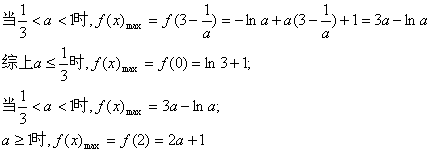
20．解：（I）当
时，汽车从甲地到乙地行驶了
小时，
要耗没
（升）。
答：当汽车以40千米/小时的速度匀速行驶时，从甲地到乙地耗油17.5升。
（II）当速度为千米/小时时，汽车从甲地到乙地行驶了
小时，设耗油量为
升，
依题意得
令
得
当
时，
是减函数；
当
时，
是增函数。 
当
时，取到极小值
因为在
上只有一个极值，所以它是最小值。
答汽车以80千米/小时的速度匀速行驶时，从甲地到乙地耗油最少，最少为11.25升。
21．解:（1）由已知：
=
依题意得：
≥0对x∈[1，+∞恒成立
∴ax－1≥0对x∈[1，+∞恒成立 ∴a－1≥0即：a≥1
（2）∵a=1 ∴由（1）知：f（x）=
在[1，+∞上为增函数，
∴n≥2时：f（
）=
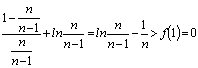
即：
…9分 ∴
设g（x）=lnx－x x∈[1，+∞， 则
对
恒成立，
∴g′（x）在[1+∞为减函数
∴n≥2时：g（）=ln－<g（1）=－1<0 即：ln<=1+（n≥2）
∴
综上所证：
（n∈N*且≥2）成立.