高三数学极坐标与参数方程单元练习1
一、选择题(每小题5分,共25分)
1、已知点M的极坐标为![]() ,下列所给出的四个坐标中能表示点M的坐标是( )。
,下列所给出的四个坐标中能表示点M的坐标是( )。
A. ![]() B.
B.
![]() C.
C.
![]() D.
D.
![]()
2、直线:3x-4y-9=0与圆:![]() ,(θ为参数)的位置关系是( )
,(θ为参数)的位置关系是( )
A.相切 B.相离 C.直线过圆心 D.相交但直线不过圆心
3、在参数方程![]() (t为参数)所表示的曲线上有B、C两点,它们对应的参数值分别为t1、t2,则线段BC的中点M对应的参数值是( )
(t为参数)所表示的曲线上有B、C两点,它们对应的参数值分别为t1、t2,则线段BC的中点M对应的参数值是( )
![]()
4、曲线的参数方程为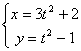 (t是参数),则曲线是( )
(t是参数),则曲线是( )
A、线段 B、双曲线的一支 C、圆 D、射线
5、实数x、y满足3x2+2y2=6x,则x2+y2的最大值为( )
A、![]() B、4 C、
B、4 C、![]() D、5
D、5
二、填空题(每小题5分,共30分)
1、点![]() 的极坐标为 。
的极坐标为 。
2、若A![]() ,B
,B![]() ,则AB=___________,
,则AB=___________,![]() ___________。(其中O是极点)
___________。(其中O是极点)
3、极点到直线![]() 的距离是________ _____。
的距离是________ _____。
4、极坐标方程![]() 表示的曲线是_______ _____。
表示的曲线是_______ _____。
5、圆锥曲线![]() 的准线方程是
。
的准线方程是
。
6、直线![]() 过点
过点![]() ,倾斜角是
,倾斜角是![]() ,且与直线
,且与直线![]() 交于
交于![]() ,则
,则![]() 的长为 。
的长为 。
三、解答题(第1题14分,第2题16分,第3题15分;共45分)
1、求圆心为C![]() ,半径为3的圆的极坐标方程。
,半径为3的圆的极坐标方程。
2、已知直线l经过点P(1,1),倾斜角![]() ,
,
(1)写出直线l的参数方程。
(2)设l与圆![]() 相交与两点A、B,求点P到A、B两点的距离之积。
相交与两点A、B,求点P到A、B两点的距离之积。
3、求椭圆![]()
![]() 。
。
极坐标与参数方程单元练习1参考答案
【试题答案】
一、选择题:1、D 2、D 3、B 4、D 5、B
二、填空题:1、![]() 或写成
或写成![]() 。 2、5,6。 3、
。 2、5,6。 3、![]() 。
。
4、![]() 5、
5、![]() 。
。
6、![]() 。
。
三、解答题
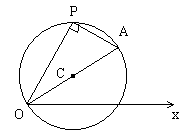
1、1、如下图,设圆上任一点为P(![]() ),则
),则![]()
![]()
![]() 而点O
而点O![]() A
A![]() 符合
符合
2、解:(1)直线的参数方程是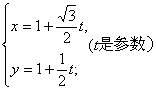
(2)因为点A,B都在直线l上,所以可设它们对应的参数为t1和t2,则点A,B的坐标分别为
![]()
![]()
以直线L的参数方程代入圆的方程![]() 整理得到
整理得到
![]() ①
①
因为t1和t2是方程①的解,从而t1t2=-2。
所以PA·PB= t1t2=-2=2。
3、(先设出点P的坐标,建立有关距离的函数关系)
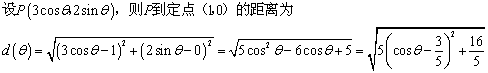
![]()
极坐标与参数方程单元练习2
1.已知点P的极坐标是(1,![]() ),则过点P且垂直极轴的直线极坐标方程是
.
),则过点P且垂直极轴的直线极坐标方程是
.
2.在极坐标系中,曲线![]() 一条对称轴的极坐标方程 .
一条对称轴的极坐标方程 .
3.在极坐标中,若过点(3,0)且与极轴垂直的直线交曲线![]() 于A、B两点.
于A、B两点.
则AB= .
4.已知三点A(5,![]() ),B(-8,
),B(-8,![]() ),C(3,
),C(3,![]() ),则ΔABC形状为 .
),则ΔABC形状为 .
5.已知某圆的极坐标方程为:ρ2 –4![]() ρcon(θ-π/4)+6=0
ρcon(θ-π/4)+6=0
则:①圆的普通方程 ;
②参数方程 ;
③圆上所有点(x,y)中xy的最大值和最小值分别为 、 .
6.设椭圆的参数方程为![]() ,
,![]() ,
,![]() 是椭圆上两点,
是椭圆上两点,
M、N对应的参数为![]() 且
且![]() ,则
,则![]() 大小关系是
.
大小关系是
.
7.直线:3x-4y-9=0与圆:![]() ,(θ为参数)的位置关系是
.
,(θ为参数)的位置关系是
.
8.经过点M0(1,5)且倾斜角为![]() 的直线,以定点M0到动 点P的位移t为参数的参数方程
的直线,以定点M0到动 点P的位移t为参数的参数方程
是 . 且与直线![]() 交于
交于![]() ,则
,则![]() 的长为
.
的长为
.
9.参数方程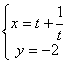 (t为参数)所表示的图形是 .
(t为参数)所表示的图形是 .
 10.方程
10.方程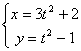 (t是参数)的普通方程是
.与x轴交点的直角坐标是
(t是参数)的普通方程是
.与x轴交点的直角坐标是
11.画出参数方程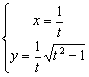 (
(![]() 为参数)所表示的曲线
为参数)所表示的曲线
.
12.已知动园:![]() ,
,
则圆心的轨迹是 .
13.已知过曲线![]() 上一点P,原点为O,直线PO的倾斜角
上一点P,原点为O,直线PO的倾斜角
为![]() ,则P点坐标是
.
,则P点坐标是
.
14.直线![]() (t为参数)上对应t=0, t=1两点间的距离是
.
(t为参数)上对应t=0, t=1两点间的距离是
.
15.直线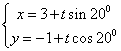 (t为参数)的倾斜角是
.
(t为参数)的倾斜角是
.
16.设![]() ,那么直线
,那么直线![]() 与圆
与圆![]() 的
的
位置关系是 .
17.直线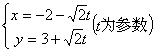 上与点
上与点![]() 距离等于
距离等于![]() 的点的坐标是
.
的点的坐标是
.
18.过抛物线y2=4x的焦点作倾斜角为![]() 的弦,若弦长不超过8,则
的弦,若弦长不超过8,则![]() 的取值范围是________________________________.
的取值范围是________________________________.
19.若动点(x,y)在曲线![]() (b>0)上变化,则x2 + 2y的最大值为 .
(b>0)上变化,则x2 + 2y的最大值为 .
20.曲线![]() (α为参数)与曲线
(α为参数)与曲线![]() (β为参数)的离心率分别为e1和e2,
(β为参数)的离心率分别为e1和e2,
则e1+e2的最小值为_______________.
极坐标与参数方程单元练习2参考答案
答案:1.ρcosθ= -1;2.![]() ;3.
;3.![]() ;4.等边三角形;5.(x-2)2+(y-2)2=2;
;4.等边三角形;5.(x-2)2+(y-2)2=2;
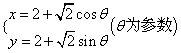 ;9、1;6.θ1>θ2;7.相交;8.
;9、1;6.θ1>θ2;7.相交;8. 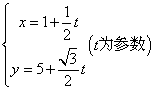
10+6![]() ;9.两条射线;10.x-3y=5(x≥2);(5, 0);12.椭圆;13.
;9.两条射线;10.x-3y=5(x≥2);(5, 0);12.椭圆;13.![]() ;14.
;14.![]() ;
;
15.700;16.相切;17.(-1,2)或(-3,4);18.![]() ;19.
;19.![]() ;20.
;20.![]()
极坐标与参数方程单元练习3
一.选择题(每题5分共60分)
1.设椭圆的参数方程为![]() ,
,![]() ,
,![]() 是椭圆上两点,M,N对应的参数为
是椭圆上两点,M,N对应的参数为![]() 且
且![]() ,则
,则
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.直线:3x-4y-9=0与圆:![]() ,(θ为参数)的位置关系是( )
,(θ为参数)的位置关系是( )
A.相切 B.相离 C.直线过圆心 D.相交但直线不过圆心
3.经过点M(1,5)且倾斜角为![]() 的直线,以定点M到动 点P的位移t为参数的参数方程是( )
的直线,以定点M到动 点P的位移t为参数的参数方程是( )
A.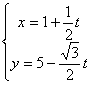 B.
B. 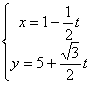 C.
C. 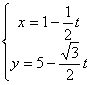 D.
D. 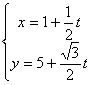
4.参数方程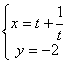 (t为参数)所表示的曲线是 ( )
(t为参数)所表示的曲线是 ( )
A.一条射线 B.两条射线 C.一条直线 D.两条直线
5.若动点(x,y)在曲线![]() (b>0)上变化,则x2+2y的最大值为
(b>0)上变化,则x2+2y的最大值为
(A) 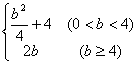 ; (B)
; (B) 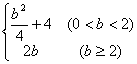 ;(C)
;(C) ![]() (D) 2b。
(D) 2b。
6.实数x、y满足3x2+2y2=6x,则x2+y2的最大值为( )
A、![]() B、4 C、
B、4 C、![]() D、5
D、5
7.曲线的参数方程为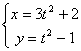 (t是参数),则曲线是
(t是参数),则曲线是
A、线段 B、双曲线的一支 C、圆 D、射线
8. 已知动园:![]() ,则圆心的轨迹是
,则圆心的轨迹是
A、直线 B、圆 C、抛物线的一部分 D、椭圆
9. 在参数方程![]() (t为参数)所表示的曲线上有B、C两点,它们对应的参数值分别为t1、t2,则线段BC的中点M对应的参数值是
(t为参数)所表示的曲线上有B、C两点,它们对应的参数值分别为t1、t2,则线段BC的中点M对应的参数值是
![]()
10.设![]() ,那么直线
,那么直线![]() 与圆
与圆![]() 的位置关系是
的位置关系是
A、相交 B、相切 C、相离 D、视![]() 的大小而定
的大小而定
11. 下列参数方程(t为参数)中与普通方程x2-y=0表示同一曲线的是
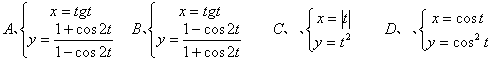
12.已知过曲线![]() 上一点P,原点为O,直线PO的倾斜角为
上一点P,原点为O,直线PO的倾斜角为![]() ,则P点坐标是
,则P点坐标是
A、(3,4) B、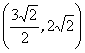 C、(-3,-4) D、
C、(-3,-4) D、![]()
二.填空题(每题5分共25分)
13.过抛物线y2=4x的焦点作倾斜角为![]() 的弦,若弦长不超过8,则
的弦,若弦长不超过8,则![]() 的取值范围是________________________________。
的取值范围是________________________________。
14.直线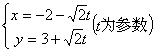 上与点
上与点![]() 距离等于
距离等于![]() 的点的坐标是
的点的坐标是
15.圆锥曲线![]() 的准线方程是
的准线方程是
16.直线![]() 过点
过点![]() ,倾斜角是
,倾斜角是![]() ,且与直线
,且与直线![]() 交于
交于![]() ,则
,则![]() 的长为
的长为
17.曲线![]() (α为参数)与曲线
(α为参数)与曲线![]() (β为参数)的离心率分别为e1和e2,则e1+e2的最小值为_______________.
(β为参数)的离心率分别为e1和e2,则e1+e2的最小值为_______________.
三.解答题(共65分
18.
19.已知方程![]() 。
。
(1)试证:不论![]() 如何变化,方程都表示顶点在同一椭圆上的抛物线;
如何变化,方程都表示顶点在同一椭圆上的抛物线;
(2)![]() 为何值时,该抛物线在直线x=14上截得的弦最长?并求出此弦长。
为何值时,该抛物线在直线x=14上截得的弦最长?并求出此弦长。
20.已知椭圆![]() 上两个相邻顶点为A、C,又B、D为椭圆上的两个动点,且B、D分别在直线AC的两旁,求四边形ABCD面积的最大值。
上两个相邻顶点为A、C,又B、D为椭圆上的两个动点,且B、D分别在直线AC的两旁,求四边形ABCD面积的最大值。
21.已知过点P(1,-2),倾斜角为![]() 的直线l和抛物线x2=y+m
的直线l和抛物线x2=y+m
(1)m取何值时,直线l和抛物线交于两点?
(2)m取何值时,直线l被抛物线截下的线段长为![]() .
.
极坐标与参数方程单元练习3参考答案
答案
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 | B | D | A | B | A | B | D | D | B | B | D | D |
13.![]() ;14.
;14.![]() ; 15.
; 15.![]() ;16.
;16.![]() ;17.
;17.![]()
18.解:把直线参数方程化为标准参数方程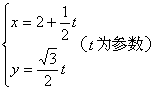
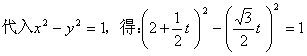
![]()
![]()
![]()
![]()
19(1)把原方程化为![]() ,知抛物线的顶点为
,知抛物线的顶点为![]() 它是在椭圆
它是在椭圆![]() 上;(2)当
上;(2)当![]() 时,弦长最大为12。
时,弦长最大为12。
20、![]()
21.(1)m>![]() ,(2)m=3
,(2)m=3
极坐标与参数方程单元练习4
(一)选择题:
 [ ]
[ ]
A.(2,-7) B.(1,0)
![]()

A.20° B.70° C.110° D.160°
 [ ]
[ ]
A.相切 B.相离 C.直线过圆心 D.相交但直线不过圆心

A.椭圆 B.双曲线 C.抛物线 D.圆
![]() [ ]
[ ]
![]()
C.5 D.6
(二)填空题:

8.设y=tx(t为参数),则圆x2+y2-4y=0的参数方程是______.
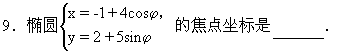
10.当m取一切实数时,双曲线x2-y2-6mx-4my+5m2-1=0的中心的轨迹方程为______.
(三)解答题:
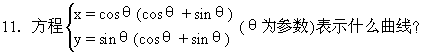
![]()
时矩形对角线的倾斜角α.
13.直线l经过两点 P(-1,2)和Q(2,-2),与双曲线(y-2)2-x2=1相交于两点A、B,
(1)根据下问所需写出l的参数方程;
(2)求AB中点M与点P的距离.
14.设椭圆4x2+y2=1的平行弦的斜率为2,求这组平行弦中点的轨迹.
15.若不计空气阻力,炮弹运行轨道是抛物线.现测得我炮位A与炮击目标B在同一水平线上,水平距离为6000米,炮弹运行的最大高度为1200米.试求炮弹的发射角α和发射初速度v0(重力加速度g=9.8米/秒2).
极坐标与参数方程单元练习4参考答案
(一)1.C 2.C 3.D 4.B 5.A
(二)6.(1,0),(-5,0)
7.4x2-y2=16(x≥2)
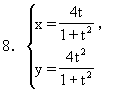
9.(-1,5),(-1,-1)
10.2x+3y=0
(三)11.圆x2+y2-x-y=0.
![]()
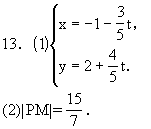
14.取平行弦中的一条弦AB在y轴上的截距m为参数,并设A(x1,
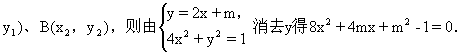
![]()
![]()
设弦AB的中点为M(x,y),则
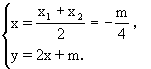

15.在以A为原点,直线AB的x轴的直角坐标系中,弹道方程是
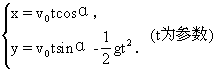
它经过最高点(3000,1200)和点B(6000,0)的时间分别设为t0和2t0,代入参数方程,得
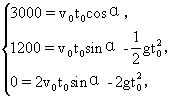
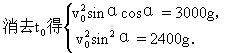
![]()
极坐标与参数方程单元练习5
一.选择题(每题5分共50分)
1.已知![]() ,下列所给出的不能表示点的坐标的是
,下列所给出的不能表示点的坐标的是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.点![]() ,则它的极坐标是
,则它的极坐标是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.极坐标方程![]() 表示的曲线是
表示的曲线是
A.双曲线 B.椭圆 C.抛物线 D.圆
4.圆![]() 的圆心坐标是
的圆心坐标是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.在极坐标系中,与圆![]() 相切的一条直线方程为
相切的一条直线方程为
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6、 已知点![]() 则
则![]() 为
为
A、正三角形 B、直角三角形 C、锐角等腰三角形 D、直角等腰三角形
7、![]() 表示的图形是
表示的图形是
A.一条射线 B.一条直线 C.一条线段 D.圆
8、直线![]() 与
与![]() 的位置关系是
的位置关系是
A、平行 B、垂直 C、相交不垂直 D、与![]() 有关,不确定
有关,不确定
9.两圆![]() ,
,![]() 的公共部分面积是
的公共部分面积是
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
10.已知点![]() 的球坐标是
的球坐标是![]() ,
,![]() 的柱坐标是
的柱坐标是![]() ,求
,求![]() .
.
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二.填空题(每题5分共25分)
11.极坐标方程![]() 化为直角坐标方程是
化为直角坐标方程是
12.圆心为![]() ,半径为3的圆的极坐标方程为
,半径为3的圆的极坐标方程为
13.已知直线的极坐标方程为![]() ,则极点到直线的距离是
,则极点到直线的距离是
14、在极坐标系中,点P![]() 到直线
到直线![]() 的距离等于____________。
的距离等于____________。
15、与曲线![]() 关于
关于![]() 对称的曲线的极坐标方程是________________________。
对称的曲线的极坐标方程是________________________。
三.解答题(共75分)
16.说说由曲线![]() 得到曲线
得到曲线![]() 的变化过程,并求出坐标伸缩变换。(7分)
的变化过程,并求出坐标伸缩变换。(7分)
17.已知![]() ,O为极点,求使
,O为极点,求使![]() 是正三角形的
是正三角形的![]() 点坐标。(8分)
点坐标。(8分)
18.棱长为1的正方体![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点P,顶点O为坐标原点,OA、OC分别在
相交于点P,顶点O为坐标原点,OA、OC分别在![]() 的正半轴上,已知点P的球坐标
的正半轴上,已知点P的球坐标![]() ,求
,求![]() 。(10分)
。(10分)
19.![]() 的底边
的底边![]() 以B点为极点,BC 为极轴,求顶点A 的轨迹方程。(10分)
以B点为极点,BC 为极轴,求顶点A 的轨迹方程。(10分)
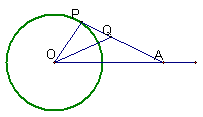 20.在平面直角坐标系中已知点A(3,0),P是圆珠笔
20.在平面直角坐标系中已知点A(3,0),P是圆珠笔![]() 上一个运点,且
上一个运点,且![]() 的平分线交PA于Q点,求Q 点的轨迹的极坐标方程。
的平分线交PA于Q点,求Q 点的轨迹的极坐标方程。
(10分)
21、在极坐标系中,已知圆C的圆心C![]() ,半径
,半径![]() =1,Q点在圆C上运动。
=1,Q点在圆C上运动。
(1)求圆C的极坐标方程;
(2)若P在直线OQ上运动,且OQ∶QP=2∶3,求动点P的轨迹方程。(10分)
22、建立极坐标系证明:已知半圆直径∣AB∣=2![]() (
(![]() >0),半圆外一条直线
>0),半圆外一条直线![]() 与AB所在直线垂直相交于点T,并且∣AT∣=2
与AB所在直线垂直相交于点T,并且∣AT∣=2![]() 。若半圆上相异两点M、N到
。若半圆上相异两点M、N到![]() 的距离∣MP∣,∣NQ∣满足∣MP∣∶∣MA∣=∣NQ∣∶∣NA∣=1,则 ∣MA∣+∣NA∣=∣AB∣。
的距离∣MP∣,∣NQ∣满足∣MP∣∶∣MA∣=∣NQ∣∶∣NA∣=1,则 ∣MA∣+∣NA∣=∣AB∣。
(10分)
23.如图,![]() ,D是垂足,H是AD上任意一点,直线BH与AC交于E点,直线CH与AB交于F点,求证:
,D是垂足,H是AD上任意一点,直线BH与AC交于E点,直线CH与AB交于F点,求证:![]() (10分)
(10分)
极坐标与参数方程单元练习5参考答案
答案
一.选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | A | C | D | A | B | D | A | B | C | A |
二.填空题
11.![]() ;12.
;12.![]() ;13.
;13.![]() ; 14.
; 14.![]() ;15.
;15. ![]()
三.解答题
16.解:![]() 的图象上的点的纵坐标不变,横坐标缩短为原来的
的图象上的点的纵坐标不变,横坐标缩短为原来的![]() ,得到
,得到![]() ,再将其纵坐标伸长为原来的3倍,横坐标不变,得到曲线
,再将其纵坐标伸长为原来的3倍,横坐标不变,得到曲线![]() 。
。
设![]() ,变换公式为
,变换公式为
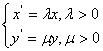
将其代入![]() 得
得
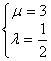 ,
,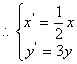
17.![]() 或
或![]()
18.![]()
19.解:设![]() 是曲线上任意一点,在
是曲线上任意一点,在![]()
中由正弦定理得: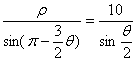
得A的轨迹是:![]()
20.解:以O为极点,![]() 轴正半轴为极轴建立极坐标系,设
轴正半轴为极轴建立极坐标系,设![]() ,
,![]()
![]()
![]()
![]()
21.(1)![]()
(2)![]()
22.证法一:以A为极点,射线AB为极轴建立直角坐标系,则半圆的的极坐标方程为![]() ,设
,设![]() ,则
,则![]() ,
,![]() ,又
,又![]() ,
,![]() ,
,
![]()
![]()
![]() 是方程
是方程![]() 的两个根,由韦达定理:
的两个根,由韦达定理:![]() ,
,![]()
证法二:以A为极点,射线AB为极轴建立直角坐标系,则半圆的的极坐标方程为![]() ,设
,设![]()
又由题意知,![]() 在抛物线
在抛物线![]() 上,
上,![]() ,
,![]() ,
,![]() 是方程
是方程![]() 的两个根,由韦达定理:
的两个根,由韦达定理:![]() ,
,![]()
 23.证明:以BC所在的直线为
23.证明:以BC所在的直线为![]() 轴,AD所在的直线为
轴,AD所在的直线为![]() 轴建立直角坐标系,设
轴建立直角坐标系,设![]() ,
,![]() ,
,![]() ,
,![]() ,则
,则
![]() ,即
,即![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
![]() ,即
,即![]()
![]() ,
,![]()
![]()
![]()
![]()
![]()
坐标系与参数方程单元练习6
一、选择题
1.若直线的参数方程为![]() ,则直线的斜率为( )
,则直线的斜率为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
2.下列在曲线![]() 上的点是( )
上的点是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
3.将参数方程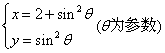 化为普通方程为( )
化为普通方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.化极坐标方程![]() 为直角坐标方程为( )
为直角坐标方程为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.点![]() 的直角坐标是
的直角坐标是![]() ,则点
,则点![]() 的极坐标为( )
的极坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
6.极坐标方程![]() 表示的曲线为( )
表示的曲线为( )
A.一条射线和一个圆 B.两条直线 C.一条直线和一个圆 D.一个圆
二、填空题
1.直线![]() 的斜率为______________________。
的斜率为______________________。
2.参数方程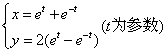 的普通方程为__________________。
的普通方程为__________________。
3.已知直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,又点
,又点![]() ,
,
则![]() _______________。
_______________。
4.直线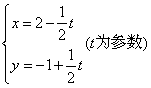 被圆
被圆![]() 截得的弦长为______________。
截得的弦长为______________。
5.直线![]() 的极坐标方程为____________________。
的极坐标方程为____________________。
三、解答题
1.已知点![]() 是圆
是圆![]() 上的动点,
上的动点,
(1)求![]() 的取值范围;
的取值范围;
(2)若![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围。
的取值范围。
2.求直线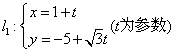 和直线
和直线![]() 的交点
的交点![]() 的坐标,及点
的坐标,及点![]()
与![]() 的距离。
的距离。
3.在椭圆![]() 上找一点,使这一点到直线
上找一点,使这一点到直线![]() 的距离的最小值。
的距离的最小值。
坐标系与参数方程单元练习6参考答案
一、选择题
1.D ![]()
2.B 转化为普通方程:![]() ,当
,当![]() 时,
时,![]()
3.C 转化为普通方程:![]() ,但是
,但是![]()
4.C ![]()
5.C ![]() 都是极坐标
都是极坐标
6.C ![]()
则![]() 或
或![]()
二、填空题
1.![]()
![]()
2.![]()
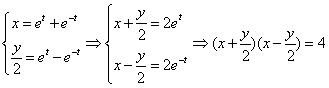
3.![]() 将
将![]() 代入
代入![]() 得
得![]() ,则
,则![]() ,而
,而![]() ,得
,得![]()
4.![]() 直线为
直线为![]() ,圆心到直线的距离
,圆心到直线的距离![]() ,弦长的一半为
,弦长的一半为![]() ,得弦长为
,得弦长为![]()
5.![]()
![]() ,取
,取![]()
三、解答题
1.解:(1)设圆的参数方程为![]() ,
,
![]()
![]()
(2)![]()
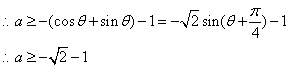
2.解:将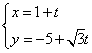 代入
代入![]() 得
得![]() ,
,
得![]() ,而
,而![]() ,得
,得![]()
3.解:设椭圆的参数方程为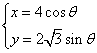 ,
,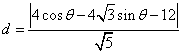
![]()
当![]() 时,
时,![]() ,此时所求点为
,此时所求点为![]() 。
。
坐标系与参数方程单元练习7
一、选择题
1.直线![]() 的参数方程为
的参数方程为![]() ,
,![]() 上的点
上的点![]() 对应的参数是
对应的参数是![]() ,则点
,则点![]() 与
与![]() 之间的距离是( )
之间的距离是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
2.参数方程为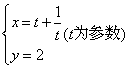 表示的曲线是( )
表示的曲线是( )
A.一条直线 B.两条直线 C.一条射线 D.两条射线
3.直线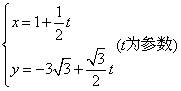 和圆
和圆![]() 交于
交于![]() 两点,
两点,
则![]() 的中点坐标为( )
的中点坐标为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4.圆![]() 的圆心坐标是( )
的圆心坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5.与参数方程为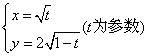 等价的普通方程为( )
等价的普通方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
6.直线![]() 被圆
被圆![]() 所截得的弦长为( )
所截得的弦长为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题
1.曲线的参数方程是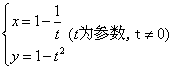 ,则它的普通方程为__________________。
,则它的普通方程为__________________。
2.直线![]() 过定点_____________。
过定点_____________。
3.点![]() 是椭圆
是椭圆![]() 上的一个动点,则
上的一个动点,则![]() 的最大值为___________。
的最大值为___________。
4.曲线的极坐标方程为![]() ,则曲线的直角坐标方程为________________。
,则曲线的直角坐标方程为________________。
5.设![]() 则圆
则圆![]() 的参数方程为__________________________。
的参数方程为__________________________。
三、解答题
1.参数方程![]() 表示什么曲线?
表示什么曲线?
2.点![]() 在椭圆
在椭圆![]() 上,求点
上,求点![]() 到直线
到直线![]() 的最大距离和最小距离。
的最大距离和最小距离。
3.已知直线![]() 经过点
经过点![]() ,倾斜角
,倾斜角![]() ,
,
(1)写出直线![]() 的参数方程。
的参数方程。
(2)设![]() 与圆
与圆![]() 相交与两点
相交与两点![]() ,求点
,求点![]() 到
到![]() 两点的距离之积。
两点的距离之积。
坐标系与参数方程单元练习7参考答案
一、选择题
1.C 距离为![]()
2.D ![]() 表示一条平行于
表示一条平行于![]() 轴的直线,而
轴的直线,而![]() ,所以表示两条射线
,所以表示两条射线
3.D ![]() ,得
,得![]() ,
,![]()
中点为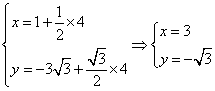
4.A 圆心为![]()
5.D ![]()
6.C 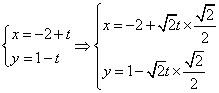 ,把直线
,把直线![]() 代入
代入
![]() 得
得![]()
![]() ,弦长为
,弦长为![]()
二、填空题
1.![]()
![]() 而
而![]() ,
,
即![]()
2.![]()
![]() ,
,![]() 对于任何
对于任何![]() 都成立,则
都成立,则![]()
3.![]() 椭圆为
椭圆为![]() ,设
,设![]() ,
,
![]()
4.![]()
![]() 即
即![]()
5.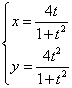
![]() ,当
,当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
而![]() ,即
,即![]() ,得
,得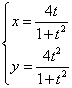
三、解答题
1.解:显然![]() ,则
,则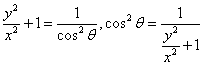
![]()
即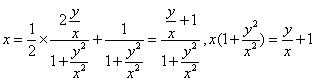
得![]() ,即
,即![]()
2.解:设![]() ,则
,则![]()
即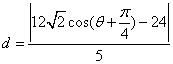 ,
,
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() 。
。
3.解:(1)直线的参数方程为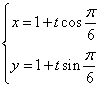 ,即
,即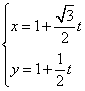
(2)把直线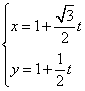 代入
代入![]()
得![]()
![]() ,则点
,则点![]() 到
到![]() 两点的距离之积为
两点的距离之积为![]()
坐标系与参数方程单元练习8
一、选择题
1.把方程![]() 化为以
化为以![]() 参数的参数方程是( )
参数的参数方程是( )
A.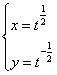 B.
B.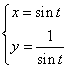 C.
C.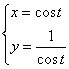 D.
D.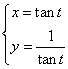
2.曲线![]() 与坐标轴的交点是( )
与坐标轴的交点是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
3.直线![]() 被圆
被圆![]() 截得的弦长为( )
截得的弦长为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
4.若点![]() 在以点
在以点![]() 为焦点的抛物线
为焦点的抛物线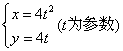 上,
上,
则![]() 等于( )
等于( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
5.极坐标方程![]() 表示的曲线为( )
表示的曲线为( )
A.极点 B.极轴
C.一条直线 D.两条相交直线
6.在极坐标系中与圆![]() 相切的一条直线的方程为( )
相切的一条直线的方程为( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
二、填空题
1.已知曲线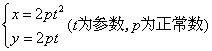 上的两点
上的两点![]() 对应的参数分别为
对应的参数分别为![]() ,
,![]() ,那么
,那么![]() =_______________。
=_______________。
2.直线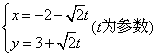 上与点
上与点![]() 的距离等于
的距离等于![]() 的点的坐标是_______。
的点的坐标是_______。
3.圆的参数方程为![]() ,则此圆的半径为_______________。
,则此圆的半径为_______________。
4.极坐标方程分别为![]() 与
与![]() 的两个圆的圆心距为_____________。
的两个圆的圆心距为_____________。
5.直线![]() 与圆
与圆![]() 相切,则
相切,则![]() _______________。
_______________。
三、解答题
1.分别在下列两种情况下,把参数方程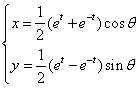 化为普通方程:
化为普通方程:
(1)![]() 为参数,
为参数,![]() 为常数;(2)
为常数;(2)![]() 为参数,
为参数,![]() 为常数;
为常数;
2.过点![]() 作倾斜角为
作倾斜角为![]() 的直线与曲线
的直线与曲线![]() 交于点
交于点![]() ,
,
求![]() 的最小值及相应的
的最小值及相应的![]() 的值。
的值。
坐标系与参数方程单元练习8参考答案
一、选择题
1.D ![]() ,
,![]() 取非零实数,而A,B,C中的
取非零实数,而A,B,C中的![]() 的范围有各自的限制
的范围有各自的限制
2.B 当![]() 时,
时,![]() ,而
,而![]() ,即
,即![]() ,得与
,得与![]() 轴的交点为
轴的交点为![]() ;
;
当![]() 时,
时,![]() ,而
,而![]() ,即
,即![]() ,得与
,得与![]() 轴的交点为
轴的交点为![]()
3.B 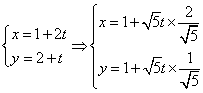 ,把直线
,把直线![]() 代入
代入
![]() 得
得![]()
![]() ,弦长为
,弦长为![]()
4.C 抛物线为![]() ,准线为
,准线为![]() ,
,![]() 为
为![]() 到准线
到准线![]() 的距离,即为
的距离,即为![]()
5.D ![]() ,为两条相交直线
,为两条相交直线
6.A ![]() 的普通方程为
的普通方程为![]() ,
,![]() 的普通方程为
的普通方程为![]()
圆![]() 与直线
与直线![]() 显然相切
显然相切
二、填空题
1.![]() 显然线段
显然线段![]() 垂直于抛物线的对称轴。即
垂直于抛物线的对称轴。即![]() 轴,
轴,![]()
2.![]() ,或
,或![]()
![]()
3.![]() 由
由![]() 得
得![]()
4.![]() 圆心分别为
圆心分别为![]() 和
和![]()
5.![]() ,或
,或![]() 直线为
直线为![]() ,圆为
,圆为![]() ,作出图形,相切时,
,作出图形,相切时,
易知倾斜角为![]() ,或
,或![]()
三、解答题
1.解:(1)当![]() 时,
时,![]() ,即
,即![]() ;
;
当![]() 时,
时,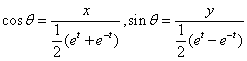
而![]() ,即
,即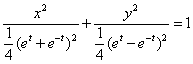
(2)当![]() 时,
时,![]() ,
,![]() ,即
,即![]() ;
;
当![]() 时,
时,![]() ,
,![]() ,即
,即![]() ;
;
当![]() 时,得
时,得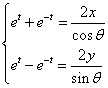 ,即
,即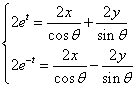
得![]()
即![]() 。
。
2.解:设直线为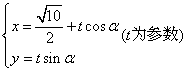 ,代入曲线并整理得
,代入曲线并整理得
![]()
则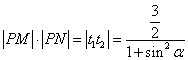
所以当![]() 时,即
时,即![]() ,
,![]() 的最小值为
的最小值为![]() ,此时
,此时![]() 。
。