高三数学立几、概率统计、导数、集合月考检测卷14.5.13
选编:徐良云
一、选择题(5′×12=60′)
1、若![]() 是平面
是平面![]() 外一点,则下列命题正确的是( D
)
外一点,则下列命题正确的是( D
)
A.过![]() 只能作一条直线与平面
只能作一条直线与平面![]() 相交
B.过
相交
B.过![]() 可作无数条直线与平面
可作无数条直线与平面![]() 垂直
垂直
C.过![]() 只能作一条直线与平面
只能作一条直线与平面![]() 平行
D.过
平行
D.过![]() 可作无数条直线与平面
可作无数条直线与平面![]() 平行
平行
2、已知曲线![]() 的一条切线的斜率为
的一条切线的斜率为![]() ,则切点的横坐标为( A )
,则切点的横坐标为( A )
A.1 B.2 C.3 D.4
3、某一批花生种子,如果每1粒发芽的概率为![]() ,那么播下3粒种子恰有2粒发芽的概率是( C )
,那么播下3粒种子恰有2粒发芽的概率是( C )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
4、曲线![]() 在点
在点![]() 处的切线的倾斜角为( B )
处的切线的倾斜角为( B )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
5、![]() 在区间
在区间![]() 上的最大值是( C )
上的最大值是( C )
A.![]() B.
B.![]() C.2
D.4
C.2
D.4
6、设曲线![]() 在点(1,
在点(1,![]() )处的切线与直线
)处的切线与直线![]() 平行,则
平行,则![]() ( A )
( A )
A.1
B.![]() C.
C.![]() D.
D.![]()
7、袋中有40个小球,其中红色球16个、蓝色球12个、白色球8个、黄色球4个,从中随机抽取10个球作成一个样本,则这个样本恰好是按分层抽样方法得到的概率为( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
8、从4名男生和3名女生中选出3人,分别从事三项不同的工作,若这3人中至少有1名女生,则选派方案共有( B )
A.108种 B.186种 C.216种 D.270种
9、设![]() 在
在![]() 内单调递增,
内单调递增,![]() ,则
,则![]() 是
是![]() 的( C )
的( C )
A.充分不必要条件 B.必要不充分条件
C.充分必要条件 D.既不充分也不必要条件
10、曲线![]() 在点
在点![]() 处的切线与坐标轴围成的三角形面积为( A )
处的切线与坐标轴围成的三角形面积为( A )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
11、已知对任意实数![]() ,有
,有![]() ,
,![]() ,且
,且![]() 时,
时,![]() ,
,![]() ,则
,则![]() 时( B )
时( B )
A.![]() ,
,![]() B.
B.![]() ,
,![]()
C.![]() ,
,![]() D.
D.![]() ,
,![]()
12、过点![]() 作抛物线
作抛物线![]() 的切线,则其中一条切线为( D )
的切线,则其中一条切线为( D )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
二、填空题(5′×4=20′)
13、![]() 的展开式中常数项为 ;各项系数之和为 .(用数字作答)
的展开式中常数项为 ;各项系数之和为 .(用数字作答)
【答案】10 32
14、函数![]() 是减函数的区间为 .
是减函数的区间为 .
【答案】![]()
 15、已知函数
15、已知函数![]() ,
,![]() .
.
答案:-2
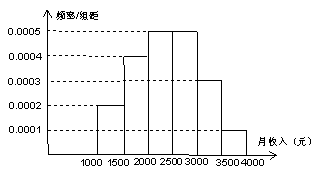
16、一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图)。为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在![]() (元)月收入段应抽出__25__人.
(元)月收入段应抽出__25__人.
三、解答题(共6小题,计70分。解答应写出文字说明,证明过程或演算步骤。)
17、设![]() ,
,![]() ,
,![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
解:![]()
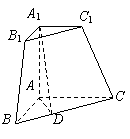
18、三棱锥被平行于底面![]() 的平面所截得的几何体如图所示,截面为
的平面所截得的几何体如图所示,截面为![]() ,
,![]() ,
,![]() 平面
平面![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
 (1)证明:平面
(1)证明:平面![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小.
的大小.
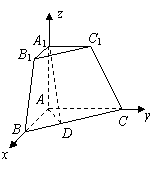
解:(Ⅰ)如图,建立空间直角坐标系,
 则
则![]() ,
,
![]() ,
,![]() .
.
![]() 点坐标为
点坐标为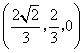 .
.
![]()
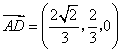 ,
,![]() .
.
![]() ,
,![]() ,
,![]() ,
,![]() ,又
,又![]() ,
,
![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() ,
,![]() 平面
平面![]() 平面
平面![]() .
.
(Ⅱ)![]() 平面
平面![]() ,取
,取![]() 为平面
为平面![]() 的法向量,
的法向量,
设平面![]() 的法向量为
的法向量为![]() ,则
,则![]() .
.
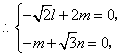
![]() ,如图,可取
,如图,可取![]() ,则
,则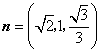 ,
,
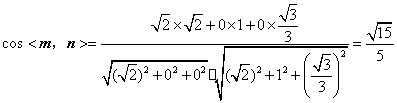 ,
,
即二面角![]() 为
为![]() .
.
19、在某次普通话测试中,为测试汉字发音水平,设置了10张卡片,每张卡片印有一个汉字的拼音,其中恰有3张卡片上的拼音带有后鼻音“g”,
(1)现对三位被测试者先后进行测试,第一位被测试者从这10张卡片总随机抽取1张,测试后放回,余下2位的测试,也按同样的方法进行。求这三位被测试者抽取的卡片上,拼音都带有后鼻音“g”的概率;
(2)若某位被测试者从10张卡片中一次随机抽取3张,求这三张卡片上,拼音带有后鼻音“g”的卡片不少于2张的概率.
解:(1)每次测试中,被测试者从10张卡片中随机抽取1张卡片上,拼音带有后鼻音“g”的概率为![]() ,因为三位被测试者分别随机抽取一张卡片的事件是相互独立的,因而所求的概率为
,因为三位被测试者分别随机抽取一张卡片的事件是相互独立的,因而所求的概率为![]()
(2)设![]() 表示所抽取的三张卡片中,恰有
表示所抽取的三张卡片中,恰有![]() 张卡片带有后鼻音“g”的事件,且其相应的概率为
张卡片带有后鼻音“g”的事件,且其相应的概率为![]() 则
则![]() ,
, ![]()
因而所求概率为![]()
20、用长为18 cm的钢条围成一个长方体形状的框架,要求长方体的长与宽之比为2:1,问该长方体的长、宽、高各为多少时,其体积最大?最大体积是多少?
解:设长方体的宽为x(m),则长为2x(m),高为
![]() .
.
故长方体的体积为![]()
从而![]()
令V′(x)=0,解得x=0(舍去)或x=1,因此x=1.
当0<x<1时,V′(x)>0;当1<x<![]() 时,V′(x)<0,
时,V′(x)<0,
故在x=1处V(x)取得极大值,并且这个极大值就是V(x)的最大值。
从而最大体积V=V′(x)=9×12-6×13(m3),此时长方体的长为2 m,高为1.5 m.
答:当长方体的长为2 m时,宽为1 m,高为1.5 m时,体积最大,最大体积为3 m3。
21、(07全国1) 设函数![]() 在
在![]() 及
及![]() 时取得极值,
时取得极值,
(1)求![]() 、
、![]() 的值;
的值;
(2)若对任意的![]() ,都有
,都有![]() 成立,求c的取值范围.
成立,求c的取值范围.
解:(Ⅰ)![]() ,
,
因为函数![]() 在
在![]() 及
及![]() 取得极值,则有
取得极值,则有![]() ,
,![]() .
.
即![]() 解得
解得![]() ,
,![]() .
.
(Ⅱ)由(Ⅰ)可知,![]() ,
,
![]() .当
.当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
所以,当![]() 时,
时,![]() 取得极大值
取得极大值![]() ,又
,又![]() ,
,![]() .
.
则当![]() 时,
时,![]() 的最大值为
的最大值为![]() .
.
因为对于任意的![]() ,有
,有![]() 恒成立,所以
恒成立,所以 ![]() ,
,
解得 ![]() 或
或![]() ,因此
,因此![]() 的取值范围为
的取值范围为![]() .
.
22、已知函数![]() ,
,
(1)若![]() 在实数集
在实数集![]() 上单调递增,求实数
上单调递增,求实数![]() 的取值范围;
的取值范围;
(2)是否存在实数![]() ,使
,使![]() 在
在![]() 上单调递减?若存在,求出
上单调递减?若存在,求出![]() 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
解:(1)![]() (2)
(2)![]()